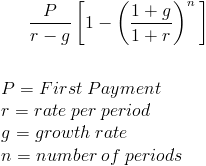
nuvärdet av en växande livränta formel beräknar nuvärdet av en serie framtida periodiska betalningar som växer i proportionerlig takt. En växande livränta kan ibland kallas en ökande livränta. Ett enkelt exempel på en växande livränta skulle vara en person som får $100 det första året och successiva betalningar ökar med 10% per år under totalt tre år. Detta skulle vara ett kvitto på $100, $110 respektive $121.
nuvärdet av en växande livränta formel bygger på begreppet tidsvärde av pengar. Utgångspunkten för detta koncept är att en viss mängd pengar är värt mer idag än vid en framtida tidpunkt.liksom alla finansiella formler som involverar en ränta är det viktigt att korrelera räntan per period till antalet perioder i nuvärdet av en växande livränta formel. Om betalningarna är månatliga, skulle räntan behöva vara månadsavgiften.
hur är nuvärdet av en växande livränta härledd?
nuvärdet av en växande livränta är summan av framtida kassaflöden. För en växande livränta ökar varje kassaflöde i en viss takt. Formeln för nuvärdet av en växande livränta kan skrivas som
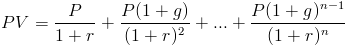
denna formel är den allmänna formeln för att summera de diskonterade framtida kassaflödena tillsammans med att använda 1 + g till faktor i att varje framtida kassaflöde kommer att öka till en viss takt.
detta nuvärde av en växande livränta formel kan sedan skrivas om som
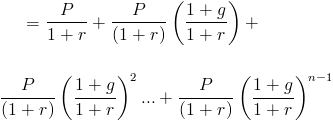
detta skulle betraktas som en geometrisk serie där (1+g)/(1+r) är det gemensamma förhållandet. Genom att använda den geometriska serieformeln visas nuvärdet för en växande livränta som
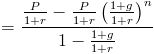
denna formel kan förenklas genom att multiplicera den med (1+r)/(1+r), vilket är att multiplicera den med 1. Detta avbryter många av dessa genom hela formeln, vilket lämnar
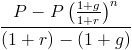
i nämnaren, (1+r) – (1+g) kommer att returnera r-g. vid denna punkt kan P och r-g räknas ut, vilket leder till nuvärdet av en växande livränta formel visas högst upp på sidan.
återgå till toppen
- formler relaterade till PV av en växande livränta
- PV av växande evighet
- växande livränta-betalning (PV)
- FV av växande livränta