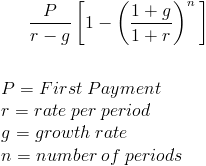
Der Barwert einer wachsenden Rente Formel berechnet den heutigen Wert einer Reihe von zukünftigen periodischen Zahlungen, die mit einer proportionalen Rate wachsen. Eine wachsende Rente kann manchmal als steigende Rente bezeichnet werden. Ein einfaches Beispiel für eine wachsende Rente wäre eine Person, die im ersten Jahr 100 US-Dollar erhält und die aufeinanderfolgenden Zahlungen für insgesamt drei Jahre um 10% pro Jahr steigen. Dies wäre eine Quittung von $ 100, $ 110 und $ 121.Der Barwert einer wachsenden Rentenformel beruht auf dem Konzept des Zeitwerts des Geldes. Die Prämisse dieses Konzepts ist, dass eine bestimmte Menge Geld heute mehr wert ist als zu einem zukünftigen Zeitpunkt.Wie bei allen Finanzformeln, die einen Zinssatz beinhalten, ist es wichtig, den Zinssatz pro Periode mit der Anzahl der Perioden im Barwert einer wachsenden Rentenformel zu korrelieren. Wenn die Zahlungen monatlich sind, dann müsste die Rate die monatliche Rate sein.
Wie wird der Barwert einer wachsenden Rente abgeleitet?
Der Barwert einer wachsenden Rente ist die Summe der zukünftigen Cashflows. Bei einer wachsenden Rente steigt jeder Cashflow mit einer bestimmten Rate. Die Formel für den Barwert einer wachsenden Rente kann geschrieben werden als
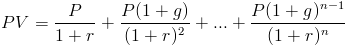
Diese Formel ist die allgemeine Formel zur Summierung der diskontierten zukünftigen Cashflows zusammen mit der Verwendung von 1 + g, um zu berücksichtigen, dass jeder zukünftige Cashflow mit einer bestimmten Rate zunimmt.
Dieser gegenwärtige Wert einer wachsenden Rentenformel kann dann umgeschrieben werden als
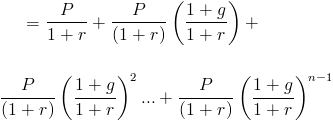
Dies würde als geometrische Reihe betrachtet, wobei (1 + g) /(1+r) das gemeinsame Verhältnis ist. Unter Verwendung der geometrischen Reihenformel wird der Barwert einer wachsenden Annuität angezeigt als
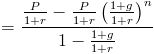
Diese Formel kann vereinfacht werden, indem sie mit (1 + r) / (1+r) multipliziert wird, dh mit 1 multipliziert wird. Dies hebt viele davon in der gesamten Formel auf, wodurch
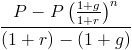
Im Nenner (1+ r) – (1+ g) wird r-g zurückgegeben. An dieser Stelle können P und r-g herausgerechnet werden, was zum Barwert einer wachsenden Annuitätsformel führt, die oben auf der Seite angezeigt wird.
Zurück zum Anfang
- Formeln im Zusammenhang mit PV einer wachsenden Annuität
- PV der Annuität
- PV der wachsenden Perpetuität
- Wachsende Annuität – Zahlung (PV)
- FV der wachsenden Annuität