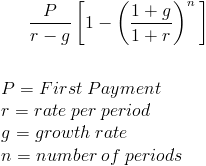
a növekvő járadék-képlet jelenlegi értéke kiszámítja a jövőbeli időszakos kifizetések sorozatának jelenlegi napi értékét, amely arányos ütemben növekszik. A növekvő járadékot néha növekvő járadéknak lehet nevezni. A növekvő járadék egyszerű példája az az egyén, aki az első évben 100 dollárt kap, az egymást követő kifizetések pedig évente 10% – kal növekednek, összesen három évig. Ez 100 dollár, 110 dollár, illetve 121 Dollár átvételi elismervény lenne.

a növekvő járadék formula jelenlegi értéke a pénz időértékének fogalmára támaszkodik. Ennek a koncepciónak az A előfeltétele, hogy egy adott pénzmennyiség ma többet ér, mint egy későbbi időpontban.

mint minden olyan pénzügyi képlet, amely egy kamatlábat tartalmaz, fontos, hogy az időszakonkénti kamatlábat korreláljuk a növekvő életjáradék-képlet jelenértékében szereplő időszakok számával. Ha a kifizetések havonta, akkor az arány lenne szükség, hogy a havi ráta.

hogyan származik a növekvő járadék jelenértéke?

a növekvő járadék jelenértéke a jövőbeli cash flow-k összege. A növekvő járadék esetében minden pénzforgalom egy bizonyos sebességgel növekszik. A képlet a jelen értéke egyre járadék lehet írni, mint

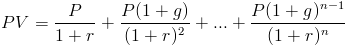
Ez a képlet az általános képlete összefoglalva a diszkontált jövőbeli cash flow-k együtt használva, 1 + g tényező, hogy minden jövőbeni cash flow növeli a konkrét mértéket.

Ez az ajándék értéke növekvő törlesztési forma lehet írni, mint a

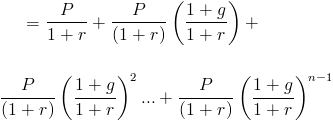
Ez tekinthető egy mértani sorozat, ahol (1+g)/(1+r) a közös arány. A geometriai sorozat képlet segítségével a növekvő életjáradék jelenértéke

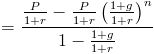
p > p > p > p > p > p > p > p + 1 + R) szorzatával egyszerűsíthető, amely 1-gyel szorozza meg. Ez törli ki sok ilyen az egész képlet, amely elhagyja

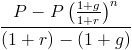
a nevező, (1 + r)- (1 + g) visszatér r-g. ezen a ponton, P és r-g lehet faktorált ki, ami oda vezet, hogy a jelenlegi értéke a növekvő járadék képlet látható az oldal tetején.

Vissza a lap Tetejére

• Képletek kapcsolatos PV Növekvő Járadék
• PV Járadék
• PV Növekvő Aránya
• Növekvő Járadék Kifizetés (PV)
• FV Növekvő Járadék