Pages Connexes
Plus de Leçons Sur les Ensembles
Intersection de Deux Ensembles
Intersection de Trois Ensembles

Les diagrammes suivants montrent les opérations des ensembles et les Diagrammes de Venn pour le Complément d’un Ensemble, les Ensembles Disjoints, les Sous-Ensembles, l’Intersection et l’Union des Ensembles. Faites défiler la page pour plus d’exemples et de solutions.

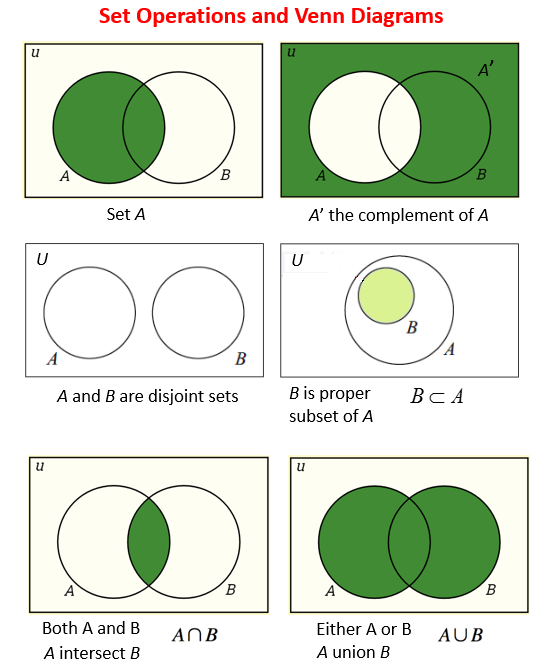
L’ensemble de tous les éléments considérés s’appelle l’Ensemble universel (U) et est représenté par un angle d’angle.

• Le complément de A, A’, est l’ensemble des éléments de U mais pas de A. A’ = {x/x ∈ U et x ∉ A}
• Les ensembles A et B sont des ensembles disjoints s’ils ne partagent aucun élément commun.
• B est un sous-ensemble propre de A. Cela signifie que B est un sous-ensemble de A, mais B ≠A.
• L’intersection de A et B est l’ensemble des éléments de l’ensemble A et de l’ensemble B. A BB = {x|x ∈ A et x ∈ B}
• L’union de A et B est l’ensemble des éléments de l’ensemble A ou de l’ensemble B. A BB = {x| x ∈ A ou x ∈ B}
• A == ∅
• A ==A

• Show Video Lesson

Définir Les Opérations Et Les Diagrammes De Venn

Exemple :
1. Créez un diagramme de Venn pour montrer la relation entre les ensembles.
U est l’ensemble des nombres entiers de 1 à 15.
A est l’ensemble des multiples de 3.
B est l’ensemble des nombres premiers.
C est l’ensemble des nombres impairs.

2. Étant donné le diagramme de Venn suivant, déterminez chacun des ensembles suivants.
a)A BB
b) A BB
c) (A BB) ‘
d) A’ ∩B
e) A BB’

• Montrer la leçon vidéo

Exemple:
Étant donné que l’ensemble P est l’ensemble des nombres pairs entre 15 et 25. Dessinez et étiquetez un diagramme de Venn pourprésenter l’ensemble P et indiquer tous les éléments de l’ensemble P dans le diagramme de Venn.

Solution:
Liste les éléments de P.
P = {16, 18, 20, 22, 24} ← ‘ entre ’ ne comprend pas 15 et 25
Dessinez un cercle ou un ovale. Étiquetez-le P. Mettez les éléments dans P.

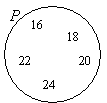
Exemple:
Dessinez et étiquetez un diagramme de Venn pour représenter l’ensemble
R={Lundi, mardi, mercredi}.

Solution:
Dessinez un cercle ou un ovale. Étiquetez-le R. Mettez les éléments dans R.

Exemple:
Étant donné l’ensemble Q= {x:2x-3 < 11, x est un entier positif}. Dessinez et étiquetez un diagramme de Venn pourprésenter l’ensemble Q.

Solution:
Puisqu’une équation est donnée, nous devons d’abord résoudre pour x.r–2x-3 <11 ⇒ 2x < 14 ⇒ x <7

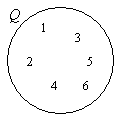
Donc, Q = {1, 2, 3, 4, 5, 6}
Dessinez un cercle ou un ovale. Étiquetez-le Q.
Mettez les éléments dans Q.

Vidéos de diagramme de Venn

Qu’est-ce qu’un diagramme de Venn et Que signifient Intersection et Union?

• Show Video Lesson

Diagramme de Venn – Deux sous-ensembles

Découvrez les diagrammes de Venn avec deux sous-ensembles.

• Afficher la leçon vidéo

Diagramme de Venn – Deux sous-ensembles utilisant des régions

Découvrez les diagrammes de Venn avec deux sous-ensembles utilisant des régions.

• Voir la leçon vidéo

Diagrammes de Venn avec trois sous-ensembles

Découvrez les diagrammes de Venn avec trois sous-ensembles.

• Afficher la leçon vidéo

Essayez la calculatrice Mathway gratuite et le résolveur de problèmes ci-dessous pour pratiquer divers sujets mathématiques. Essayez les exemples donnés, ou tapez votre propre problème et vérifiez votre réponse avec les explications étape par étape.