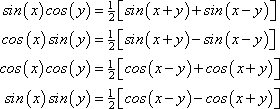Purplemath
En mathématiques, une « identité » est une équation qui est toujours vraie. Ceux-ci peuvent être « trivialement » vrais, comme « x = x » ou utilement vrais, comme « a2 + b2 = c2 » du théorème de Pythagore pour les triangles rectangles. Il existe de nombreuses identités trigonométriques, mais les suivantes sont celles que vous êtes le plus susceptible de voir et d’utiliser.
Basic & Pythagorean, Angle-Sum & -Difference, Double-Angle, Half-Angle, Sum, Product
Content Continues Below
MathHelp.com
Need a custom math course?
K12 | College | Test Prep

Identités de base et pythagoricienne
Affilié
Remarquez comment un « co- (quelque chose) » le rapport trigonométrique est toujours l’inverse d’un rapport « non-co ». Vous pouvez utiliser ce fait pour vous aider à garder droit que la cosécante va avec le sinus et la sécante va avec le cosinus.
Les identités suivantes (en particulier la première des trois ci-dessous) sont appelées identités « pythagoriciennes ».
sin2(t) + cos2(t) = 1
tan2(t) + 1=sec2(t)
1 +cot2(t) = csc2(t)
Publicité
Notez que les trois identités impliquent avant tout la quadrature et le nombre 1. Vous pouvez voir clairement la relation Pythagoricienne-Thereom si vous considérez le cercle unitaire, où l’angle est t, le côté « opposé » est sin(t) = y, le côté « adjacent » est cos(t) = x et l’hypoténuse est 1.
Nous avons des identités supplémentaires liées à l’état fonctionnel des rapports trigonométriques :
sin(–t)=–sin(t)
cos(–t) =cos(t)
tan(–t)=–tan(t)
Notez en particulier que le sinus et la tangente sont des fonctions impaires, symétriques par rapport à l’origine, tandis que le cosinus est une fonction paire, symétrique par rapport au y – axe. Le fait que vous puissiez prendre le signe « moins » de l’argument à l’extérieur (pour le sinus et la tangente) ou l’éliminer entièrement (pour le cosinus) peut être utile lorsque vous travaillez avec des expressions compliquées.
Identités de somme et de différence d’angle
sin(α + β)= sin(α) cos(β) + cos(α) sin(β)
sin(α-β) = sin(α) cos(β)-cos(α)sin(β)
cos(α + β) = cos(α) cos(β)–sin(α)sin(β)
cos(α–β) = cos(α) cos(β) + sin(α) sin(β)
À propos, dans les identités ci–dessus, les angles sont désignés par des lettres grecques. La lettre de type a, « α », est appelée « alpha », qui se prononce « AL-fuh ». La lettre de type b, « β », est appelée « bêta », qui se prononce « BAY-tuh ».
Le Contenu Continue Ci-Dessous
Identités À double angle
sin(2x) = 2 sin(x) cos(x)
cos(2x) = cos2(x) – sin2(x) = 1 – 2 sin2(x) = 2 cos2(x) – 1
Identifications d’angle
Les identités ci-dessus peuvent être réaffirmées en quadrant chaque côté et en doublant toutes les mesures d’angle. Les résultats sont les suivants:
Affiliate

Sum Identities
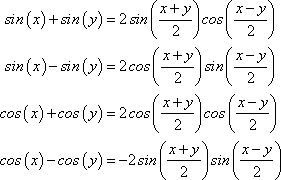
Product Identities
Affilié
Vous utiliserez toutes ces identités, ou presque, pour prouver d’autres identités trigonométriques et pour résoudre des équations trigonométriques. Cependant, si vous continuez à étudier le calcul, portez une attention particulière aux identités de demi-angle sinus et cosinus reformulées, car vous les utiliserez beaucoup dans le calcul intégral.
URL: https://www.purplemath.com/modules/idents.htm