Cette section couvre:

• Introduction aux Fonctions Par Morceaux
• Évaluation des Fonctions Par Morceaux
• Représentation Graphique de Fonctions Par Morceaux
• Comment Savoir si une Fonction Par Morceaux est Continue ou Non Continue
• Obtention d’équations à partir de Graphiques de Fonctions Par Morceaux
• Valeur Absolue en tant que Fonction Par Morceaux
• Transformations de Fonctions Par Morceaux
• Problèmes de Mots de Fonctions Par Morceaux
• Plus de pratique

Les fonctions par morceaux (ou les fonctions par morceaux) sont exactement ce qu’elles sont nommées: morceaux de différentes fonctions (sous-fonctions) le tout sur un graphique. La façon la plus simple d’y penser est de dessiner plus d’une fonction sur un graphique et d’effacer des parties des fonctions là où elles ne sont pas censées être (le long des \(x\)); elles sont définies différemment pour différents intervalles de \(x\). \(y\) est défini différemment pour différentes valeurs de \(x\); nous utilisons le \(x\) pour rechercher dans quel intervalle il se trouve, afin que nous puissions savoir ce que le \(y\) est censé être.

Notez qu’il existe un exemple d’inverse d’une fonction par morceaux ici dans la section Inverses of Functions.

Here’s an example and graph:

Piecewise Function

Graph

\(\displaystyle f\left( x \right)=\left\{ \begin{align}2x+8\,\,\,\,\,&\text{ if }x\le -2\\{{x}^{2}}\,\,\,\,\,\,\,\text{ }\,&\text{ if }x>-2\end{align} \right.\) (Il existe d’autres façons d’afficher cela, telles que l’utilisation d’un « for” au lieu d’un « if” et l’utilisation de virgules ou de points-virgules au lieu du « if”.) Domaine: \(\mathbb{R}, \,\,\ text{or}\,\,\left({-\infty, \infty}\right)\) Gamme: \(\mathbb{R}, \,\,\, \text {or}\,\,\left({-\infty,\infty}\right)\)

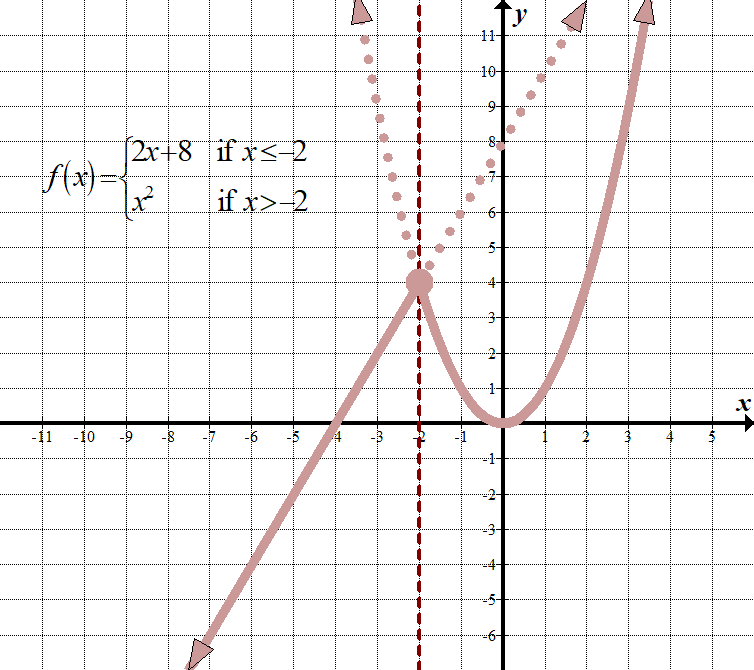Cela signifie que pour chaque \(x\) inférieur ou égal à -2, nous devons représenter graphiquement la ligne \(2x + 8\), comme si c’était la seule fonction du graphique. Pour chaque valeur \(x\) supérieure à -2, nous devons représenter graphiquement \({{x}^{2}}\), comme si c’était la seule fonction du graphique. Ensuite, nous devons « nous débarrasser » des pièces dont nous n’avons pas besoin. N’oubliez pas que nous utilisons toujours l’origine comme point de référence pour les deux graphiques!

Voyez comment la ligne verticale \(x=-2\) agit comme une ligne de « limite » entre les deux graphiques?

Notez que le point \((-2,4)\) a un cercle fermé dessus. Techniquement, il ne devrait appartenir qu’à la fonction \(2x + 8\), puisque cette fonction a le signe inférieur ou égal, mais comme le point se trouve également sur le graphe \({{x}^{2}}\), nous pouvons simplement utiliser un cercle fermé comme s’il apparaissait sur les deux fonctions. Tu vois, pas si mal, non?

Évaluation des fonctions par morceaux

Parfois, on vous donne des fonctions par morceaux et on vous demande de les évaluer; en d’autres termes, trouvez les valeurs \(y\) lorsque vous recevez une valeur \(x\). Faisons cela pour \(x =-6\) et \(x = 4\) (sans utiliser le graphique). Voici à nouveau la fonction :

\(\displaystyle f\left(x\right) =\left\{\begin{align} 2x+8\,\,\,\,\,& \text {if} x\le -2\\{{x}^{2}}\,\,\,\,\,\,\,\ text {}\, &\text {if} x > -2\end {align}\right.\)

Nous voulons d’abord regarder les conditions à droite, pour voir où se trouve notre \(x\). Lorsque \(x = -6\), nous savons qu’il est inférieur à -2, nous connectons donc notre \(x\) à \(2x + 8\) uniquement. \(f(x)\) ou \(y\) est \((2)(-6)+8=-4\). Nous ne nous soucions même pas du \(\boldsymbol{{x}^{2}}\)! C’est aussi simple que ça. Vous pouvez également voir que nous l’avons fait correctement en utilisant le graphique ci-dessus.

Essayez maintenant \(x= 4\). Nous regardons d’abord à droite, et voyons que notre \(x\) est supérieur à -2, nous le branchons donc dans le \({{x}^{2}}\). (Nous pouvons simplement ignorer le \(2x + 8\) cette fois.) \(f(x)\) ou \(y\) est \({{4}^{2}}=16\).

Représentation graphique de fonctions par morceaux

Il vous sera probablement demandé de représenter graphique de fonctions par morceaux. Parfois, les graphiques contiennent des fonctions non continues ou discontinues, ce qui signifie que vous devez prendre votre crayon au milieu du graphique lorsque vous le dessinez (comme un saut!). Les fonctions continues signifient que vous n’avez jamais à prendre votre crayon si vous deviez les dessiner de gauche à droite.

Et rappelez-vous que les graphiques ne sont des fonctions vraies que s’ils réussissent le test de la ligne verticale.

Dessinons ces fonctions par morceaux et déterminons si elles sont continues ou non continues. Notez comment nous dessinons chaque fonction comme si c’était la seule, puis « effaçons” les parties qui ne sont pas nécessaires. Nous obtiendrons également le Domaine et la plage comme nous l’avons fait ici dans la section des fonctions algébriques.

Piecewise Function	Graph
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-2x+8\,\,\,\,\,\,\text{if }x\le 4\\\frac{1}{2}x-2\,\,\,\,\,\,\,\,\,\text{if }x>4\end{array} \right.\) Continuous Domain: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) Range: \(\left( {0,\infty } \right)\)
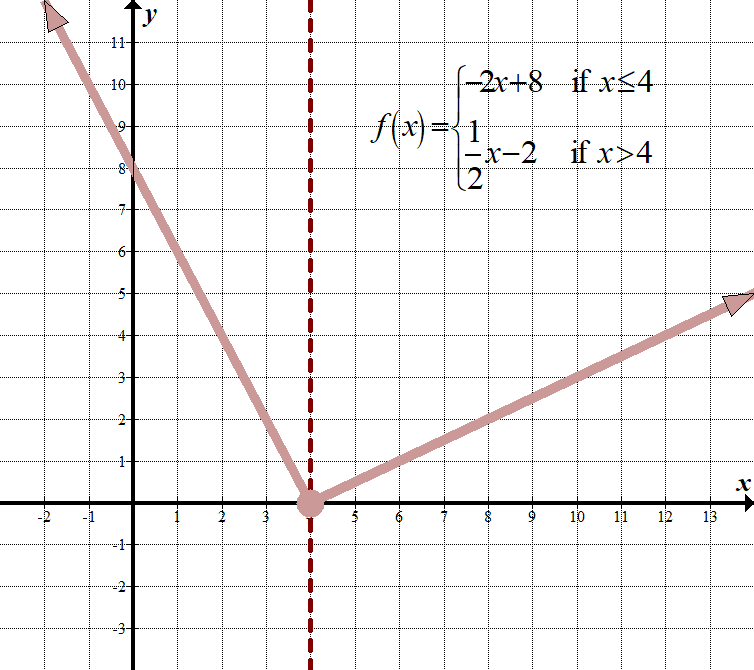\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\,\text{if }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1}\le x<4\\x-5\,\,\,\,\,\,\,\,\,\text{if }x\ge 4\end{array} \right.\) Non-Continuous Domain: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) Range: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\)

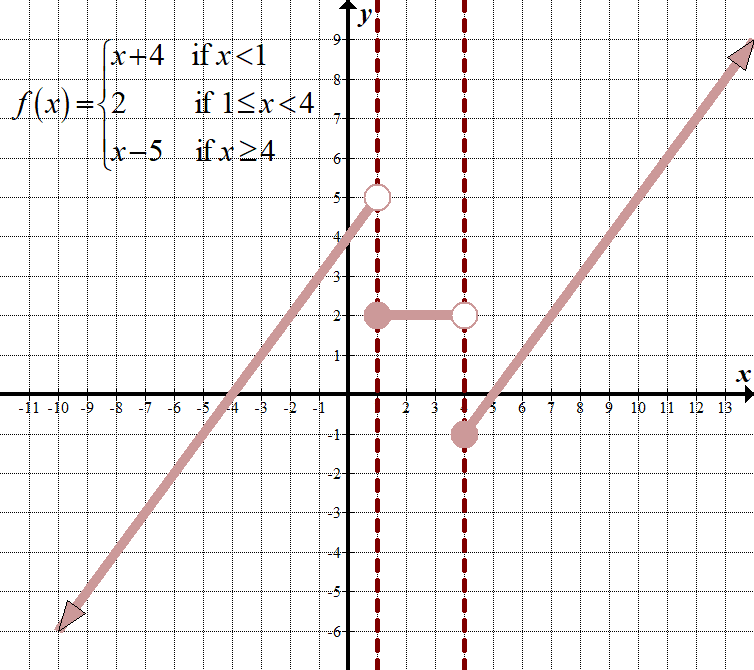We can actually put piecewise functions in the graphing calculator:

Piecewise Function Screens

Steps and Notes

Enter the piecewise function on three lines: Voici le graphique:

Pour mettre la fonction par morceaux \(\displaystyle f\left(x\right) = \left\{\begin{array } {l } x+4\,\,\,\,\,\,\,\,\,\ texte {if} x <1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ texte {if 1}\le x < 4\\-5+x\,\,\,\,\,\ texte {if} x\ge 4\ end {array}\ right.\) dans la calculatrice, vous pouvez entrer la fonction sur trois lignes en divisant la fonction dans chaque intervalle par une « inégalité de test » de cet intervalle (et regardez les parenthèses!). La raison pour laquelle nous divisons par les intervalles ou les inégalités est que la calculatrice renverra un 1 si l’inégalité (telle que \(x < 1\)) est vraie; par exemple, \((x + 4)\) finira juste par \((x + 4)/(1)\) lorsque \(x < 1\). Lorsque \(x\ge 1 \), nous divisons par 0, donc rien ne sera dessiné. Voici ce que nous pouvons mettre dans la calculatrice: \(\displaystyle\begin{array}{l}{{Y}_{1}} = \left({x+4}\right)/\left({x<1}\right)\\{{Y}_{2}} = \left(2\right) /\left({x\ge 1\text { et }x< 4}\right)\\{{Y}_{3}} = \left({-5+ x}\right)/\left({x\ge 4}\right)\end{array}\) (Notez que vous pouvez également saisir cela sur une ligne en multipliant les conditions au lieu de les diviser, et en utilisant des signes plus entre chacune des trois fonctions / intervalles: \(\displaystyle {{Y}_{1}} = \left({x+ 4}\right)\left({x <1}\right)+\left(2\right)\left({x\ge 1\text { and} x <4}\right)+\left({-5+x}\right) \left({x\ge 4}\ à droite)\).) Voici les frappes pour utiliser trois lignes. Notez que vous utilisez 2nd MATH (TEST) pour accéder à l’écran qui a le \(\le\), \(\ge\), et ainsi de suite. Par exemple, 2nd MATH 6 vous obtient \(\le\). Utilisez le 2ème TEST MATHÉMATIQUE, droit à la LOGIQUE, puis 1, pour le « et” dans \({{Y}_{2}}\).

Comment savoir si la fonction par morceaux est Continue ou Non continue

Pour savoir si un graphe par morceaux est continu ou non continu, vous pouvez regarder les points limites et voir si le point \(y\) est le même à chacun d’eux. (Si les \(y\) étaient différents, il y aurait un « saut » dans le graphique!)

Essayons ceci pour les fonctions que nous avons utilisées ci-dessus:

Piecewise Function	Check Boundary Points
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-2x+8\,\,\,\,\,\,\,\text{if }x\le 4\\\frac{1}{2}x-2\,\,\,\,\,\,\,\,\,\,\text{if }x>4\end{array} \right.\)	Let’s check \(x=4\) in both parts of the function, since 4 is the « boundary point”: \(\begin {array}{l}-2(4)+8=0\\\,\,\,\ frac{1}{2}(4)-2=0\ end{array}\) Depuis \(0 = 0\), cette fonction par morceaux est continue.
\(\displaystyle f\left(x\right) = \left\{\begin{array}{l} x+4\,\,\,\,\,\,\,\,\,\,\,\,\,\ texte {if} x <1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ texte {if 1}\le x < 4\\-5+x\,\,\,\,\,\,\,\,\,\ texte {if} x\ge 4\ end {array}\ right.\)	Vérifions les deux premières parties de la fonction. Remarque dans la deuxième partie, \(y\) vaut toujours 2: \(\begin {array}{l}1+4=5\\\,\,\,\,\,\,\,\,\,2=2\ end{array}\) Depuis \(5\ne 2\), nous pouvons nous arrêter ici et noter que cette fonction par morceaux est non continue. Si les \(y\) étaient égaux, il faudrait aller un pour vérifier le point limite suivant à \(x = 4\).

Obtention d’équations à partir de graphiques de fonctions par morceaux

On peut vous demander d’écrire une fonction par morceaux, étant donné un graphique. Maintenant que nous savons ce que sont les fonctions par morceaux, ce n’est pas si mal!

Pour voir comment obtenir des équations à partir de graphes linéaires, voir Obtention des équations d’une Droite, et à partir de la quadratique, voir Recherche d’une équation quadratique à partir de Points ou d’un graphique.

Voici les graphiques, avec des explications sur la façon de dériver leurs équations par morceaux:

Piecewise Function Graph	Procedure to get Function
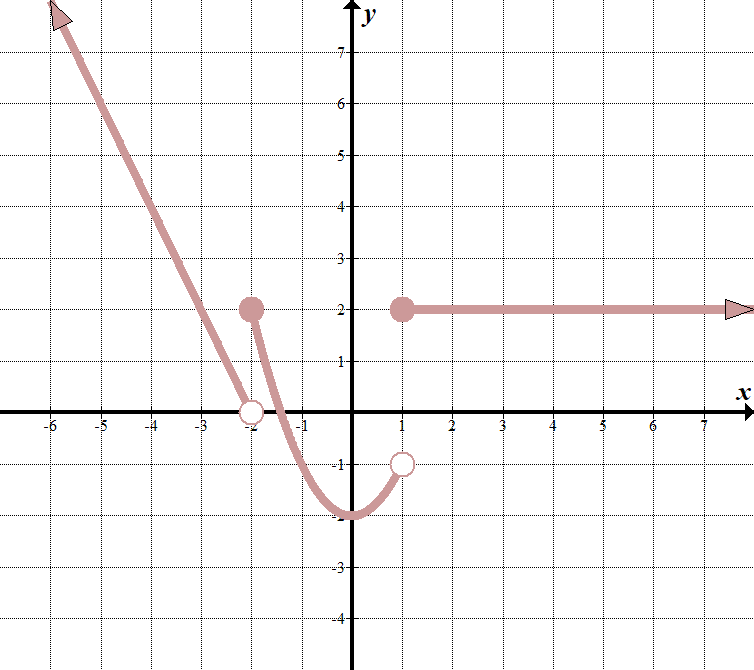	We see that our « boundary lines” are at \(x=-2\) and \(x=1\). We know that our function will look something like this (notice open and closed endpoints): \(\displaystyle f\left(x\right) =\left\{\begin{array}{l}\text{ }……\,\,\,\,\,\,\,\,\ texte {if} x < -2\\\ texte{ }……\,\,\,\,\,\,\,\,\ text {if}-\text {2}\le x < 1\\\text{ }……\,\,\,\,\,\,\,\,\ texte {if} x\ge 1\end {array}\ right.\) Nous pouvons choisir deux points \((-2,0)\) et \((-3,2)\) sur la ligne la plus à gauche pour obtenir l’équation \(y =-2x-4\). La fonction du milieu est \(y = {{x}^{2}}-2\), et la fonction la plus à droite est juste la ligne horizontale \ (y = 2\). Ainsi, la fonction par morceaux est: \(\displaystyle f\left(x\right) =\left\{\begin{array}{l}-2x-4\,\,\,\,\,\,\,\ texte {if}x < -2 \\\ texte {} {{x}^{2}}-2\,\,\,\,\,\,\,\,\,\,\ text {if}-\text {2}\le x < 1\\\text{ 2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ texte {if} x\ge 1\end {array}\ right.\)
	Nous voyons quenotre ”ligne de limite » est à \(x = 5\). Puisque les lignes se rencontrent à \((5,4)\), peu importe où nous mettons le signe \(\le\) ou \(\ge\); nous ne pouvons tout simplement pas le mettre aux deux endroits, sinon ce ne serait pas une fonction. Nous avons jusqu’à présent: \(\displaystyle f\left(x\right) =\left\{\begin{array}{l}\text{ }……\,\,\,\,\,\,\,\,\,\ texte {if}x < 5\\\ texte{ }……\,\,\,\,\,\,\,\,\,\ texte {if} x\ge 5\ end {array}\ right.\) Encore une fois, nous devons regarder chaque ligne séparément pour déterminer leurs équations. Nous pouvons soit prendre 2 points de chaque ligne pour les obtenir, soit dériver des pentes et des interceptions \(y\); la fonction par morceaux est: \(\displaystyle f\left(x\right)=\left\{\begin{array}{l}\frac{6}{5}x-2\,\,\,\,\,\,\,\ texte {if}x < 5\\\frac {2}{5}x+2\,\,\,\,\,\,\,\ texte {if} x\ge 5\ end {array}\ right.\)

Valeur absolue comme fonction par morceaux

Nous pouvons écrire des fonctions de valeur absolue comme fonctions par morceaux – c’est vraiment cool! Vous voudrez peut-être passer en revue La Résolution d’Équations et d’inégalités de valeur Absolue avant de continuer sur ce sujet.

Disons que nous avons la fonction \(f\left(x\right) = \left/x\right|\). D’après ce que nous avons appris plus tôt, nous savons que lorsque \(x\) est positif, puisque nous prenons la valeur absolue, ce sera toujours juste \(x\). Mais lorsque \(x\) est négatif, lorsque nous prenons la valeur absolue, nous devons prendre l’inverse (la nier), car la valeur absolue doit être positive. Avoir du sens ? Ainsi, par exemple, si nous avions \(/5/\), nous prenons simplement ce qui est à l’intérieur du signe absolu, car c’est positif. Mais pour \(|-5|\), nous devons prendre l’opposé (négatif) de ce qui se trouve à l’intérieur de la valeur absolue pour en faire \(\displaystyle 5\,\,\,(-\,-5=5)\).

Cela signifie que nous pouvons écrire cette fonction de valeur absolue comme une fonction par morceaux. Notez que nous pouvons obtenir le « point tournant” ou le « point limite” en définissant tout ce qui se trouve à l’intérieur de la valeur absolue à 0. Ensuite, nous utiliserons la fonction d’origine ou annulerons la fonction, en fonction du signe de la fonction (sans la valeur absolue) dans cet intervalle.

Par exemple, nous pouvons écrire \(\displaystyle\left/x\right/\text {} = \left\{\begin{array}{l}x\,\,\,\,\,\,\,\,\,\ texte {if} x\ge 0\\-x\,\,\,\,\,\ texte {if} x < 0\end {array}\right.\). Notez également que, si la fonction est continue (il n’y a pas de « saut”) au point limite, peu importe où nous mettons les signes « inférieur ou égal à” (ou « supérieur ou égal à”), tant que nous ne les répétons pas! Nous ne pouvons pas les répéter car, théoriquement, nous ne pouvons pas avoir deux valeurs de \(y\) pour le même \(x\), sinon nous n’aurions pas de fonction.

Here are more examples, with explanations. (You might want to review Quadratic Inequalities for the second example below):

Absolute Value Function	Method to get Piecewise Function
\(g\left( x \right)=\left| {2x+3} \right|\)	Let’s first find the « boundary line”. Pour ce faire, nous définissons ce qui se trouve à l’intérieur de la valeur absolue sur 0, puis résolvons \(\boldsymbol{x}\). Lorsque \(2x + 3\ge 0\), nous obtenons \(\displaystyle x\ge-\frac{3}{2}\) (en fait, nous pouvons garder le \(\ge\) lorsque nous résolvons). Lorsque \(2x + 3\) est positif, nous le prenons simplement « tel quel », mais si c’est négatif, nous devons tout nier. Par conséquent, la fonction par morceaux est: \(\displaystyle\left/{2x+3}\right|=\left\{\begin{array}{l} 2x+3\,\,\,\,\,\,\,\,\,\ texte {if} x\ge-\frac {3}{2} \ texte {}\\-2x-3\,\,\,\,\,\ texte {if}x < -\frac{3}{2}\ end{array}\right.\) Essayez–le – ça marche!
\(f\left(x\right)=\left|{{{x}^{2}} -4}\right/\)	Trouvons d’abord la « ligne(s) de limite”; nous définissons ce qui se trouve à l’intérieur de la valeur absolue à 0. Lorsque \({{x}^{2}} -4\ge 0\), nous obtenons \(x\le -2\) ou \(x\ge 2\) (essayez quelques nombres!). Lorsque \({{x}^{2}} -4\) est positif, nous le prenons simplement « tel quel », mais s’il est négatif, nous devons le nier. La fonction par morceaux est: \(\displaystyle\left/{{{x}^{2}} -4}\right/=\left\{\begin{array}{l}{{x}^{2}}-4\,\,\,\,\,\ texte {if} x\le -2\\4 – {{x}^{2}}\,\,\,\,\,\ texte {if} -2 < x < 2\\{{x}^{2}}-4\,\,\,\,\,\ text {if} x\ge 2\text {}\end {array}\right.\) ou \(\displaystyle\left/{{{x}^{2}} -4} \right/= \left\{\begin{array}{l}{{x}^{2}}-4\,\,\,\,\,\,\ texte {if} x\le -2\texte {}\,\,\texte { ou} \,\,\texte {} x\ge 2\\4 – {{x}^{2}}\,\,\,\,\,\,\,\ text {if} -2 < x < 2\end {array}\right.\) Encore une fois (puisque la fonction est continue), peu importe où nous avons les \(\le\) et \(\ge\) (par opposition à \(<\) et \(>\)), tant que nous ne les répétons pas.
\(f\left(x\right) = 2x + \left |{x + 2}\right /\)	Celui-ci est un peu plus délicat, car nous avons un \(x\) à l’intérieur et à l’extérieur de la valeur absolue. Pour la « ligne de limite », nous n’utilisons que ce qui se trouve à l’intérieur de la valeur absolue. Lorsque \(x + 2\ge 0\), nous obtenons \(x\ge-2\). Mais pour la fonction par morceaux, nous devons utiliser la fonction entière, y compris la partie qui est en dehors de la valeur absolue. Ainsi, la fonction par morceaux est: \(\displaystyle 2x+\left/{x+2}\right|=\left\{\begin{array}{l} 2x+x+2\,\,\,\,\,\ texte {si} x\ge-2\\2x-x-2\,\,\,\,\,\ texte {if} x < -2\end {array}\right.\) Simplifions: \(\displaystyle 2x +\left/{x+2}\right|=\left\{\begin{array}{l}3x+2\,\,\,\,\,\,\,\ texte {si} x\ge -2\\x-2\,\,\,\,\,\,\,\,\,\,\ texte {if} x < -2\end {array}\right.\) Essayez des valeurs inférieures à et super alors -2; elles devraient fonctionner!
\(g\left(x\right)=\left |{{{x}^{2}}-4x-5}\right |\)	Celui-ci est mieux résolu avec un graphique de signes car nous avons un quadratique et nous devons savoir où la fonction est positive et négative . Tout d’abord, factorisez le quadratique à l’intérieur de la fonction de valeur absolue à \(\left({x-5}\right)\left({x+1}\right)\). Utilisez ensuite un tableau de signes pour voir où les facteurs sont positifs et négatifs, et rappelez-vous que lorsque les facteurs sont positifs, nous utilisons la fonction « telle quelle”, et lorsque les facteurs sont négatifs, nous annulons la fonction: \(\displaystyle\left/{{{x}^{2}} – 4x-5}\right|=\left\{\begin{array}{l}{{x}^{2}} – 4x-5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ texte {if} x\le -1\,\,\,\,\ texte {ou} \, \, \, \, x\ge 5 \\-\ gauche ({{{x}^{2}} – 4x-5} \ droite)\,\,\,\,\ text {if} -1 < x < 5\text{}\end {array}\right.\)
\(\displaystyle g\left(x\right) = \frac {{\left|{x+2}\right|}} {{x+2}}\)	C’est une fonction rationnelle, car il y a une variable dans le dénominateur. Lorsque \(x + 2\ge 0\), nous obtenons \(\displaystyle x\ge-2\). Lorsque \(x + 2\) est positif, nous le prenons simplement « tel quel », mais s’il est négatif, nous devons nier ce qui est dans la valeur absolue: \(\displaystyle\frac{{\left/{x + 2}\right|}} {{x +2}} = \left\{\begin{array}{l}\frac{{x +2}}{{x+2}}\,\,\,\,\,\,\,\,\,\ texte {if} x\ge-2\\\ frac {{-x-2}} {{x+2}}\,\,\,\,\,\,\ texte {if} x < -2\end {array}\right.\). Mais il faut être prudent, puisque \(x\ne 2\) (restriction de domaine: le dénominateur serait 0). Par conséquent, la fonction par morceaux est: \(\displaystyle\frac {{\left/{x+2}\right/}} {{x+2}} = \left\{\begin{array}{l}1\,\,\,\,\,\,\,\,\,\,\ texte {if} x >-2\\-1\,\,\,\,\,\,\ texte {if} x < -2\end {array}\right.\).

On peut également vous demander de prendre un graphique en valeur absolue et de l’écrire comme une fonction par morceaux:

Absolute Value Graph	Method to get Piecewise Function
	We see that our « boundary line” is at \(x=0\), so what’s inside the absolute value sign must be \(x\) or a factor of \(x\). (En effet, pour obtenir la ligne de limite avec une fonction de valeur absolue, nous définissons ce qui se trouve à l’intérieur de la valeur absolue sur 0, et résolvons pour \(x\)). Lorsque \(x > 0\), nous pouvons voir que l’équation de la droite est \(y = 2x-2\). Lorsque \(x < 0\), l’équation est \(y = 2x-2\). Nous pouvons écrire ceci comme une fonction par morceaux : \(\displaystyle f\left(x\right)=\left\{\begin{array}{l}2x-2\,\,\,\,\,\,\,\ text {if}x > 0\\-2x-2\,\,\,\text {if} x\le 0\end {array}\right.\) Nous pouvons également écrire ceci comme une fonction de valeur absolue transformée: \(y = 2\left/x\right|-2\) ou \(y= \left/{2x}\right|-2\) (puisque 2 est positif, il peut être à l’intérieur ou à l’extérieur du \(\left|{\,\,}\right|\)). (Cela a du sens car lorsque ce qui est à l’intérieur du \(\left|{\,\,}\right |\) est \(> 0\), nous utilisons la fonction régulière \(y = 2x-2\), et lorsque ce qui est à l’intérieur du est \(< 0\), nous annulons la partie valeur absolue pour le faire \(y =-\left({2x} \ droite) -2\)).
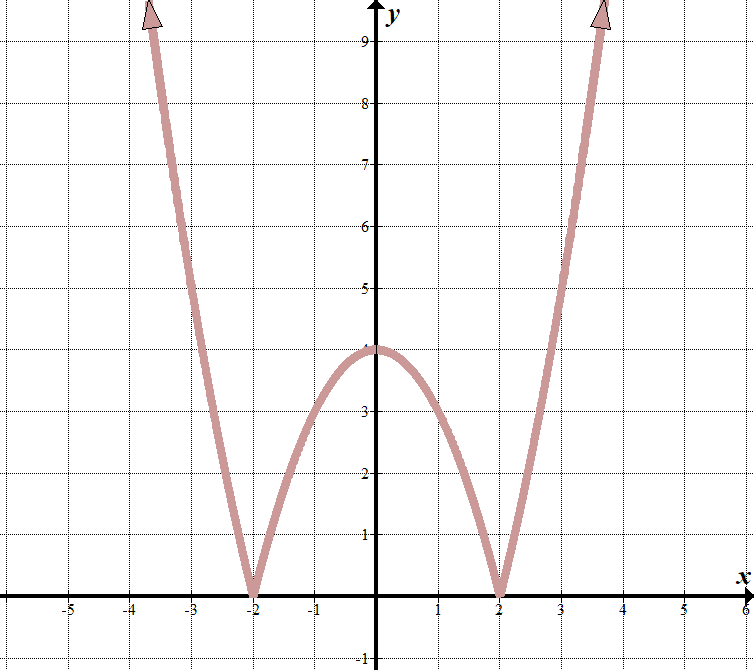	Nous voyons que nos « lignes de limite” sont à \(x = 2 \) et \(x =-2 \), donc ce qui est à l’intérieur du signe de valeur absolue doit avoir des facteurs de \ (x-2\) et \(x+2\). Lorsque \(x <-2\) ou \(x >2\), nous pouvons voir que le graphique ressemble à la partie normale du graphique \(y = {{x}^{2}}-4\). (J’ai compris cela en connaissant les facteurs et en prenant une bonne estimation!) Lorsque \(-2 < x <2\), l’équation est retournée ou annulée (retournée sur l’axe \(x\)). Nous pouvons écrire ceci comme une fonction par morceaux : \(\displaystyle f\left(x\right)=\left\{\begin{array}{l}{{x}^{2}}-4\,\,\,\,\,\,\,\,\,\ texte {if}x < -2\texte {or}x > 2\\-{{x}^{2}}\ texte{+ 4}\,\,\,\,\,\,\ texte {if} -2\le x\le 2\ end {array}\ right.\) Nous pouvons voir que cela a commencé une fonction quadratique transformée \(y= {{x}^{2}} -4\) avec une valeur absolue autour d’elle, puisque toutes les valeurs \(y\) sont positives: \(y = \left |{{{x}^{2}} -4} \right |\).
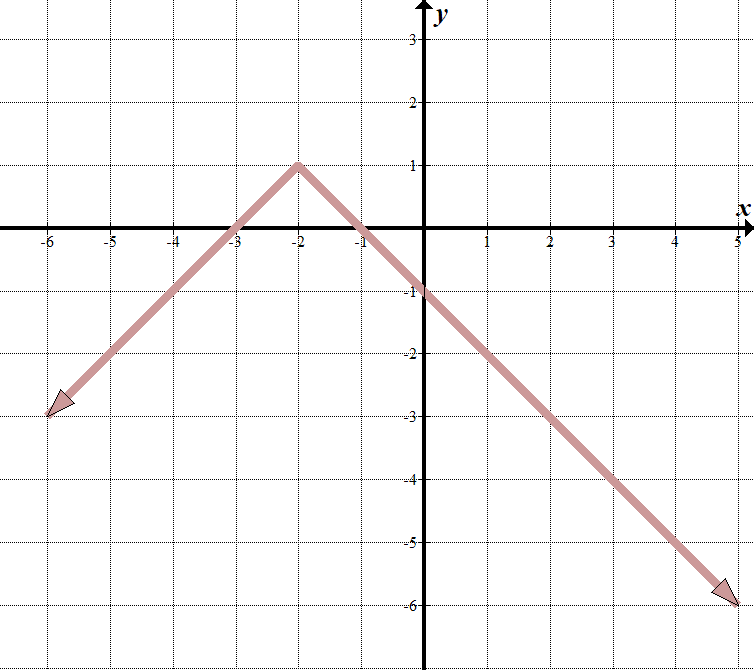	Nous voyons que notre ”ligne de limite » est à \(x =-2\), donc ce qui est à l’intérieur du signe de valeur absolue doit être \(x + 2\). Lorsque \(x >-2\), nous pouvons voir que l’équation de la droite est \(y =-x-1\). Lorsque \(x < -2\), la ligne est \(y = x +3\). Nous pouvons écrire ceci comme une fonction par morceaux : \(\displaystyle f\left(x\right)=\left\{\begin{array}{l}-x-1\,\,\,\,\,\,\ texte {if} x > -2\\x+3\,\,\,\,\,\,\,\,\,\,\ texte {if} x\le -2\ end {array}\ right.\) Il est probablement plus facile d’écrire ceci comme une fonction de valeur absolue transformée. Nous pouvons voir que la fonction de valeur absolue parente est retournée verticalement, se déplace vers la gauche 2 et vers le haut 1. Notre équation de valeur absolue est \(y = -\left /{x +2}\right|\,\,+\,\,1\). C’est la même chose que la fonction par morceaux ci-dessus. Essayez–le – ça marche!

Transformations de fonctions par morceaux

Faisons une transformation d’une fonction par morceaux. Nous avons appris à propos des Fonctions parentes et de leurs Transformations ici dans la section Graphiques et transformations parentes. Vous voudrez probablement d’abord lire cette section avant d’essayer une transformation par morceaux.

Transformons la fonction suivante par morceaux retournée autour de l’axe \(x\), étirée verticalement par un facteur de 2 unités, 1 unité vers la droite et 3 unités vers le haut.

Nous allons dessiner \(-2f\left(x-1\right) +3\), où:

\(\displaystyle f\left(x\right) =\left\{\begin{align}x+4\,\,\,\,\,\,\,\,&\text {if} x <&\text {if 1}\le x < 4\\x-5\,\,\,\,\,\,\,\,&\text {if} x\ge 4\end {align}\right.\)

Assurons-nous d’utiliser les points « limites » lorsque nous remplissons le graphique en t pour la transformation. Rappelez-vous que les transformations à l’intérieur des parenthèses sont faites au \(x\) (en faisant le calcul inverse), et à l’extérieur sont faites au \(y\). Pour créer un graphique en t, comme indiqué dans le tableau ci-dessous, nous pouvons utiliser des points clés, y compris deux points sur chacune des « lignes de démarcation”.

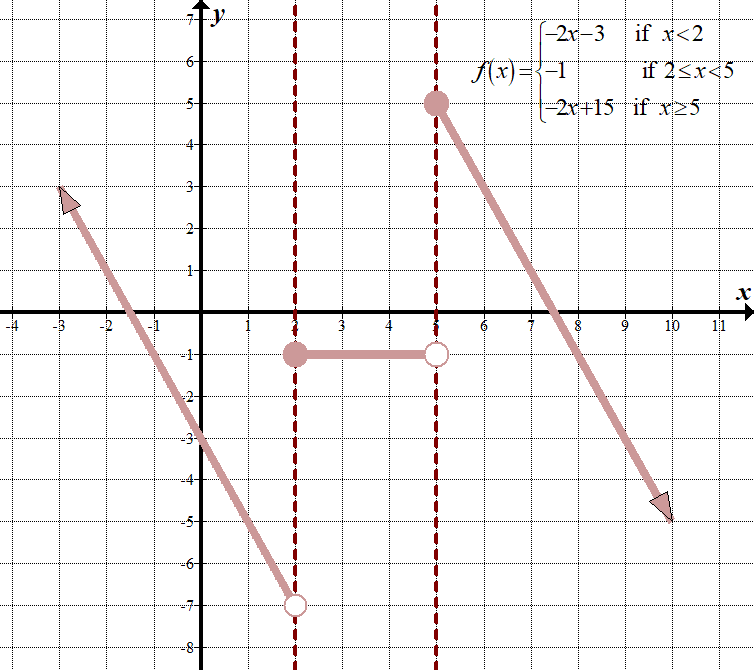
Notez que parce que cette transformation est compliquée, nous pouvons créer une nouvelle fonction par morceaux en transformant les 3 « pièces” et en transformant également les « \(x\)” où se trouvent les points limites (en ajoutant 1, ou en allant vers la droite 1), puisque nous faisons le calcul inverse pour les « \(x\)”. Pour obtenir les nouvelles fonctions dans chaque intervalle, nous pouvons simplement remplacer « \(x-1\) » par « \(x\) » dans l’équation d’origine, multiplier par -2, puis ajouter 3. Par exemple, \(\displaystyle-2f\left({x-1}\right) +3 =-2\left +3 = -2\left({x+3}\right) +3 =-2x-3\).

\(\displaystyle-2f\left({x-1}\right) +3=\left\{\begin{array}{l} -2\left({\left({x-1}\right) +4}\right) +3 = -2x-3,\,\,\,\,\ texte {if} x-1 < 1\,\,\,\ left({x <2}\ right)\\-2\left(2\right)+3=-1,\,\,\,\,\ text {if}\,\text {2}\le x < 5\\-2\left({\left({x-1}\right) -5}\right) +3 =- 2x+15,\,\,\,\,\ texte {if} x\ge 5\ end {array}\ right.\)

Voici les graphiques « avant » et « après », y compris le graphique en t:

Piecewise Parent Function	T-chart	Transformation of Function
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\text{if }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1 }\le x<4\\x-5\,\,\,\,\,\,\,\,\text{if }x\ge 4\end{array} \right.\)	x + 1 x y –2y+3 1 0 4 –5 2 1 5 –7 2 1 2 –1 5 4 2 –1 5 4 –1 5 8 7 2 –1	\(\displaystyle -2f\left( {x-1} \right)+3=\left\{ \begin{array}{l}-2x-3\,\,\,\,\,\,\,\,\,\text{if }x<2\\-1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 2}\le x<5\\-2x+15\,\,\,\,\,\,\text{if }x\ge 5\end{array} \right.\)

Piecewise Function Word Problems

Problem:

Votre toiletteur préféré se charge en fonction du poids de votre chien. Si votre chien a 15 livres et moins, le toiletteur facture 35 $. Si votre chien pèse entre 15 et 40 livres, elle facture 40 $. Si votre chien a plus de 40 livres, il facture 40 $, plus 2 additional supplémentaires pour chaque livre.

(a) Écrivez une fonction par morceaux qui décrit ce que charge votre toiletteur pour chiens.

(b) Graphise la fonction.

(c) Que facturerait le toiletteur si votre chien mignon pèse 60 livres?

Solution:

(a) Nous voyons que les ”points limites » sont 15 et 40, car ce sont les poids où les prix changent. Puisque nous avons deux points limites, nous aurons trois équations dans notre fonction par morceaux. Nous devons commencer à 0, car les chiens doivent peser plus de 0 livres:

\(\displaystyle f\left(x\right) =\left\{\begin{array}{l}\text{ }……\,\,\,\,\,\,\,\,\,\ text {if}0 < x\le 15\\\text{ }……\,\,\,\,\,\,\,\,\,\ texte {if}15 < x\le 40\\\text{ }……\,\,\,\,\,\,\,\,\,\ texte {if} x > 40\end {array}\right.\)

Nous recherchons les « réponses” (combien coûte le toilettage) aux « questions” (combien pèse le chien) pour les trois gammes de prix. Les deux premiers ne sont que des frais fixes (35$ et 40 respectively, respectivement). La dernière équation est un peu plus délicate; le toiletteur facture 40 $ plus 2 pound pour chaque livre de plus de 40 livres. Essayons les chiffres réels: si votre chien pèse 60 livres, il facturera 40 plus plus 2 fois \ (20 (60-40)\). Nous allons transformer cela en une équation: \(40 + 2(x–40) \), ce qui se simplifie en \(2x-40 \) (voir comment 2 est la pente?).

Toute la fonction par morceaux est:

\(\displaystyle f\left(x\right) =\left\{\begin{array}{l}\text{ }35\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ text {if}0 < x\le 15\\\text{ }40\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ texte {if}15 < x\le 40\\\text {}40 +2\left({x-40}\right)\,\,\,\,\,\,\ texte {if} x > 40\end {array}\right.\) ou \(\displaystyle f\left(x\right) = \left\{\begin{array}{l}\text{ }35\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ text {if}0 < x\le 15\\\text{ }40\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ texte {if}15 < x\le 40\\\text {}2x-40\,\,\,\,\,\,\,\ texte {if} x > 40\end {array}\right.\)

(b) Graphiquement: Notez que cette équation par morceaux est non continue. Notez également qu’un domaine raisonnable pour ce problème pourrait être \(\left({0,200} \right]\) (étant donné que les chiens ne pèsent pas plus de 200 livres!) et une plage raisonnable peut être \(\left\cup\left\).

(c)Si votre chien pèse 60 livres, nous pouvons soit utiliser le graphique, soit la fonction pour voir que vous devrez payer 80 $. Ouah! Cela coûte plus cher qu’une coupe de cheveux humaine (du moins mes coupes de cheveux)!

Problème:

Vous envisagez de vendre des t-shirts She Love Math comme collecte de fonds. La société de vente en gros de t-shirts vous facture 10 a la chemise pour les 75 premières chemises. Après les 75 premières chemises que vous achetez jusqu’à 150 chemises, la société baissera son prix à 7,50 per par chemise. Après avoir acheté 150 chemises, le prix diminuera à 5 per par chemise. Écrivez une fonction qui modèle cette situation.

Solution:

Nous voyons que les « points limites” sont 75 et 150, car il s’agit du nombre de t-shirts achetés là où les prix changent. Puisque nous avons deux points limites, nous aurons trois équations dans notre fonction par morceaux. Nous allons commencer par \(x\ge 1 \), car nous supposons qu’au moins une chemise est achetée. Remarque dans ce problème, le nombre de t-shirts achetés (\(x\)), ou le domaine, doit être un entier, mais cette restriction ne devrait pas affecter l’issue du problème.

\(\displaystyle f\left(x\right)=\left\{\begin{array}{l}\text{}……\text{if} 1\le x\le 75\\text{}……\text{if} 75 < x\le 150\\\ text {}……\text {if} x > 150\end {array}\right.\)

Nous recherchons les « réponses » (coût total des t-shirts) aux ”questions » (combien sont achetés) pour les trois gammes de prix.

Pour jusqu’à 75 chemises incluses, le prix est de 10 $, donc le prix total serait \(10x\). Pour plus de 75 chemises mais jusqu’à 100 chemises, le coût est de 7,50 $, mais les 75 premiers t-shirts coûteront toujours 10 per par chemise. La deuxième fonction comprend les 750 spent dépensés pour les 75 premières chemises (75 fois 10 $), et comprend également 7,50 times fois le nombre de chemises de plus de 75, ce qui serait \((x-75)\). Par exemple, si vous avez acheté 80 chemises, vous devrez dépenser \ (\times 10 \ fois 75 = \7 750\), plus \ (\7 7,50\ fois 5\,\) (80 – 75) pour les chemises après la 75e chemise.

De même, pour plus de 150 chemises, nous paierions toujours le prix de 10 $ à travers 75 chemises, le 77.50 prix pour 76 à 150 chemises (75 chemises de plus), puis 5 per par chemise pour le nombre de chemises achetées plus de 150. Nous paierons \(10(75)+7.50(75)+5( x-150)\) pour les chemises \(x\). Mettez en chiffres et essayez-le!

Toute la fonction par morceaux est:

\(\displaystyle f\left(x\right) =\left\{\begin{array}{l}\text{} 10x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ texte {if} 1\le x\le 75\\\ texte {} 7,5x\texte {} +\texte{ }187.5\,\,\,\,\,\ texte {if 7} 5 < x\le 150\\\text {} 5x+562.5\,\,\,\,\,\,\,\,\,\,\ texte {if} x > 150\end {array}\right.\) ou \(\displaystyle f\left(x\right) = \left\{\begin{array}{l}\text{} 10x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ texte {if} 1\le x\le 75\\\ texte {} 7,5x\texte {} +\texte{ }187.5\,\,\,\,\,\ texte {if 7} 5 < x\le 150\\\text {}5x+562.5\,\,\,\,\,\,\,\,\,\,\,\ texte {if} x > 150\end {array}\right.\)

Problème :

Un service de bus coûte 50 $ pour les 400 premiers milles, et chaque 300 milles supplémentaires (ou une fraction de ceux-ci) ajoute 10 miles au tarif.

Utilisez une fonction par morceaux pour représenter le tarif du bus en termes de distance en miles.

Solution:

C’est en fait un problème délicat, mais pensons d’abord au « point limite”, qui est 400. C’est assez simple lorsque le trajet dure moins de 400 miles; le coût est de 50 $.

Pour plus de 400 miles, nous devons soustraire les 400 premiers miles (mais n’oubliez pas d’inclure les 50 premiers $), diviser le nombre de miles restants par 300 miles (et arrondir, s’il y a un montant fractionnaire), et multiplier cela par 10 $.

La partie délicate est quand nous « arrondissons » pour une partie des 300 prochains miles. On peut utiliser une fonction ”plafond » (désignée par \(\left\lceil{}\right\rceil\)); cette fonction donne le plus petit entier supérieur ou égal à son entrée; par exemple, le plafond de 3,5 et 4 est 4.

Ainsi, c’est ce que nous avons:

\(\displaystyle f\left(x\right) =\left\{\begin{array}{l}\text{} 50\text{ }\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ text {if} 0\le x\le 400\\\text {} 50 + 10\times\left\lceil{\frac{{x-400}}{{300}}} \ droit \rceil\ texte{ }\,\,\,\,\,\,\ texte {if} x > 400\end {array}\right.\)

Essayons! Si nous avons un trajet de 1500 milles, le coût serait \(\displaystyle 50 + 10\times\left\lceil{\frac{{1500-400}}{{300}}} \ droit \rceil\text {} = 50 + 10\fois 4 = \990\).

Problème:

Quelle valeur de \(\boldsymbol{a}\) rendrait cette fonction continue par morceaux ?

\(\displaystyle f\left(x\right) =\left\{\begin{array}{l}3 {{x}^{2}}+4\,\,\,\,\,\ texte {if} x < -2\\5x +\boldsymbol {a}\,\,\,\,\,\,\,\,\ texte {if} x\ge -2\ end {array}\ right.\)

Solution:

Pour que la fonction par morceaux soit continue, au point limite (où la fonction change), les deux valeurs \(y\) doivent être les mêmes. Nous pouvons brancher -2 pour \(x\) dans les deux fonctions et nous assurer que les \(y\) sont les mêmes

\(\begin{align}3 {{x}^{2}} +4 &= 5x + a\\3 {{\left({-2}\right)}^{2}}+4&=5\left({-2}\right) + a\\12 +4 &=-10 +a\\a &=26\end{align}\)

Si \(a=26\), la fonction par morceaux est continu!

Apprenez ces règles, et pratiquez, pratiquez, pratiquez!

Plus de pratique: Utilisez le widget Mathway ci-dessous pour essayer d’écrire une fonction par morceaux. Cliquez sur Soumettre (la flèche bleue à droite du problème) et cliquez sur Écrire la Valeur Absolue par morceaux pour voir la réponse.

Vous pouvez également saisir votre propre problème, ou cliquer sur les trois points dans le coin supérieur droit et cliquer sur « Exemples” pour explorer par sujet.

Si vous cliquez sur Appuyez pour afficher les étapes, ou cliquez ici, vous pouvez vous inscrire à Mathway pour un essai gratuit, puis passer à un abonnement payant à tout moment (pour résoudre tout type de problème mathématique!).

Passez aux Matrices et Résolvez des Systèmes avec des Matrices – vous êtes prêt !