Une corrélation est une mesure ou un degré de relation entre deux variables. Un ensemble de données peut être corrélé positivement, corrélé négativement ou pas du tout corrélé. Comme un ensemble de valeurs augmente, l’autre ensemble a tendance à augmenter, on parle alors de corrélation positive.
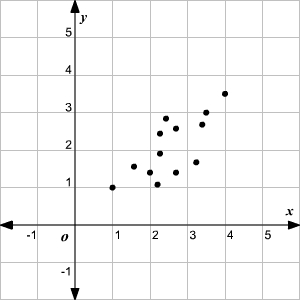
Lorsqu’un ensemble de valeurs augmente, l’autre ensemble tend à diminuer, on parle alors de corrélation négative.
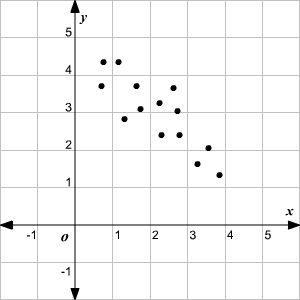
Si le changement de valeurs d’un ensemble n’affecte pas les valeurs de l’autre, alors les variables sont dites « sans corrélation » ou « corrélation nulle ». »
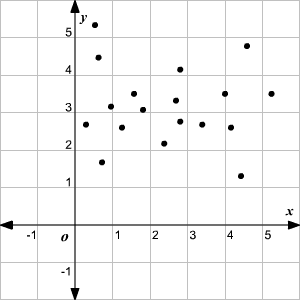
Une relation causale entre deux événements existe si l’apparition du premier provoque l’autre. Le premier événement est appelé la cause et le deuxième événement est appelé l’effet. Une corrélation entre deux variables n’implique pas de causalité. En revanche, s’il existe une relation de causalité entre deux variables, elles doivent être corrélées.
Exemple:
Une étude montre qu’il existe une corrélation négative entre l’anxiété d’un élève avant un test et le score de l’élève au test. Mais nous ne pouvons pas dire que l’anxiété provoque un score inférieur au test; il pourrait y avoir d’autres raisons — l’étudiant peut ne pas avoir bien étudié, par exemple. La corrélation ici n’implique donc pas de causalité.
Cependant, considérez la corrélation positive entre le nombre d’heures que vous passez à étudier pour un test et la note que vous obtenez au test. Ici, il y a aussi une causalité; si vous passez plus de temps à étudier, il en résulte une note plus élevée.
L’une des mesures de corrélation les plus couramment utilisées est la corrélation du moment du produit de Pearson ou le coefficient de corrélation de Pearson. Elle est mesurée à l’aide de la formule,
r x y = n ∑ x y − ∑ x ∑ y ( n ∑ x 2 − ( ∑ x ) 2 ) ( n ∑ y 2 − ( ∑ y ) 2 )
La valeur du coefficient de corrélation Pearson varie de − 1 à + 1 ou -1 indique une forte corrélation négative et + 1 indique une forte corrélation positive.