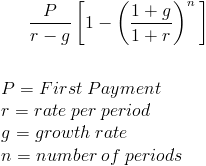
El valor actual de una fórmula de anualidad creciente calcula el valor actual de una serie de pagos periódicos futuros que crecen a una tasa proporcional. Una anualidad creciente a veces se puede denominar anualidad creciente. Un ejemplo simple de una anualidad creciente sería una persona que recibe $100 el primer año y los pagos sucesivos aumentan en un 10% por año durante un total de tres años. Este sería un recibo de $100, $110 y us $121, respectivamente.
El valor actual de una fórmula de anualidad creciente se basa en el concepto de valor temporal del dinero. La premisa de este concepto es que una cantidad específica de dinero vale más hoy que en un momento futuro.
Al igual que todas las fórmulas financieras que implican una tasa, es importante correlacionar la tasa por período con el número de períodos en el valor actual de una fórmula de anualidad creciente. Si los pagos son mensuales, entonces la tasa tendría que ser la tasa mensual.
¿Cómo se obtiene el Valor Actual de una Anualidad Creciente?
El valor actual de una anualidad creciente es la suma de los flujos de efectivo futuros. Para una anualidad en crecimiento, cada flujo de efectivo aumenta a un ritmo determinado. La fórmula para el valor actual de una anualidad creciente se puede escribir como
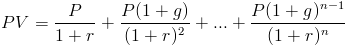
Esta fórmula es la fórmula general para sumar los flujos de efectivo futuros descontados junto con el uso de 1 + g para tener en cuenta que cada flujo de efectivo futuro aumentará a una tasa específica.
Este valor actual de una fórmula de anualidad creciente se puede reescribir como
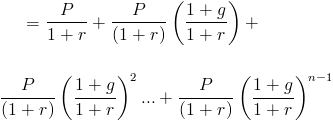
Esto se consideraría una serie geométrica donde (1+g)/(1+r) es la razón común. Al usar la fórmula de serie geométrica, el valor actual de una anualidad creciente se mostrará como
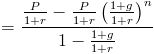
Esta fórmula se puede simplificar multiplicándola por (1+r)/(1+r), que es multiplicarla por 1. Esto cancela muchos de estos a lo largo de la fórmula, lo que deja
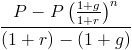
En el denominador, (1+r) – (1+g) devolverá r-g. En este punto, P y r-g se pueden factorizar, lo que conducirá al valor actual de una fórmula de anualidad creciente que se muestra en la parte superior de la página.
Volver al principio
- Fórmulas relacionadas con PV de una Anualidad Creciente
- PV de Anualidad
- PV de Perpetuidad Creciente
- Pago de Anualidad Creciente (PV)
- FV de Anualidad Creciente