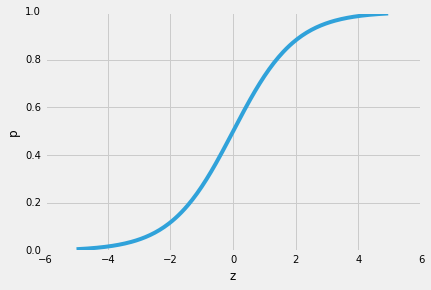
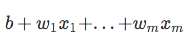Eine der schönen Eigenschaften der logistischen Regression ist also, dass die Sigmoidfunktion die bedingten Wahrscheinlichkeiten der Vorhersage, die Klassenwahrscheinlichkeiten, ausgibt. Wie funktioniert es?Beginnen wir mit dem sogenannten „Odds Ratio“ p / (1 – p), das das Verhältnis zwischen der Wahrscheinlichkeit, dass ein bestimmtes positives Ereignis eintritt, und der Wahrscheinlichkeit, dass es nicht eintritt, beschreibt – wobei sich positiv auf das „Ereignis, das wir vorhersagen wollen“ bezieht, d. H. p (y = 1 | x).
(Beachten Sie, dass die logistische Regression eine spezielle Art von Sigmoidfunktion ist, das logistische Sigmoid; andere Sigmoidfunktionen existieren, zum Beispiel die hyperbolische Tangente).
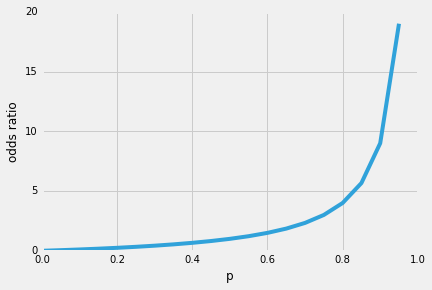
Je wahrscheinlicher es also ist, dass das positive Ereignis eintritt, desto größer ist das Quotenverhältnis.Wenn wir nun das natürliche Protokoll dieses Quotenverhältnisses, die Log-Odds- oder Logit-Funktion, verwenden, erhalten wir Folgendes
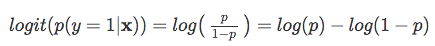
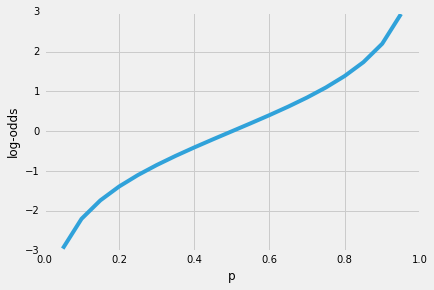
Als nächstes verwenden wir diese Log-Transformation, um die Beziehung zwischen unseren erklärenden Variablen und der Zielvariablen zu modellieren:
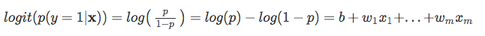
| Denken Sie daran, dass wir nicht versuchen, den richtigen Teil der obigen Gleichung vorherzusagen, da *p(y=1 | x)* uns wirklich interessiert. So, let’s take the inverse of this logit function … et viola, we get the logistic sigmoid: |
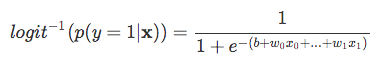
| which returns the class probabilities *p(y=1 | x)* from the inputs |