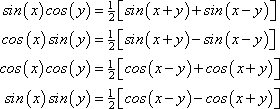Purplemath
i matematik är en ”identitet” en ekvation som alltid är sant. Dessa kan vara” trivialt ” sanna, som ”x = x” eller användbart sant, såsom Pythagoras sats ”a2 + b2 = c2” för rätt trianglar. Det finns massor av trigonometriska identiteter, men följande är de du är mest sannolikt att se och använda.
Basic & Pythagorean, Angle-Sum & -Difference, Double-Angle, Half-Angle, Sum, Product
Content Continues Below
MathHelp.com
Need a custom math course?
K12 | College | Test Prep

grundläggande och pythagoranska identiteter
affiliate
lägg märke till hur en ”co-(något)” trig-förhållandet är alltid det ömsesidiga av något ”icke-Co” – förhållande. Du kan använda detta faktum för att hjälpa dig att hålla rakt att cosecant går med sinus och secant går med cosinus.
följande (särskilt den första av de tre nedan) kallas ”pythagoranska” identiteter.
sin2 (t) + cos2 (t) = 1
tan2(t) + 1 = sec2 (t)
1 + cot2 ( t) = csc2 (t)
annons
Observera att de tre identiteterna framför allt involverar kvadrering och antalet 1. Du kan se Pythagorean-Thereom-förhållandet tydligt om du överväger enhetscirkeln, där vinkeln är t, den ”motsatta” sidan är sin(t) = y, den ”intilliggande” sidan är cos(t) = x och hypotenusen är 1.
Vi har ytterligare identiteter relaterade till Trig–kvoternas funktionella status:
sin (–t) = –sin(t)
cos (–t) = cos(t)
tan (–t) = -tan(t)
Observera särskilt att sinus och tangent är udda funktioner, är symmetriska om ursprunget, medan cosinus är en jämn funktion, är symmetrisk om ursprunget y-axeln. Det faktum att du kan ta argumentets ”minus” – tecken utanför (för sinus och tangent) eller eliminera det helt (för cosinus) kan vara till hjälp när du arbetar med komplicerade uttryck.
Vinkel-Summan och Skillnaden Identiteter
sin(α + β) = sin(α) cos(β) + cos(α) sin(β)
sin(α – β) = sin(α) cos(β) – cos(α) sin(β)
cos(α + β) = cos(α) cos(β) – sin(α) sin(β)
cos(α – β) = cos(α) cos(β) + sin(α) sin(β)
Genom det sätt, i den ovan identiteter, vinklar betecknas med grekiska bokstäver. Bokstaven A-typ, ”Kubi”, kallas” alfa”, som uttalas”AL-fuh”. Bokstaven B-typ, ”Kubi”, kallas” beta”, som uttalas”BAY-tuh”.
innehållet fortsätter under
Dubbelvinkelsidentiteter
sin(2x) = 2 sin(x) cos(x)
cos(2x) = cos2(x)-sin2(x) = 1 – 2 sin2(x) = 2 cos2(x) – 1
halv – vinkel identiteter
ovanstående identiteter kan anges igen genom att kvadrera varje sida och fördubbla alla vinkelmått. Resultaten är följande:
Affiliate

Sum Identities
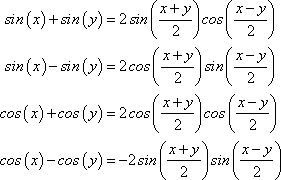
Product Identities
affiliate
du kommer att använda alla dessa identiteter, eller nästan så, för att bevisa andra trig-identiteter och för att lösa trig-ekvationer. Men om du fortsätter att studera kalkyl, var särskilt uppmärksam på de omräknade sinus-och cosinushalvvinkelidentiteterna, eftersom du kommer att använda dem mycket i integralkalkyl.
URL: https://www.purplemath.com/modules/idents.htm