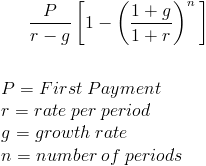
O valor presente de uma anuidade crescente fórmula calcula o atual valor de uma série de futuros pagamentos periódicos que crescer a uma taxa proporcional. Uma anuidade crescente pode por vezes ser referida como uma anuidade crescente. Um exemplo simples de uma anuidade crescente seria um indivíduo que recebe US $ 100 no primeiro ano e os pagamentos sucessivos aumentam 10% por ano para um total de três anos. Isto seria um recibo de $100, $110, e $ 121, respectivamente.
O valor atual de uma fórmula de anuidade crescente depende do conceito de valor de tempo do dinheiro. A premissa para este conceito é que uma quantidade específica de dinheiro vale mais hoje do que em um momento futuro.como todas as fórmulas financeiras que envolvem uma taxa, é importante correlacionar a taxa por período com o número de períodos no valor atual de uma fórmula de anuidade crescente. Se os pagamentos são mensais, então a taxa precisaria ser a taxa mensal.
como é derivado o valor atual de uma anuidade crescente?
o valor presente de uma anuidade crescente é a soma dos fluxos de caixa futuros. Para uma anuidade crescente, cada fluxo de caixa aumenta a uma determinada taxa. A fórmula para o valor presente de uma anuidade crescente pode ser escrito como
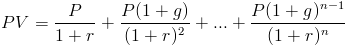
Esta é a fórmula, a fórmula geral para a soma dos fluxos de caixa futuros descontados junto com a utilização de 1 + g fator em que cada fluxo de caixa futuro aumentará a uma taxa específica.
Este valor presente de uma anuidade crescente fórmula pode ser reescrita como:
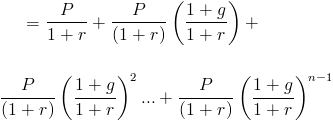
Isso seria considerado uma série geométrica, onde (1+g)/(1+r) é comum a relação. Usando a série geométrica fórmula, o valor presente de uma anuidade crescente será mostrado como
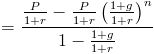
Esta fórmula pode ser simplificada, multiplicando-a por (1+r)/(1+r), que é multiplicá-lo por 1. Esta cancela muitos desses em toda a fórmula, o que deixa
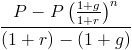
No denominador, (1+r) – (1+g) irá devolver r-g. Neste ponto, o P e r-g podem ser fatorados, que vai levar para o valor presente de uma anuidade crescente fórmula mostrada na parte superior da página.
Voltar ao Topo
- Fórmulas relacionadas ao PV de uma Crescente Anuidade
- PV de Anuidade
- PV de Crescimento Perpetuidade
- Crescente de Anuidade – Pagamento (PV)
- FV de Crescimento de Anuidade