- leerdoelen
- werk tegen de zwaartekracht
- omzetting tussen potentiële energie en kinetische energie
- met behulp van potentiële energie om berekeningen te vereenvoudigen
- Voorbeeld 1. De kracht om te stoppen met vallen
- strategie
- oplossing
- discussie
- Voorbeeld 2. Het vinden van de snelheid van een achtbaan vanaf zijn hoogte
- strategie
- oplossing voor Deel 1
- Oplossing voor Deel 2
- discussie en implicaties
- verbindingen maken: Thuisonderzoek-potentiaal omzetten in kinetische energie
- Sectieoverzicht
- conceptuele vragen
- problemen & oefeningen
- verklarende woordenlijst
- geselecteerde oplossingen voor problemen & oefeningen
leerdoelen
aan het einde van deze sectie zult u in staat zijn om:
- gravitatiepotentiaalenergie uit te leggen in termen van werk tegen de zwaartekracht.
- laat zien dat de potentiële gravitatieenergie van een object met massa M op hoogte h op aarde wordt gegeven door PEg = mgh.
- laat zien hoe kennis van de potentiële energie als functie van de positie kan worden gebruikt om berekeningen te vereenvoudigen en fysische verschijnselen te verklaren.
werk tegen de zwaartekracht
traplopen en hijsobjecten is werk in zowel wetenschappelijke als alledaagse zin—het is werk tegen de zwaartekracht. Als er werk is, is er een transformatie van energie. Het werk tegen de zwaartekracht gaat naar een belangrijke vorm van opgeslagen energie die we in deze sectie zullen onderzoeken.

figuur 1. (a) het werk dat wordt verricht om het gewicht op te heffen wordt opgeslagen in het massa-aarde-systeem als potentiële gravitatieenergie. (B) als het gewicht naar beneden beweegt, wordt deze potentiële gravitatieenergie overgebracht naar de koekoeksklok.
laten we het werk berekenen dat wordt verricht bij het optillen van een voorwerp met massa m door een hoogte h, zoals in Figuur 1. Als het object recht omhoog wordt gehesen met constante snelheid, dan is de kracht die nodig is om het op te tillen gelijk aan zijn gewicht mg. Het werk aan de massa is dan W = Fd = mgh. We definiëren dit als de gravitatiepotentiaal energie (PEg) die in (of gewonnen wordt door) het object-aarde systeem. Deze energie wordt geassocieerd met de staat van scheiding tussen twee objecten die elkaar aantrekken door de zwaartekracht. Voor het gemak noemen we dit de PIN die het object heeft gewonnen, erkennend dat dit energie is die is opgeslagen in het zwaartekrachtveld van de aarde. Waarom gebruiken we het woord “systeem”? Potentiële energie is een eigenschap van een systeem in plaats van van een enkel object—vanwege zijn fysieke positie. Het gravitatiepotentieel van een object is te wijten aan zijn positie ten opzichte van de omgeving binnen het Aarde-objectsysteem. De kracht die op het object wordt uitgeoefend is een externe kracht, van buiten het systeem. Als het positieve werk doet, verhoogt het de potentiële gravitatieenergie van het systeem. Omdat de potentiële gravitatieenergie afhankelijk is van de relatieve positie, hebben we een referentieniveau nodig waarop de potentiële energie gelijk is aan 0. We kiezen meestal voor dit punt om het aardoppervlak te zijn, maar dit punt is willekeurig; wat belangrijk is, is het verschil in gravitatiepotentiaal energie, omdat dit verschil betrekking heeft op het verrichte werk. Het verschil in gravitatiepotentiaalenergie van een object (in het Aarde-objectsysteem) tussen twee sporten van een ladder zal voor de eerste twee sporten hetzelfde zijn als voor de laatste twee sporten.
omzetting tussen potentiële energie en kinetische energie
potentiële Gravitatieenergie kan worden omgezet in andere vormen van energie, zoals kinetische energie. Als we de massa vrijgeven, zal de gravitatiekracht een hoeveelheid werk doen die gelijk is aan mgh, waardoor de kinetische energie met dezelfde hoeveelheid wordt verhoogd (door de werk-energiestelling). We zullen het nuttiger vinden om alleen de conversie van PEg naar KE te overwegen zonder expliciet rekening te houden met de tussenstap van het werk. (Zie Voorbeeld 2.) Deze snelkoppeling maakt het gemakkelijker om problemen op te lossen met behulp van energie (indien mogelijk) in plaats van expliciet met behulp van krachten.
preciezer definiëren we de verandering in gravitatiepotentiaal energie ΔPEg als ΔPEg = mgh, waarbij we, voor de eenvoud, de verandering in hoogte met h aangeven in plaats van de gebruikelijke Δh. Merk op dat h positief is wanneer de uiteindelijke hoogte groter is dan de initiële hoogte, en vice versa. Bijvoorbeeld, als een 0.500-kg massa opgehangen aan een koekoeksklok wordt verhoogd 1.00 m, dan is de verandering in de gravitationele potentiële energie is
\begin{array}{lll}mgh&&(0.500\text{ kg})(9.80\text{ m/s}^2)(1.00\text{ m})\\\text{ }&&4.90\text{ kg}\cdot\text{m}^2\text{/s}^2=4.90\text{ J}\end{array}\\
er rekening mee dat de eenheden van gravitationele potentiële energie blijken te zijn joules, hetzelfde als voor het werk en andere vormen van energie. Als de klok loopt, wordt de massa verlaagd. We kunnen de massa zien als het geleidelijk opgeven van zijn 4.90 J van de potentiële gravitatieenergie, zonder direct rekening te houden met de zwaartekracht die het werk doet.
met behulp van potentiële energie om berekeningen te vereenvoudigen

Figuur 2. De verandering in de potentiële gravitatieenergie (ΔPEg) tussen de punten A en B is onafhankelijk van het pad.
de vergelijking ΔPEg = mgh geldt voor elk pad met een hoogteverandering van h, niet alleen wanneer de massa recht omhoog wordt opgetild. (Zie Figuur 2.) Het is veel gemakkelijker om mgh (een eenvoudige vermenigvuldiging) te berekenen dan om het werk te berekenen langs een ingewikkeld pad. Het idee van gravitatiepotentiaal energie heeft het dubbele voordeel dat het zeer breed toepasbaar is en het maakt berekeningen gemakkelijker.
van nu af aan zullen we ervan uitgaan dat elke verandering in verticale positie h van een massa m gepaard gaat met een verandering in de potentiële gravitatieenergie mgh, en we zullen de gelijkwaardige, maar moeilijkere taak van het berekenen van werk gedaan door of tegen de gravitatiekracht vermijden.
ΔPEg = mgh voor elk pad tussen de twee punten. Zwaartekracht is een van een kleine klasse van krachten waar het werk gedaan door of tegen de kracht alleen afhangt van de begin-en eindpunten, niet op het pad ertussen.
Voorbeeld 1. De kracht om te stoppen met vallen
a 60.0-kg persoon springt op de vloer vanaf een hoogte van 3,00 m. als hij stijf landt (met zijn kniegewrichten samendrukken met 0,500 cm), bereken de kracht op de kniegewrichten.
strategie
de energie van deze persoon wordt in deze situatie op nul gebracht door het werk dat op hem wordt gedaan door de vloer als hij stopt. De eerste pin wordt omgezet in KE als hij valt. Het werk van de vloer reduceert deze kinetische energie tot nul.
oplossing
het werk dat aan de persoon door de vloer wordt gedaan bij het stoppen wordt gegeven door W = Fd cos θ = −Fd, met een minteken omdat de verplaatsing tijdens het stoppen en de kracht van de vloer in tegengestelde richtingen zijn (cos θ = cos 180º = -1). De vloer verwijdert energie uit het systeem, dus het doet negatief werk.
de kinetische energie die de persoon heeft bij het bereiken van de vloer is de hoeveelheid potentiële energie die verloren gaat door vallen door hoogte h: KE = −ΔPEg = −mgh.
de afstand d dat de knieën van de persoon buigen is veel kleiner dan de hoogte h van de val, dus de extra verandering in zwaartekracht potentiële energie tijdens de knie bocht wordt genegeerd.
het werk dat door de vloer op de persoon wordt gedaan, stopt de persoon en brengt de kinetische energie van de persoon op Nul: W = – KE = mgh.
Het combineren van deze vergelijking met de uitdrukking voor W geeft-Fd = mgh.
eraan herinnerend dat h negatief is omdat de persoon viel, wordt de kracht op de kniegewrichten gegeven door
\displaystyle{F}=-\frac{mgh}{d}=-\frac{\left(60.0 \ text{ kg}\right)\left(9.80\text{ m/s}^2\right)\left(-3.00\text{ m}\right)}{5.00\times10^{-3}\text{ m}}=3.53\times10^5\text{ N}\ \
discussie
zo ‘ n grote kracht (500 keer meer dan het gewicht van de persoon) over de korte inslagtijd is genoeg om botten te breken. Een veel betere manier om de schok te verzachten is door de benen te buigen of op de grond te rollen, waardoor de tijd waarin de kracht werkt wordt verhoogd. Een buigbeweging van 0,5 m levert op deze manier een kracht op die 100 keer kleiner is dan in het voorbeeld. Het hoppen van een kangoeroe toont deze methode in actie. De kangoeroe is het enige grote dier dat hoppen gebruikt voor beweging, maar de schok bij het hoppen wordt opgevangen door het buigen van zijn achterpoten in elke sprong. (Zie Figuur 3.)

Figuur 3. Het werk van de grond op de kangoeroe reduceert zijn kinetische energie tot nul als hij landt. Echter, door de kracht van de grond op de achterpoten over een langere afstand toe te passen, wordt de impact op de botten verminderd. (credit: Chris Samuel, Flickr)
Voorbeeld 2. Het vinden van de snelheid van een achtbaan vanaf zijn hoogte
- Wat is de eindsnelheid van de achtbaan zoals weergegeven in Figuur 4 als hij begint met rust op de top van de 20,0 m hoge heuvel en het werk door wrijvingskrachten te verwaarlozen is?
- Wat is het eindtoerental (ook in de veronderstelling van verwaarloosbare wrijving) als het begintoerental 5,00 m/s is?
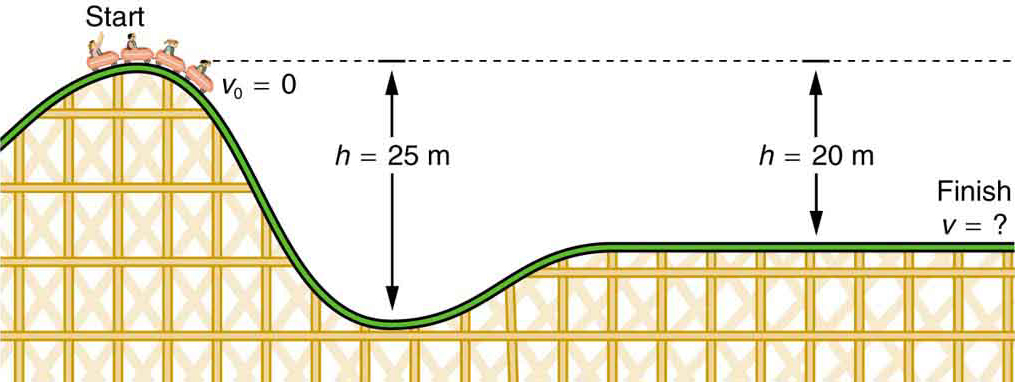
Figuur 4. De snelheid van een achtbaan neemt toe naarmate de zwaartekracht hem naar beneden trekt en is het grootst op het laagste punt. Gezien in termen van energie, wordt de gravitatiepotentiaal van het achtbaan-aarde systeem omgezet in kinetische energie. Als het werk door wrijving verwaarloosbaar is, wordt alle ΔPEg omgezet in KE.
strategie
De Achtbaan verliest potentiële energie als hij bergafwaarts gaat. We verwaarlozen wrijving, zodat de resterende kracht die door het spoor wordt uitgeoefend de normale kracht is, die loodrecht staat op de bewegingsrichting en geen werk doet. Het netwerk aan de achtbaan wordt dan door zwaartekracht alleen gedaan. Het verlies van gravitatiepotentiaal energie uit het bewegen naar beneden door een afstand h is gelijk aan de winst in kinetische energie. Dit kan in vergelijkingsvorm worden geschreven als-ΔPEg = ΔKE. Met behulp van de vergelijkingen voor PEg en KE, kunnen we oplossen voor de uiteindelijke snelheid v, dat is de gewenste hoeveelheid.
oplossing voor Deel 1
Hier is de initiële kinetische energie nul, zodat \Delta \ text{KE} = \frac{1}{2}mv^2\\. De vergelijking voor verandering in potentiële energie stelt dat ΔPEg = mgh. Aangezien h in dit geval negatief is, zullen we dit herschrijven als ΔPEg = −mg|h| om het minteken duidelijk weer te geven. Zo wordt-ΔPEg = ΔKE mg|h|=\frac{1}{2}{mv}^2\\.
oplossend voor v, vinden we dat massa annuleert en dat v=\sqrt{2g|h|}\\.
het Vervangen van bekende waarden,
\begin{array}{lll}v&&\sqrt{2\left(9.80\text{ m/s}^2\right)\left(20.0\text{ m}\right)}\\\text{ }&&19.8\text{ m/s}\end{array}\\
Oplossing voor Deel 2
Opnieuw −ΔPEg = ΔKE. In dit geval is er initiële kinetische energie, dus
\Delta\text{KE}=\frac{1}{2}mv^2-\frac{1}{2}mv_0^2\\.
dus mg / h/= \ frac{1}{2}mv^2- \ frac{1}{2}mv_0^2\\.
het herschikken geeft \frac{1}{2}mv^2 = mg|h / +\frac{1}{2}mV+0^2\\.
Dit betekent dat de uiteindelijke kinetische energie de som is van de initiële kinetische energie en de potentiële zwaartekrachtenergie. Massa weer annuleert, en v=\sqrt{2g|h / +v_0^2}\\.
deze vergelijking lijkt sterk op de kinematica vergelijking v=\sqrt{v_0^2+2ad}\\, maar is algemener—de kinematica vergelijking is alleen geldig voor constante versnelling, terwijl onze vergelijking hierboven geldig is voor elk pad, ongeacht of het object beweegt met een constante versnelling. Nu, de vervanging van bekende waarden geeft
\begin{array}{lll}v&&\sqrt{2\left(9.80\text{ m/s}^2\right)\left(20.0\text{ m}\right)+\left(5.00\text{ m/s}\right)^2}\\\text{ }&&20.4 \ text{ m/s}\end{array}\\
discussie en implicaties
merk eerst op dat massa annuleert. Dit is vrij consistent met observaties gemaakt bij vallende objecten dat alle objecten in hetzelfde tempo vallen als de wrijving te verwaarlozen is. Ten tweede wordt alleen rekening gehouden met de snelheid van de achtbaan; er is geen informatie over de richting op enig punt. Dit onthult een andere algemene waarheid. Wanneer de wrijving verwaarloosbaar is, hangt de snelheid van een vallend lichaam alleen af van zijn oorspronkelijke snelheid en hoogte, en niet van zijn massa of het gekozen pad. Bijvoorbeeld, de achtbaan zal dezelfde eindsnelheid hebben of het nu 20,0 m recht naar beneden valt of een ingewikkelder pad neemt zoals die in de figuur. Ten derde, en misschien onverwacht, de eindsnelheid in deel 2 is groter dan in deel 1, maar met veel minder dan 5,00 m/s. tot slot, merk op dat de snelheid kan worden gevonden op elke hoogte langs de weg door simpelweg het gebruik van de juiste waarde van h op het punt van belang.
we hebben gezien dat werk gedaan door of tegen de gravitatiekracht alleen afhangt van de begin-en eindpunten, en niet van het pad ertussen, waardoor we het vereenvoudigende concept van gravitatiepotentiaal-energie kunnen definiëren. We kunnen hetzelfde doen voor een paar andere krachten, en we zullen zien dat dit leidt tot een formele definitie van de wet van behoud van energie.
verbindingen maken: Thuisonderzoek-potentiaal omzetten in kinetische energie
men kan de conversie van potentiële gravitatieenergie in kinetische energie bestuderen in dit experiment. Gebruik op een glad, vlak oppervlak een liniaal van het soort dat een groef over zijn lengte en een boek heeft om een helling te maken (zie Figuur 5). Plaats een knikker op de 10-cm positie op de liniaal en laat het de liniaal naar beneden rollen. Wanneer het raakt het niveau oppervlak, meet de tijd die nodig is om te rollen een meter. Plaats nu het marmer op de 20-cm en de 30-cm posities en meet opnieuw de tijden die nodig zijn om 1 m op het vlakke oppervlak te rollen. Vind de snelheid van het marmer op het vlakke oppervlak voor alle drie de posities. Plotsnelheid kwadraat versus de afstand afgelegd door het marmer. Wat is de vorm van elke plot? Als de vorm een rechte lijn is, toont de plot aan dat de kinetische energie van het marmer aan de onderkant evenredig is met de potentiële energie op het loslaatpunt.

Figuur 5. Een marmer rolt een liniaal naar beneden, en de snelheid ervan op het vlakke oppervlak wordt gemeten.
Sectieoverzicht
- werk tegen de zwaartekracht bij het optillen van een object wordt potentiële energie van het object-aarde-systeem.
- de verandering in de potentiële gravitatieenergie, ΔPEg, is ΔPEg = mgh, waarbij h de toename in hoogte is en g de versnelling als gevolg van de zwaartekracht.
- de potentiële gravitatieenergie van een object in de buurt van het aardoppervlak is toe te schrijven aan zijn positie in het massa-aardsysteem. Alleen verschillen in gravitatiepotentiaal energie, ΔPEg, hebben een fysische betekenis.
- als een object zonder wrijving afdaalt, verandert zijn gravitatiepotentiaal energie in kinetische energie die overeenkomt met toenemende snelheid, zodat ΔKE = −ΔPEg
conceptuele vragen
- In Voorbeeld 2 hebben we de eindsnelheid berekend van een achtbaan die 20 m hoog afdaalde en een beginsnelheid van 5 m/s bergafwaarts had. Stel dat de achtbaan in plaats daarvan een beginsnelheid van 5 m/s bergop had, en hij ging bergop, stopte en rolde dan terug naar een laatste punt 20 m onder de start. We zouden in dat geval vinden dat het dezelfde eindsnelheid had. Leg uit in termen van energiebesparing.
- hangt het werk dat u doet aan een boek wanneer u het op een plank tilt af van het pad dat u hebt genomen? Over de tijd? Op de hoogte van de plank? Op de massa van het boek?
problemen & oefeningen
- een waterkrachtcentrale (zie Figuur 6) Zet de potentiële zwaartekrachtenergie van water achter een dam om in elektrische energie. (A) Wat is de potentiële gravitatieenergie ten opzichte van de generatoren van een meer van volume 50.0 km3 (massa = 5,00 × 1013 kg), gezien het feit dat het meer een gemiddelde hoogte van 40,0 m boven de generatoren heeft? (B) vergelijk dit met de energie opgeslagen in een 9-megaton fusiebom.

Figuur 6. Hydro-elektrische faciliteit (credit: Denis Belevich, Wikimedia Commons)
- (a) hoeveel gravitatiepotentiaal energie (ten opzichte van de grond waarop het is gebouwd) is opgeslagen in de Grote Piramide van Cheops, gezien het feit dat de massa ongeveer 7 × 109 kg is en het middelpunt van de massa 36 is.5 m boven de omringende grond? (b) Hoe verhoudt deze energie zich tot de dagelijkse voedselinname van een persoon?stel dat een kookaburra van 350 g (een grote ijsvogel) een slang van 75 g oppakt en 2,5 m van de grond opheft tot een tak. (a) hoeveel werk heeft de vogel gedaan op de slang? (b) hoeveel werk heeft het gedaan om zijn eigen centrum van Massa naar de tak te verhogen?
- in Voorbeeld 2 vonden we dat de snelheid van een achtbaan die 20,0 m afdaalde slechts iets hoger was wanneer hij een beginsnelheid van 5,00 m/s had dan toen hij vanuit de rust begon. Dit betekent dat ΔPE >> KEi. Bevestig deze verklaring door de verhouding ΔPE tot KEi te nemen. (Merk op dat massa annuleert.)
- een 100 g speelgoedauto wordt aangedreven door een samengeperste veer die hem in beweging zet. De auto volgt het gebogen spoor in Figuur 7. Laat zien dat de eindsnelheid van de speelgoedauto 0,687 m/s is als de beginsnelheid 2,00 m/s is en hij de wrijvingsloze helling oploopt, met een hoogte van 0,180 m.

Figuur 7. Een speelgoedauto rijdt over een hellend spoor. (credit: Leszek Leszczynski, Flickr)
- in een afdaling ski race, verrassend genoeg, weinig voordeel wordt opgedaan door het krijgen van een running start. (Dit komt omdat de initiële kinetische energie klein is in vergelijking met de winst in gravitationele potentiële energie op zelfs kleine heuvels.) Om dit aan te tonen, vinden de uiteindelijke snelheid en de tijd die nodig is voor een skiër die 70,0 m skiën langs een 30º helling zonder wrijving: (a) vanaf rust. (B) beginnend met een beginsnelheid van 2,50 m/s. (c) verbaast het antwoord u? Bespreek waarom het nog steeds voordelig is om een running start te krijgen in zeer concurrerende evenementen.
verklarende woordenlijst
gravitatiepotentiaal energie: de energie die een object heeft vanwege zijn positie in een gravitatieveld
geselecteerde oplossingen voor problemen & oefeningen
1. (a) 1,96 × 1016 J; (b) de verhouding tussen de potentiële gravitatieenergie in het meer en de energie die in de bom is opgeslagen, is 0,52. Dat wil zeggen, de energie opgeslagen in het meer is ongeveer de helft van die in een 9-megaton fusiebom.
3. (a) 1,8 J; (b) 8,6 J
5. {v}_{F} = \sqrt{2gh + {v_0}^2}=\sqrt{2\left (9.80\text{ m/s}^2\right)\left(-0.180\text{ m}\right)+\left(2.00\text{ m/s}\right)^2}=0,687 \ text{ m/s}\\