Atomic Orbitals
een orbitaal is de kwantummechanische verfijning van Bohr ‘ s Baan. In tegenstelling tot zijn concept van een eenvoudige cirkelbaan met een vaste straal, zijn orbitalen wiskundig afgeleide gebieden van de ruimte met verschillende waarschijnlijkheid van het hebben van een elektron.
een manier om elektronenkansdistributies weer te geven werd geïllustreerd in Figuur 6.5.2 voor de 1s-baan van waterstof. Omdat Ψ2 de kans geeft om een elektron te vinden in een gegeven ruimtevolume (zoals een kubieke picometer), is een plot van Ψ2 versus afstand van de kern (r) een plot van de kansdichtheid. De 1s orbitaal is sferisch symmetrisch, dus de kans op het vinden van een 1s elektron op een bepaald punt hangt alleen af van de afstand tot de kern. De waarschijnlijkheidsdichtheid is het grootst bij r = 0 (bij de kern) en neemt gestaag af met toenemende afstand. Bij zeer grote waarden van r is de kansdichtheid van het elektron zeer klein, maar niet nul.
daarentegen kunnen we de radiale waarschijnlijkheid (de kans om een 1s elektron te vinden op een afstand r van de kern) berekenen door de waarschijnlijkheid van een elektron op alle punten op een reeks van x Sferische schillen met straal r1, r2, r3,…, rx − 1, rx bij elkaar op te tellen. In feite verdelen we het atoom in zeer dunne concentrische schelpen, net als de lagen van een UI (Deel (A) in Figuur \(\Paginindex{1}\)), en berekenen we de kans op het vinden van een elektron op elke bolvormige schelp. Bedenk dat de elektronenkansdichtheid het grootst is bij r = 0 (deel (b) in Figuur \(\Paginindex{1}\)), zodat de dichtheid van de punten het grootst is voor de kleinste bolvormige schalen in deel (a) in Figuur \(\Paginindex{1}\). Daarentegen is het oppervlak van elke bolvormige schil gelijk aan 4nr2, wat zeer snel toeneemt met toenemende r (deel (c) in Figuur \(\Paginindex{1}\)). Omdat het oppervlak van de sferische schelpen sneller toeneemt met toenemende r dan de elektronenkansdichtheid afneemt, heeft de plot van de radiale waarschijnlijkheid een maximum op een bepaalde afstand (Deel (d) in Figuur \(\Paginindex{1}\)). Het belangrijkste is dat wanneer r heel klein is, het oppervlak van een bolvormige schil zo klein is dat de totale kans op het vinden van een elektron dicht bij de kern erg laag is; bij de kern verdwijnt de elektronkans (Deel (d) in Figuur \(\Paginindex{1}\)).

Voor het waterstofatoom vindt de piek in de radiale waarschijnlijkheidsperceel plaats bij r = 0,529 Å (52,9 pm), wat precies de straal is die door Bohr wordt berekend voor de N = 1 baan. De meest waarschijnlijke straal verkregen uit de kwantummechanica is dus identiek aan de straal berekend door de klassieke mechanica. In Bohr ‘ s model, echter, werd aangenomen dat het elektron op deze afstand 100% van de tijd, terwijl in de kwantummechanische Schrödinger model, het is op deze afstand slechts een deel van de tijd. Het verschil tussen de twee modellen is toe te schrijven aan het golfachtige gedrag van het elektron en het Heisenberg onzekerheid Principe.
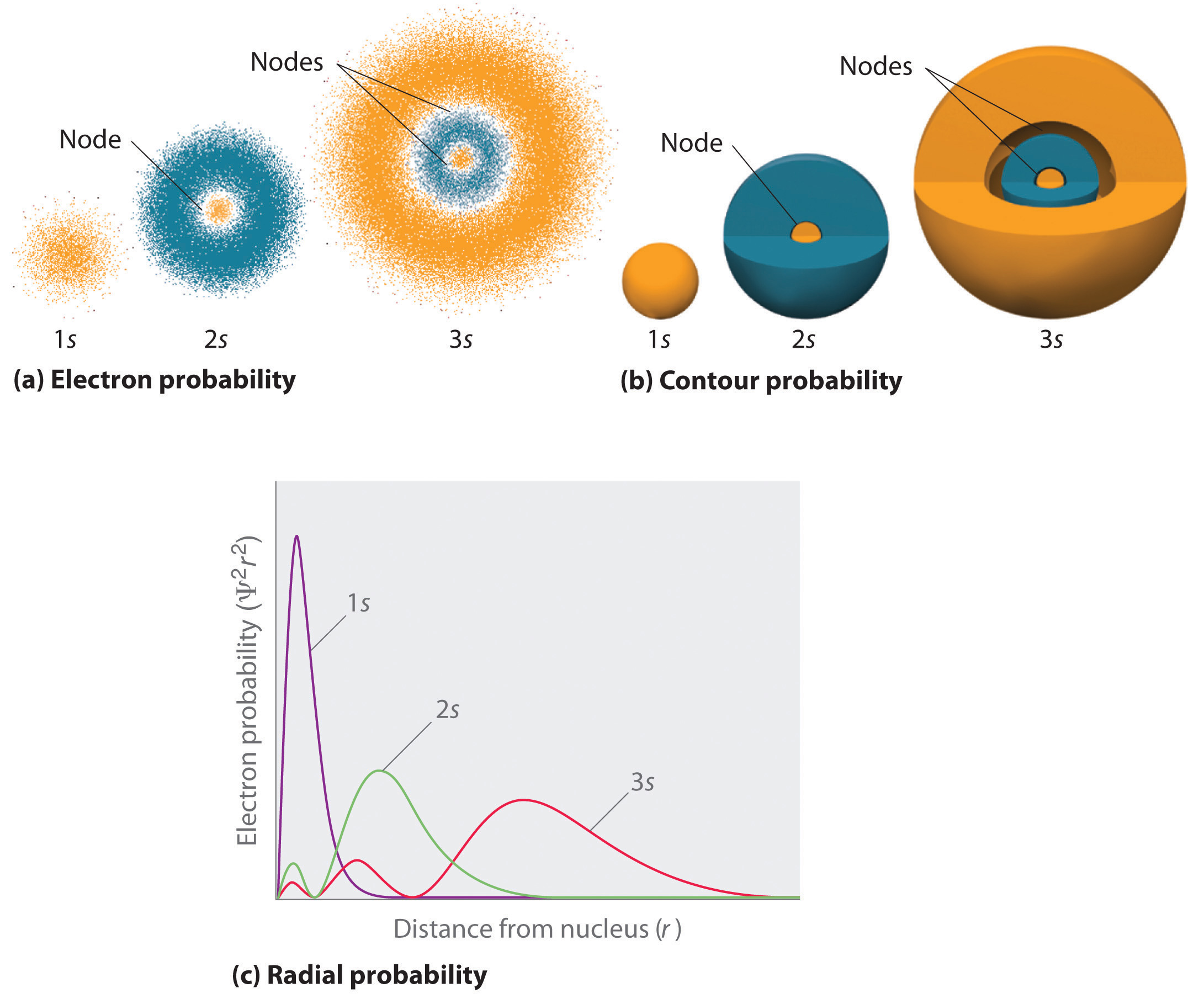
figuur \(\Pagindex{2}\) vergelijkt de elektronenkansdichtheden voor de waterstof 1s, 2s en 3s orbitalen. Merk op dat alle drie sferisch symmetrisch zijn. Voor de 2s en 3s orbitalen echter (en voor alle andere s orbitalen ook), valt de elektronenkansdichtheid niet soepel af bij toenemende r. in plaats daarvan worden een reeks minima en maxima waargenomen in de radiale waarschijnlijkheidsgrafieken (deel (c) in Figuur \(\Paginindex{2}\)). De minima komen overeen met sferische knooppunten (gebieden met een elektronenkans van nul), die worden afgewisseld met sferische gebieden met een elektronenkans van niet nul.