Detta är en pågående översyn av denna sida. Det kan skilja sig från den senast accepterade revisionen, som godtogs den 13 januari 2011.

den molära volymen (symbol Vm) för ett ämne är den volym som upptas av en mol av ämnet vid en givet temperatur och tryck. Den är lika med ämnets molekylmassa (M) dividerat med dess densitet (ci) vid given temperatur och tryck:

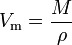
den har en SI-enhet på kubikmeter per mol (m3/mol). Molära volymer uttrycks emellertid ofta som kubikmeter per 1000 mol (m3/kmol) eller kubiska decimeter per mol (dm3/mol) för gaser och som centimeter per mol (cm3/mol) för vätskor och fasta ämnen.

om ett ämne är en blandning innehållande n-komponenter beräknas molvolymen med användning av:

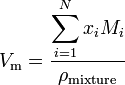
där x i är molfraktionen för ith-komponenten, M i är molekylmassan för ith-komponenten och pmixture är blandningstätheten vid given temperatur och tryck.

När du anger numeriska värden för molar volym är det viktigt att också ange de givna förhållandena för temperatur och tryck. Annars är de numeriska värdena meningslösa.

ideala gaser

den ideala gaslagen ekvationen kan ordnas om för att ge detta uttryck för den molära volymen av en idealisk gas:

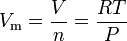
var i SI-enheter:

P

= gasen absolut tryck, i pa

n

= antal mol, i mol

VM

= gasmolvolymen, i M3/mol

t

= gasens absoluta temperatur, i k

r

= den universella gaslagskonstanten på 8.314472 m3·pa·mol-1·K-1

var i amerikanska sedvanliga enheter:

P

= gasens absoluta Tryck, i psia

n

= antal mol, i lb-mol

Vm

= gasmolvolymen, i ft3/lb-mol

T

= gasens absoluta temperatur, i grader Rankine (kub R)

r

= den universella gaslagskonstanten på 10.7316 ft3·psia·lb-mol-l·kubi r-1

exempel beräkningar av ideala gasmolära volymer:

• i Si-metriska enheter:

VM = 8.314472 273.15 / 101,325 = 0.022414 m3/mol vid 0 kg C och 101 325 pa absolut tryck = 22.414 m3/kmol vid 0 kg c (273.15 k) och 101.325 kPa absoluttryck Vm = 8.314472 × 273.15 / 100,000 = 0.022711 m3/kmol vid 0 °C och 100 000 Pa det absoluta trycket = 22.711 m3/kmol vid 0 °C (273.15 K) och 100 kPa absoluttryck

• I sedvanliga USA-enheter:

Vm = 10.7316 × 519.67 / 14.696 = 379.48 ft3/lb-mol vid 60 °F (519.67 °R) och 14.696 psia

Anteckningar:

• lb-mol är en förkortning för kilo-mol
• °R grader Rankine (absolut temperatur skala) och °F grader Fahrenheit (en temperatur skala).
• r = f + 459.67
• den tekniska litteraturen kan vara förvirrande eftersom vissa författare ofta misslyckas med att förklara om de använder universal gas law constant R, som gäller för någon idealgas, eller om de använder den specifika Gas law constant Rs, som endast gäller för en specifik individuell gas. Förhållandet mellan de två konstanterna är Rs = R / M där M är gasens molekylmassa.

verkliga gaser

verkliga gaser är de gaser som inte uppvisar idealiskt gasbeteende. För sådana gaser är den enklaste metoden att bestämma molära volymer genom att använda komprimeringsfaktorer som i följande uttryck:

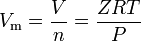
där Z är gaskompressibilitetsfaktorn, som är en användbar termodynamisk egenskap för att modifiera den ideala gaslagen för att redogöra för beteende hos verkliga gaser. Ovanstående ekvation är i grunden en enkel tillståndsekvation (EOS). Den största begränsningen av denna tillståndsekvation är att gaskompressibilitetsfaktorn, Z, inte är en konstant utan varierar från en gas till en annan såväl som med temperaturen och trycket hos den aktuella gasen.

mer exakta värden på reala gasmolära volymer kan erhållas genom att använda tillståndsekvationer såsom van der Waals ekvation utvecklad 1873, Redlich-Kwong ekvation utvecklad 1949, Soave-Redlich-Kwong ekvation utvecklad 1972 och Peng-Robinson ekvation utvecklad 1976.

en del innehåll på denna sida kan tidigare ha dykt upp på Citizendium.