Konigsberg är en stad på Pregerfloden, som på 18-taletvar en tysk stad, men nu är ryska. Inom staden finns tvåriveröarna som är anslutna till bankerna med sju broar (som visas nedan).

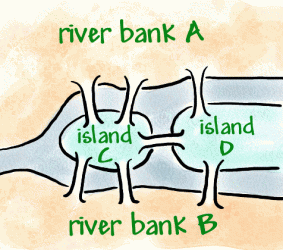
det blev en tradition att försöka gå runt staden på ett sätt sombara korsade varje bro en gång, men det visade sig vara ett svårtproblem. Leonhard Euler, en schweizisk matematiker i tjänsten avden ryska kejsarinnan Catherine The Great, hörde om problemet.År 1736 bevisade Euler att promenaden inte var möjlig att göra. Hanvisade detta genom att uppfinna ett slags diagram som kallas ett nätverk, detbestår av hörn (prickar där linjer möts) och bågar(linjer).

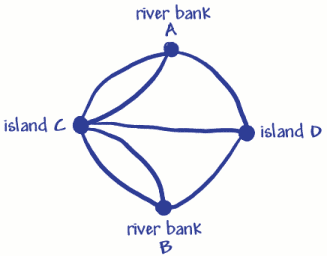
han använde fyra punkter (hörn) för de två flodbankerna och twoislands. Dessa har markerats A, B och C, D. De sju linjerna(bågarna) är de sju broarna. Du kan se att 3 broar (bågar)går med i riverbank A och 3 går med i riverbank B. 5 broar (bågar)går med i island C och 3 går med i island D. Det betyder att allavertices har ett udda antal bågar, så de kallas oddvertices. (Ett jämnt vertex måste ha ett jämnt antal bågaransluter sig till det).
kom ihåg att problemet var att resa runt staden korsar varjebro bara en gång. På Eulers nätverk innebar detta att spåra över varjearc bara en gång och besökte alla hörn. Euler bevisade att det inte kunde göras för att han utarbetade det för att ha ett udda vertex som du skulle behöva börja eller avsluta resan vid det vertexet. (Fundera).Eftersom det bara kan finnas en början och en ände, kan det bara vara två udda hörn om du bara kommer att kunna spåra över eacharc en gång. Eftersom broproblemet har 4 udda hörn, är det baraär inte möjligt att göra! Vad händer om det inte finns några udda hörn påalla? Kan detta nätverk spåras?

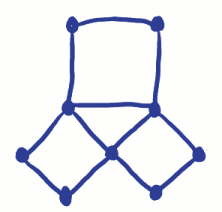
uppfinningen av nätverk började en helt ny typ av geometri kalladtopologi. Topologi används nu på många sätt, inklusive för planeringoch kartläggning av järnvägsnät. (Ahhh! Tåg var tvungna att komma in idet….)