Algebra är jättekul – du får lösa pussel!
ett pussel
vad är det saknade numret?
| − | 2 | = | 4 |
ok, svaret är 6, eller hur? Eftersom 6 – 2 = 4. Enkla saker.
Tja, i Algebra använder vi inte tomma rutor, vi använder en bokstav (vanligtvis en x eller y, men någon bokstav är bra). Så vi skriver:
| x | − | 2 | = | 4 |
det är verkligen så enkelt. Brevet (i detta fall ett x) betyder bara ”vi vet inte detta ännu”, och kallas ofta det okända eller variabeln.
och när vi löser det skriver vi:
| x | = | 6 |
Why Use a Letter?
| Because: | |
| it is easier to write ”x” than drawing empty boxes (and easier to say ”x” than ”the empty box”). | |
| om det finns flera tomma rutor (flera ”okända”) kan vi använda en annan bokstav för var och en. |
så x är helt enkelt bättre än att ha en tom ruta. Vi försöker inte göra ord med det!
och det behöver inte vara x, det kan vara y eller w … eller någon bokstav eller symbol vi gillar.
hur man löser
Algebra är precis som ett pussel där vi börjar med något som ”x − 2 = 4” och vi vill sluta med något som ”x = 6”.
men istället för att säga ”uppenbarligen x=6”, använd den här snygga steg-för-steg-metoden:
- ta reda på vad du ska ta bort för att få ”x = …”
- ta bort det genom att göra motsatsen (lägga till är motsatsen till subtraktion)
- gör det till båda sidor
Här är ett exempel:
för att ta bort
”-2”
![]()
för att ta bort det, gör
motsatsen, i
detta fall lägg till 2
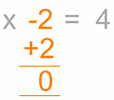
gör det till
båda sidor
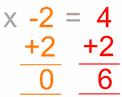
vilket är …
![]()
löst!
![]()
varför lade vi till 2 på båda sidor?
för att ”hålla balansen”…
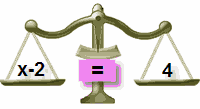
Lägg till 2 till vänster

ur balans!
Lägg till 2 till höger också
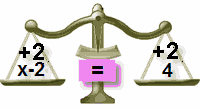
i balans igen
kom bara ihåg detta:
för att hålla balansen, vad vi gör på ena sidan av ”=”
vi borde också göra på andra sidan!
See this in action at the Algebra Balance Animation.
Another Puzzle
Solve this one:
| x | + | 5 | = | 12 |
What we want is an answer like ”x = …”,
but the +5 is in the way of that!
vi kan avbryta +5 med en -5 (eftersom 5-5=0)
prova själv
öva nu på det här enkla Algebra-kalkylbladet och kontrollera sedan dina svar. Försök att använda stegen vi har visat dig här, snarare än att bara gissa!
prova frågorna nedan och läs sedan introduktion till algebra-multiplikation