Az exponenciális függvény megértése után a következő cél a természetes logaritmus.

tekintettel arra, hogy a természetes naplót hogyan írják le a matematikai könyvekben, kevés “természetes” van róla: a $e^x$ inverzeként definiálják, ami már elég furcsa exponens.

de van egy friss, intuitív magyarázat: a természetes napló megadja a szükséges időt egy bizonyos növekedési szint eléréséhez.

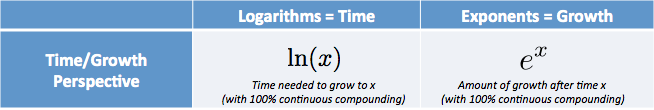
tegyük fel, hogy van egy befektetés gumicukor (ki nem?) évi 100% – os kamattal, folyamatosan növekszik. Ha azt szeretnénk, 10x növekedés, feltételezve, folyamatos összetételű, azt várni csak $\ln(10)$ vagy 2.302 év. Nem értem, miért csak néhány évig tart, hogy 10x növekedést érjen el? Nem értem, miért nem 1, 2, 4, 8 a minta? További információ e.

E és a természetes napló ikrek:

• $e^x$ az az összeg, amelyet az 1.0 és folyamatosan növekszik $x$ időegység
• $\ln(x)$ (természetes logaritmus) az idő, hogy elérje összeg $x$, feltételezve, hogy folyamatosan nőtt 1.0

nem túl rossz, jobb? Míg a matematikusok tülekedés, hogy megadja a hosszú, technikai magyarázat, nézzük belevetik magukat az intuitív.

E a növekedésről szól

az e szám a folyamatos növekedésről szól. Mint láttuk Legutóbb, $e^x$ lehetővé teszi számunkra merge arány és idő: 3 év 100% – os növekedés ugyanaz, mint 1 év 300% – os növekedés, amikor folyamatosan össze.

a sebesség és az idő bármely kombinációját (50% 4 évre) alkalmazhatjuk, és a kényelem érdekében 100% – ra konvertálhatjuk az arányt (100% – ot adunk 2 évre). Átalakításával, hogy mértéke a 100% – ot, akkor csak meg kell gondolni, hogy az idő komponens:

Ösztönösen, $e^x$ azt jelenti, hogy:

• Mennyi növekedés jutok után x egységnyi idő (100% – os folyamatos növekedési)
• például: 3 után időszakok dollár van e^3$ = 20.08 szer annyi a “cucc”.

$e^x$ egy méretezési tényező, amely megmutatja nekünk, hogy mennyi növekedést kapunk $ x$ időegység után.

A természetes napló az időről szól

a természetes napló A $E^x$ inverze, az ellentétes divatos kifejezés. Apropó képzelet, a Latin neve logaritmus naturali, így a rövidítés ln.

most mit jelent ez az inverz vagy ellentétes dolog?

• $e^x$ lehetővé teszi számunkra, hogy időben csatlakozzunk, és növekedjünk.
• $ \ ln (x)$ lehetővé teszi számunkra, hogy plug in growth and get the time it would take.

például:

• $ e^3$ 20.08. 3 egységnyi idő után 20-zal végzünk.08-szor annyi, mint amivel kezdtük.
• $ \ ln (20.08)$ körülbelül 3. Ha 20.08-as növekedést akarunk, akkor 3 egységet várnánk (ismét 100% – os folyamatos növekedési rátát feltételezve).

velem? A természetes napló megadja nekünk a kívánt növekedés eléréséhez szükséges időt.

logaritmikus aritmetika nem normális

korábban már tanulmányozta a naplókat, és furcsa állatok voltak. Hogyan váltották össze a szorzást? Felosztás kivonásra? Lássuk csak.

mi az a $\ln(1)$? Intuitív módon a kérdés: mennyi ideig várom, hogy 1x-et kapjak a jelenlegi összegemre?

nulla. Zip. Nada. Te már 1x a jelenlegi összeg! Nem kell sok idő 1-ről 1-re nőni.

• $ \ ln (1) = 0$

Ok, mit szólnál egy frakcionált értékhez? Mennyi ideig kap 1/2 a jelenlegi összeg? Feltételezve, hogy folyamatosan növekszik 100% – on, tudjuk, hogy a $\ln(2)$ a Duplázás ideje. Ha megfordítjuk (azaz a negatív időt vesszük figyelembe), akkor a jelenlegi értékünk fele lenne.

• $ \ ln(.5) = – \ ln (2)= -.693$

van értelme, ugye? Ha visszafelé megyünk .693 egység (negatív másodperc, mondjuk) a jelenlegi összeg fele lenne. Általában, akkor flip a frakció, hogy a negatív: $\ln(1/3) = – \ln(3) = -1,09$. Ez azt jelenti, hogy ha visszamegyünk 1.09-es időegységbe, akkor harmada lesz annak, ami most van.

Ok, mi a helyzet a negatív szám természetes naplójával? Mennyi időt vesz igénybe a baktériumok kolóniájának “növekedése” 1 – ről -3-ra?

Ez lehetetlen! Nem lehet “negatív” mennyiségű baktérium, ugye? Legfeljebb (ööö… legalább) lehet nulla, de nincs mód arra, hogy negatív összeget kapjunk a kis fickóktól. A negatív baktériumoknak egyszerűen nincs értelme.

• $ \ ln (\text{negative number}) = \ text{undefined}$

Undefined csak azt jelenti, hogy “nincs idő várni”, hogy negatív összeget kapjon. (Nos, ha képzeletbeli exponenciálokat használunk, van megoldás. De ma tartsuk valósnak.)

logaritmikus szorzás Mighty Fun

mennyi ideig tart, hogy növekszik 9x a jelenlegi összeg? Persze, használhatnánk az ln-t (9). De ez túl könnyű, legyünk mások.

a 9x növekedést háromszorosának tekinthetjük ($\ln(3)$ időegység), majd újra megháromszorozhatjuk (újabb $\ln(3)$ időegység):

• ideje növekedni 9x = $ \ ln (9)$ = ideje újra megháromszorozódni = $ \ ln (3) + \ ln(3)$

érdekes. Bármely növekedési szám, mint 20, 2x növekedésnek tekinthető, amelyet 10x növekedés követ. Vagy 4x növekedés, amelyet 5x növekedés követ. Vagy 3x növekedés, amelyet 6, 666 x növekedés követ. Látod a mintát?

• $ \ ln(a*b) = \ln(a) + \ln(b)$

a Times B = log(a) + log (b) naplója. Ennek a kapcsolatnak akkor van értelme, ha úgy gondolja, hogy ideje növekedni.

Ha növekedni akarunk 30x várhatunk $\ln(30)$ egyszerre, vagy egyszerűen csak várj $\ln(3)$, a hármas, akkor várj $\ln(10)$, nő 10x újra. A nettó hatás ugyanaz, tehát a nettó időnek is azonosnak kell lennie (és az is).

mi a helyzet a divízióval? $ \ ln (5/3)$ azt jelenti: mennyi ideig tart 5-ször növekedni, majd 1/3-ot venni?

Nos, az 5-ször növekvő $ \ ln(5)$. A növekvő 1/3 $ – \ ln (3)$ időegység. Tehát

• $ \ ln(5/3) = \ ln (5) – \ ln(3)$

ami azt mondja: nő 5-ször, és “menj vissza az időben”, amíg van egy harmadik, hogy az összeg, így te marad 5/3 növekedés. Általában van

• $\ln(a/b) = \ ln (a)- \ ln (b)$

remélem, hogy a logaritmus furcsa matematikája értelmet nyer: a növekedés sokszorosítása az idő hozzáadásával válik, a növekedés felosztása az idő kivonásává válik. Ne jegyezd meg a szabályokat, értsd meg őket.

természetes naplók használata bármilyen sebességgel

“biztos,” azt mondod, ” Ez a napló cucc 100% – os növekedéshez működik, de mi a helyzet az 5% – kal, amelyet általában kapok?”

Ez nem probléma. Az” idő”, amit a $\ln ()$ – ból kapunk vissza, valójában az árfolyam és az idő kombinációja, az” x ” A $E^x$ egyenletünkből. Csak 100% – ot feltételezünk, hogy egyszerű legyen, de más számokat is használhatunk.

tegyük fel, hogy 30x növekedést akarunk: csatlakoztassuk a $\ln(30)$ – t és kapjuk meg a 3.4-et. Ez azt jelenti:

• $e^x = \ text{growth}$
• $e^{3.4} = 30$

és intuitív módon ez az egyenlet azt jelenti, hogy”100% – os hozam 3,4 évig 30x növekedés”. Vegyük úgy, hogy az egyenlet, hogy:

Tudjuk módosítani “arány”, illetve az “idő”, amíg ráta * idő = 3.4. Tegyük fel például, hogy 30x növekedést akarunk-mennyi ideig várunk 5% – os megtérülést feltételezve?

• $ \ ln (30) = 3,4$
• $\text{rate} * \text{time} = 3.4$
• $.05 * \ text{time} = 3.4$
• $\text{time} = 3.4/.05 = 68 \ text{years}$

intuitív módon azt gondolom, hogy ” $ \ ln (30) = 3,4$, tehát 100% – os növekedésnél 3,4 évig tart. Ha megduplázom a növekedés ütemét, felére csökkentem a szükséges időt.”

• 100% 3.4 év = 1.0 * 3.4 = 3.4
• 200% – os 1.7 év = 2.0 * 1.7 = 3.4
• 50% 6.8 év = 0.5 * 6.8 = 3.4
• 5% 68 év = .05 * 68 = 3,4

Cool, eh? A természetes napló használható bármilyen kamatláb vagy idő, amíg a termék ugyanaz. Mozgassa a változókat, amennyit csak akar.

félelmetes példa: a szabály 72

a szabály 72 egy mentális matematikai parancsikon megbecsülni a szükséges időt, hogy megduplázza a pénzt. Ki fogjuk deríteni (hurrá!) és még jobb, hogy intuitív módon fogjuk megérteni.

mennyi ideig tart, hogy megduplázza a pénzt 100% – os kamat, össze minden évben?

Uh oh. Folyamatosan használjuk a természetes naplót, de most éves kamatot kér? Ez nem fogja elrontani a formulánkat? Igen, így lesz, de elfogadható kamatok mellett, mint 5%, 6% vagy akár 15%, nincs sok különbség az éves kamatok és a teljes folyamatos kamatok között. Tehát a durva képlet nagyjából működik, és úgy teszünk,mintha folyamatosan érdeklődnénk.

most a kérdés egyszerű: mennyi ideig kell duplázni 100% – os kamat mellett? ln (2) = .693. Kell hozzá .693 egységnyi idő (év, ebben az esetben), hogy megduplázza a pénzt folyamatos összetételű, amelynek mértéke 100%.

ok, mi van, ha a kamat nem 100% Mi van, ha 5% vagy 10%?

egyszerű. Mindaddig, amíg az arány * idő = .693, megduplázzuk a pénzünket:

• rate * time = .693
• idő = .693 / rate

tehát, ha csak 10% – os növekedésünk lenne, akkor megteszi .693 / .10 vagy 6, 93 év a dupláig.

a dolgok egyszerűsítése érdekében szorozzuk meg 100-mal, így inkább 10-ről beszélhetünk .10:

• idő dupla = 69.3 / Arány, ahol Arány feltételezzük, hogy százalékban.

most az 5% – os növekedés megduplázódásának ideje 69, 3 / 5 vagy 13, 86 év. A 69.3 azonban nem a leginkább osztható szám. Válasszunk egy közeli szomszédot, a 72-et, ami 2, 3, 4, 6, 8-mal és még sok más számmal osztható.

• idő dupla = 72/Arány

ami a szabály 72! Könnyű szellő.

Ha meg szeretné találni az időt, hogy hármas, akkor használja ln(3) ~ 109.8 és kap

• ideje tripla = 110 / rate

ami egy másik hasznos ökölszabály. A 72-es szabály a kamatok, a népességnövekedés, a baktériumkultúrák és bármi, ami exponenciálisan növekszik.

hol innen?

remélem, hogy a természetes naplónak több értelme van — megmondja az exponenciális növekedéshez szükséges időt. Úgy vélem, hogy “természetes”, mert e az egyetemes növekedési ütem, így ln lehet tekinteni az” univerzális ” módja annak, hogy kitaláljuk, mennyi ideig tart a dolgok növekedni.

amikor $\ln(x)$ – t lát, Gondoljon csak arra, hogy “mennyi idő alatt növekszik x-re”. A következő cikkben összehozzuk e-t és ln-t, és a matek édes aromája megtölti a levegőt.

Függelék: Az E

Gyors kvíz természetes naplója: mi az a $ \ ln (e)$?

• a matematikai robot azt mondja: mivel ezeket inverz függvényeknek definiálják, egyértelműen $\ln(E) = 1$
• Az intuitív ember: ln (e) az az idő, amely az “e” növekedési egységek megszerzéséhez szükséges (körülbelül 2.718). De e az összeg a növekedés után 1 egységnyi idő, így $ \ ln(E) = 1$.

gondolkodj intuitív módon.

Egyéb Hozzászólásaidat Ebben A Sorozatban

1. Egy Intuitív Útmutató Exponenciális Függvények a & e
2. Demystifying a Természetes Logaritmusát (ln)
3. Vizuális Útmutató Egyszerű, Összetett, Folyamatos Kamatok
4. Közös meghatározása e (Színezett)
5. Megértését Is (Miért nem 0^0 = 1?)
6. logaritmusok használata a Való Világban
7. hogyan gondolkodjunk Exponensekkel és Logaritmusokkal
8. diszkrét vs. folyamatos növekedés megértése
9. mit jelent valójában egy exponens?
10. K: Miért különleges az e? (2.718…, nem 2, 3.7 vagy más szám?)