Atomic Orbitals
az orbital a Bohr pályájának kvantummechanikai finomítása. Ellentétben egy egyszerű, kör alakú, rögzített sugarú pályával, a pályák matematikailag származtatott térrészek, amelyek különböző valószínűségekkel rendelkeznek elektronnal.
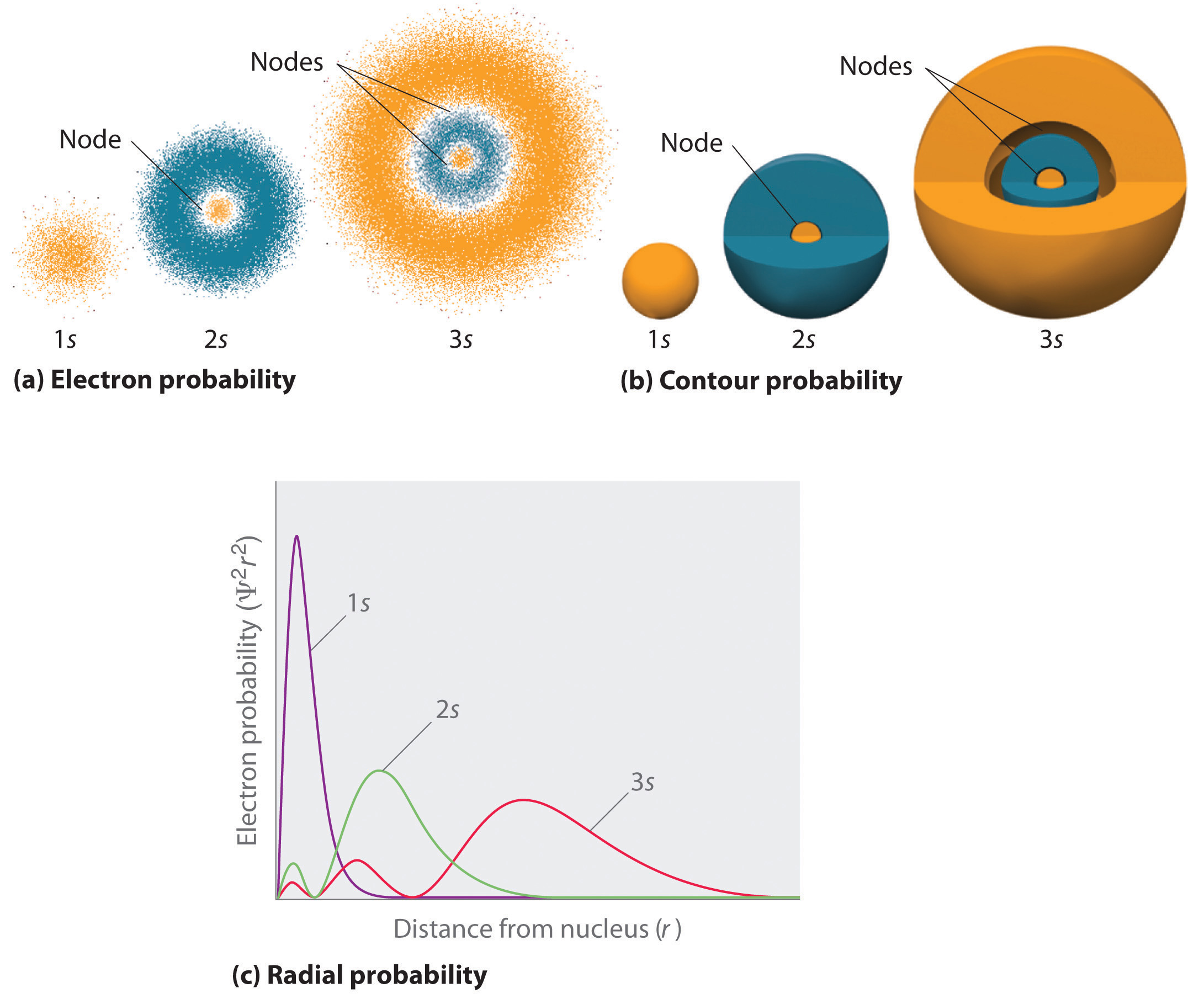
az elektron valószínűségi eloszlások ábrázolásának egyik módját a 6.5.2 ábra szemlélteti a hidrogén 1s orbitális pályájára. Mivel a Ψ2 megadja annak valószínűségét, hogy egy adott térben (például egy köbös pikométerben) elektront talál, a Ψ2 telken a magtól (r) való távolság a valószínűségi sűrűség diagramja. Az 1s orbitális gömbszimmetrikus, így az 1s elektron megtalálásának valószínűsége egy adott ponton csak a magtól való távolságától függ. A valószínűségi sűrűség a legnagyobb r = 0-nál (a magnál), és folyamatosan csökken a távolság növekedésével. Az r nagyon nagy értékeinél az elektron valószínűségi sűrűsége nagyon kicsi, de nem nulla.
ezzel szemben kiszámolhatjuk a radiális valószínűséget (annak valószínűségét, hogy egy 1S elektronot r távolságra találunk a magtól), az R1, r2, r3,…, rx − 1, rx sugár x gömbhéj sorozatának minden pontján lévő elektron valószínűségeinek összeadásával. Valójában az atomot nagyon vékony koncentrikus héjakra osztjuk, hasonlóan a hagyma rétegeihez (a) A \(\PageIndex{1}\) ábrán), és kiszámítjuk az elektron megtalálásának valószínűségét minden gömbhéjon. Emlékezzünk vissza, hogy az elektron valószínűségi sűrűsége a legnagyobb r = 0-nál (B rész) a \(\PageIndex{1}\) ábrán), így a pontok sűrűsége a legnagyobb a legkisebb gömbhéjak esetében a \(\PageIndex{1}\) ábrán. Ezzel szemben az egyes gömbhéjak felülete egyenlő a 4nr2-vel, ami nagyon gyorsan növekszik a \(\PageIndex{1}\) ábrán látható R (C rész) növekedésével. Mivel a gömbhéjak felülete gyorsabban növekszik az R növekedésével, mint az elektron valószínűségi sűrűsége csökken, a radiális valószínűség plotja egy adott távolságban (D rész) a \(\PageIndex{1}\) ábrán). A legfontosabb, ha r nagyon kicsi, a gömb alakú héj felülete olyan kicsi, hogy a maghoz közeli elektron megtalálásának teljes valószínűsége nagyon alacsony; a magban az elektron valószínűsége eltűnik (D rész) A \ábrán (\PageIndex{1}\)).

a hidrogénatom esetében a radiális valószínűségi telek csúcsa r = 0,529 Å (52,9 pm), amely pontosan a Bohr által az n = 1 pályára számított sugár. Így a kvantummechanikából nyert legvalószínűbb sugár megegyezik a klasszikus mechanika által kiszámított sugárral. Bohr modelljében azonban az elektront az idő 100% – ában feltételezték, míg a kvantummechanikai Schrödinger modellben ez a távolság csak egy része. A két modell közötti különbség az elektron hullámszerű viselkedésének és a Heisenberg bizonytalansági elvnek tulajdonítható.
ábra \ (\PageIndex{2}\) összehasonlítja a hidrogén 1s, 2s és 3s pályáinak elektron valószínűségi sűrűségét. Ne feledje, hogy mind a három szferikusan szimmetrikus. A 2s és 3s orbitáloknál azonban (és minden más s orbitálnál is) az elektron valószínűségi sűrűsége nem esik le simán a növekvő r-vel. ehelyett a radiális valószínűségi parcellákban (C rész) a \(\PageIndex{2}\) ábrán minimumok és maximák sorozata figyelhető meg. A minimumok gömb alakú csomópontoknak felelnek meg (nulla elektron valószínűségű régiók), amelyek váltakoznak a nem nulla elektron valószínűségű gömb alakú régiókkal.