- lärandemål
- arbete mot gravitation
- omvandling mellan potentiell energi och kinetisk energi
- använda potentiell energi för att förenkla beräkningarna
- exempel 1. Kraften att sluta falla
- strategi
- lösning
- diskussion
- exempel 2. Att hitta hastigheten på en berg-och dalbana från dess höjd
- strategi
- lösning för del 1
- lösning för del 2
- diskussion och implikationer
- göra anslutningar: ta hem-undersökning—konvertera Potential till kinetisk energi
- avsnitt sammanfattning
- konceptuella frågor
- problem& övningar
- ordlista
- valda lösningar på problem & övningar
lärandemål
i slutet av detta avsnitt kommer du att kunna:
- förklara gravitationspotential energi när det gäller arbete mot gravitation.
- visa att gravitationspotentialenergin hos ett objekt med massa m vid höjd h på jorden ges av PEg = mgh.
- visa hur kunskap om potentiell energi som funktion av position kan användas för att förenkla beräkningar och förklara fysiska fenomen.
arbete mot gravitation
att klättra trappor och lyfta föremål är arbete i både vetenskaplig och vardaglig mening—det är arbete mot gravitationskraften. När det finns arbete sker en omvandling av energi. Arbetet mot gravitationskraften går in i en viktig form av lagrad energi som vi kommer att utforska i detta avsnitt.

Figur 1. (a) arbetet med att lyfta vikten lagras i massjordsystemet som gravitationspotentialenergi. (b) när vikten rör sig nedåt överförs denna gravitationspotentialenergi till gökklockan.
låt oss beräkna det arbete som utförts för att lyfta ett objekt med massa m genom en höjd h, såsom i Figur 1. Om objektet lyfts rakt upp med konstant hastighet, är den kraft som behövs för att lyfta den lika med dess vikt mg. Arbetet på massan är då W = Fd = mgh. Vi definierar detta för att vara gravitationspotentialenergin (PEg) som sätts in i (eller vunnits av) objektjordsystemet. Denna energi är förknippad med separationstillståndet mellan två objekt som lockar varandra genom gravitationskraften. För enkelhets skyld hänvisar vi till detta som pinnen som uppnås av objektet och erkänner att detta är energi lagrad i jordens gravitationsfält. Varför använder vi ordet ”system”? Potentiell energi är en egenskap hos ett system snarare än ett enda objekt—på grund av dess fysiska position. Ett objekts gravitationspotential beror på dess position i förhållande till omgivningen inom Jordobjektsystemet. Kraften som appliceras på objektet är en yttre kraft, från utsidan av systemet. När det gör positivt arbete ökar det gravitationspotentialenergin i systemet. Eftersom gravitationspotentialenergi beror på relativ position behöver vi en referensnivå för att ställa in den potentiella energin lika med 0. Vi väljer vanligtvis denna punkt för att vara jordens yta, men denna punkt är godtycklig; det som är viktigt är skillnaden i gravitationspotentialenergi, eftersom denna skillnad är vad som hänför sig till det arbete som utförts. Skillnaden i gravitationspotentialenergi hos ett objekt (i Jordobjektsystemet) mellan två stegpinnar i en stege kommer att vara densamma för de två första stegpinnarna som för de två sista stegpinnarna.
omvandling mellan potentiell energi och kinetisk energi
gravitationspotential energi kan omvandlas till andra former av energi, såsom kinetisk energi. Om vi släpper massan kommer gravitationskraften att göra en mängd arbete som är lika med mgh på den, vilket ökar dess kinetiska energi med samma mängd (genom arbetsenergisatsen). Vi kommer att finna det mer användbart att bara överväga omvandlingen av PEg till KE utan att uttryckligen överväga mellansteget i arbetet. (Se Exempel 2.) Denna genväg gör det lättare att lösa problem med energi (om möjligt) snarare än att uttryckligen använda krafter.
närmare bestämt definierar vi förändringen i gravitationspotentialenergi som att vara Jacobpeg = mgh, där vi för enkelhetens skull betecknar höjdförändringen med h snarare än den vanliga Jacobh. Observera att h är positivt när den slutliga höjden är större än den ursprungliga höjden och vice versa. Till exempel, om en 0,500 kg massa hängde från en gökur höjs 1.00 m, då är dess förändring i gravitationspotentialenergi
\begin{array}{lll}mgh&&(0.500\text{ kg})(9.80\text{ m/s}^2)(1.00\text{ m})\\\text{ }&&4.90\text{ kg}\cdot\text{m}^2\Text{/s}^2=4.90\text{ j}\end{array}\\
Observera att enheterna för gravitationspotentialenergi visar sig vara joule, samma som för arbete och andra former av energi. När klockan går sänks massan. Vi kan tänka på massan som gradvis ger upp sin 4.90 J gravitationspotentialenergi, utan att direkt överväga tyngdkraften som gör arbetet.
använda potentiell energi för att förenkla beräkningarna

Figur 2. Förändringen i gravitationspotentialenergi (Kubpeg) mellan punkterna A och B är oberoende av vägen.
ekvationen Jacobpeg = mgh gäller för alla vägar som har en höjdförändring på h, inte bara när massan lyfts rakt upp. (Se Figur 2.) Det är mycket lättare att beräkna mgh (en enkel multiplikation) än att beräkna det arbete som utförts längs en komplicerad väg. Tanken med gravitationspotentialenergi har den dubbla fördelen att den är mycket allmänt tillämplig och det gör beräkningarna enklare.
Från och med nu kommer vi att överväga att varje förändring i vertikal position h av en massa m åtföljs av en förändring i gravitationspotential energi mgh, och vi kommer att undvika motsvarande men svårare uppgift att beräkna arbete som utförs av eller mot gravitationskraften.
Acigpeg = mgh för vilken väg som helst mellan de två punkterna. Gravity är en av en liten klass av krafter där arbetet som utförs av eller mot kraften bara beror på Start-och slutpunkterna, inte på vägen mellan dem.
exempel 1. Kraften att sluta falla
a 60.0 kg person hoppar på golvet från en höjd av 3,00 m. om han landar styvt (med knälederna komprimerade med 0,500 cm), beräkna kraften på knäleden.
strategi
denna persons energi bringas till noll i denna situation av det arbete som utförs på honom vid golvet när han stannar. Den ursprungliga pinnen omvandlas till KE när han faller. Golvets arbete minskar denna kinetiska energi till noll.
lösning
det arbete som utförs på personen vid golvet när han stannar ges av W = Fd cos michai = – Fd, med ett minustecken eftersom förskjutningen under stopp och kraften från golvet är i motsatta riktningar (cos michai = cos 180 michai = -1). Golvet tar bort energi från systemet, så det gör negativt arbete.
den kinetiska energi som personen har när han når golvet är mängden potentiell energi som förloras genom att falla genom höjden h: KE = −Jacobpeg = −mgh.
avståndet d som personens knän böjer är mycket mindre än höjden h på hösten, så den ytterligare förändringen i gravitationspotentialenergi under knäböjningen ignoreras.
arbetet som utförs av golvet på personen stoppar personen och ger personens kinetiska energi till noll: W = −KE = mgh.
kombinera denna ekvation med uttrycket för W ger −Fd = mgh.
erinrar om att h är negativt eftersom personen föll ner, ges kraften på knäleden av
\displaystyle{F}=-\frac{mgh}{d}=-\frac{\left(60.0\text{ kg}\right)\left(9.80\text{ m/s}^2\right)\left(-3.00\text{ m}\right)}{5.00\times10^{-3}\text{ m}}=3.53\times10^5\text{ N}\\
diskussion
en sådan stor kraft (500 gånger mer än personens vikt) över den korta slagtiden räcker för att bryt ben. Ett mycket bättre sätt att dämpa chocken är att böja benen eller rulla på marken, vilket ökar tiden över vilken kraften verkar. En böjningsrörelse på 0,5 m på detta sätt ger en kraft 100 gånger mindre än i exemplet. En känguruhoppning visar denna metod i aktion. Känguru är det enda stora djuret som använder hopping för rörelse, men chocken i hopping dämpas av böjningen av bakbenen i varje hopp. (Se Figur 3.)

Figur 3. Arbetet som utförs av marken på känguru minskar sin kinetiska energi till noll när den landar. Genom att applicera markens kraft på bakbenen över ett längre avstånd reduceras påverkan på benen. (kredit: Chris Samuel, Flickr)
exempel 2. Att hitta hastigheten på en berg-och dalbana från dess höjd
- vad är den slutliga hastigheten på berg-och dalbanan som visas i Figur 4 om den börjar från Vila högst upp på 20,0 m-kullen och arbete som utförs av friktionskrafter är försumbar?
- Vad är dess sluthastighet (återigen antar försumbar friktion) om dess initialhastighet är 5,00 m/s?
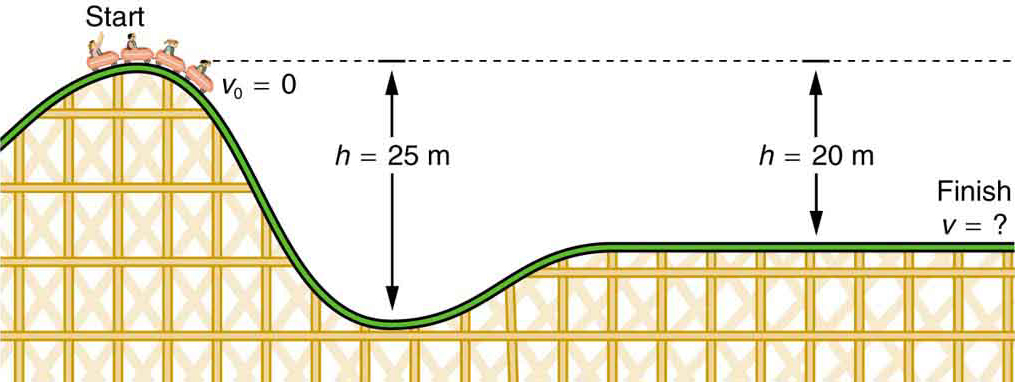
Figur 4. Hastigheten på en berg-och dalbana ökar när tyngdkraften drar den nedförsbacke och är störst vid sin lägsta punkt. Sett i termer av energi omvandlas berg-och dalbana-Jordsystemets gravitationspotentialenergi till kinetisk energi. Om arbete som utförs av friktion är försumbar, omvandlas alla Jacobeg till KE.
strategi
berg-och dalbanan förlorar potentiell energi när den går nedförsbacke. Vi försummar friktion, så att den återstående kraften som utövas av spåret är den normala kraften, som är vinkelrätt mot rörelseriktningen och inte fungerar. Nettoarbetet på berg-och dalbanan görs sedan av gravitationen ensam. Förlusten av gravitationspotential energi från att röra sig nedåt genom ett avstånd h är lika med vinsten i kinetisk energi. Detta kan skrivas i ekvationsform som-Ubigpeg = UBIGKE. Med hjälp av ekvationerna för PEg och KE kan vi lösa för sluthastigheten v, vilket är den önskade kvantiteten.
lösning för del 1
här är den initiala kinetiska energin noll, så att \Delta \ text{KE}=\frac{1}{2}mv^2\\. Ekvationen för förändring i potentiell energi säger att Bisexuell = mgh. Eftersom h är negativt i det här fallet kommer vi att skriva om detta som Jacobpeg = −mg|h| för att visa minustecknet tydligt. Således blir-Ubicpeg = UBICKE mg / h/= \ frac{1}{2}{mv}^2\\.
lösa för v, finner vi att massan avbryts och att v=\sqrt{2G|h|}\\.
ersätta kända värden,
\begin{array}{lll}v&&\sqrt{2\left(9.80\text{ m/s}^2\right)\left(20.0\text{ m}\right)}\\\text{ }&&19.8\text{ m/s}\end{array}\\
lösning för del 2
igen −sacribpeg = sacribke. I detta fall finns det initial kinetisk energi, så
\Delta\text{KE}=\frac{1}{2}mv^2-\frac{1}{2}mv_0^2\\.
således mg / h/ = \frac{1}{2}MV^2-\frac{1}{2}mv_0^2\\.
omarrangering ger \frac{1}{2}MV^2=mg|h|+\frac{1}{2}mv+0^2\\.
detta innebär att den slutliga kinetiska energin är summan av den initiala kinetiska energin och gravitationspotentialenergin. Massan avbryts igen och v=\sqrt{2G|h / +v_0^2}\\.
denna ekvation är mycket lik kinematiksekvationen v=\sqrt{v_0^2 + 2AD}\\, men det är mer allmänt—kinematiksekvationen är endast giltig för konstant acceleration, medan vår ekvation ovan är giltig för vilken väg som helst oavsett om objektet rör sig med en konstant acceleration. Nu ersätter kända värden
\begin{array}{lll}v&&\sqrt{2\left(9.80\text{ m/s}^2\right)\left(20.0\text{ m}\höger)+\vänster(5.00\text{ m/s}\höger)^2}\\\text{ }&&20.4 \ text{ m / s} \ end{array}\ \
diskussion och implikationer
Observera först att massan avbryts. Detta överensstämmer helt med observationer gjorda i fallande föremål att alla föremål faller i samma takt om friktionen är försumbar. För det andra beaktas endast berg-och dalbanans hastighet, det finns ingen information om dess riktning när som helst. Detta avslöjar en annan allmän sanning. När friktionen är försumbar beror hastigheten på en fallande kropp endast på dess initialhastighet och höjd, och inte på dess massa eller den väg som tagits. Till exempel kommer berg-och dalbanan att ha samma sluthastighet oavsett om den faller 20,0 m rakt ner eller tar en mer komplicerad väg som den i figuren. För det tredje, och kanske oväntat, är sluthastigheten i del 2 större än i del 1, men betydligt mindre än 5, 00 m/s. Slutligen notera att hastigheten kan hittas i vilken höjd som helst längs vägen genom att helt enkelt använda lämpligt värde på h vid intressepunkten.
Vi har sett att arbete som utförs av eller mot gravitationskraften bara beror på Start-och slutpunkterna, och inte på vägen mellan, så att vi kan definiera det förenklande begreppet gravitationspotential energi. Vi kan göra samma sak för några andra krafter, och vi kommer att se att detta leder till en formell definition av lagen om bevarande av energi.
göra anslutningar: ta hem-undersökning—konvertera Potential till kinetisk energi
man kan studera omvandlingen av gravitationspotentialenergi till kinetisk energi i detta experiment. På en jämn, jämn yta, använd en linjal av det slag som har ett spår som löper längs dess längd och en bok för att göra en lutning (se Figur 5). Placera en marmor i 10 cm-positionen på linjalen och låt den rulla ner linjalen. När den träffar den plana ytan mäter du den tid det tar att rulla en meter. Placera nu marmorn på 20 cm och 30 cm positioner och mät igen de tider det tar att rulla 1 m på den plana ytan. Hitta marmorens hastighet på den plana ytan för alla tre positionerna. Plothastighet kvadrerad mot det avstånd som marmorn reste. Vad är formen på varje tomt? Om formen är en rak linje visar diagrammet att marmorens kinetiska energi i botten är proportionell mot dess potentiella energi vid frigöringspunkten.

Figur 5. En marmor rullar ner en linjal, och dess hastighet på den plana ytan mäts.
avsnitt sammanfattning
- arbete som utförs mot tyngdkraften vid lyftning av ett objekt blir potentiell energi i objektjordsystemet.
- förändringen i gravitationspotentialenergin, Ubicpeg, är Ubicpeg = mgh, med h är ökningen i höjd och g accelerationen på grund av tyngdkraften.
- gravitationspotentialenergin hos ett objekt nära jordens yta beror på dess position i massjordsystemet. Endast skillnader i gravitationspotentialenergi, Bisexuell, har fysisk betydelse.
- som ett objekt faller ner utan friktion förändras dess gravitationspotentialenergi till kinetisk energi som motsvarar ökande hastighet, så att JACOBKE = −Jacobpeg
konceptuella frågor
- I exempel 2 beräknade vi sluthastigheten för en berg-och dalbana som sjönk 20 m i höjd och hade en initialhastighet på 5 m / s nedförsbacke. Anta att berg-och dalbanan hade haft en initialhastighet på 5 m/s uppförsbacke istället, och den sträckte sig uppåt, stannade och rullade sedan tillbaka ner till en sista punkt 20 m under starten. Vi skulle i så fall finna att den hade samma slutliga hastighet. Förklara när det gäller bevarande av energi.
- beror det arbete du gör på en bok när du lyfter den på en hylla på vägen? På den tid det tar? På höjden av hyllan? På bokens massa?
problem& övningar
- en vattenkraftanläggning (se Figur 6) omvandlar gravitationspotentialenergin av vatten bakom en damm till elektrisk energi. (A) Vad är gravitationspotentialenergin i förhållande till generatorerna i en sjö med volym 50.0 km3 (massa = 5,00 1013 kg 1013 kg), med tanke på att sjön har en genomsnittlig höjd på 40,0 m över generatorerna? (B) jämför detta med den energi som lagras i en 9-megaton fusionsbomb.

Figur 6. Vattenkraftanläggning(kredit: Denis Belevich, Wikimedia Commons)
- (a) hur mycket gravitationspotentialenergi (i förhållande till marken på vilken den är byggd) lagras i Cheops stora Pyramid, med tanke på att dess massa är ca 7 kg 109 kg och dess masscentrum är 36.5 m över den omgivande marken? (b) Hur jämför denna energi med en persons dagliga matintag?
- Antag att en 350-g kookaburra (en stor Kungsfiskare) plockar upp en 75-g orm och höjer den 2,5 m från marken till en gren. (a) Hur mycket arbete gjorde fågeln på ormen? (B) Hur mycket arbete gjorde den för att höja sitt eget masscentrum till grenen?
- I exempel 2 fann vi att hastigheten på en berg-och dalbana som hade sjunkit 20,0 m bara var något större när den hade en initialhastighet på 5,00 m/s än när den började från Vila. Detta innebär att JACOBPE >> KEi. Bekräfta detta uttalande genom att ta förhållandet mellan XIAPE och KEi. (Observera att massan avbryts.)
- en 100-g leksaksbil drivs av en komprimerad fjäder som startar den i rörelse. Bilen följer den böjda banan i Figur 7. Visa att leksaksbilens sluthastighet är 0,687 m/s om dess initialhastighet är 2,00 m / s och den kustar upp den friktionsfria sluttningen och får 0,180 m i höjd.

Figur 7. En leksaksbil flyttar upp en sluttande bana. (kredit: Leszek Leszczynski, Flickr)
- i en utförsåkning, överraskande, liten fördel uppnås genom att få en löpande start. (Detta beror på att den initiala kinetiska energin är liten jämfört med vinsten i gravitationspotentialenergi på även små kullar.) För att visa detta, hitta den slutliga hastigheten och den tid det tar för en skidåkare som skies 70,0 m längs en 30 ml sluttning försummar friktion: (A) från Vila. (b) börjar med en initialhastighet på 2,50 m/s. (c) överraskar svaret dig? Diskutera varför det fortfarande är fördelaktigt att få en löpande start i mycket konkurrenskraftiga evenemang.
ordlista
gravitationspotential energi: den energi ett objekt har på grund av sin position i ett gravitationsfält
valda lösningar på problem & övningar
1. a) 1,96 1016 J. B) förhållandet mellan gravitationspotentialenergi i sjön och den energi som lagras i bomben är 0,52. Det vill säga den energi som lagras i sjön är ungefär hälften så stor som i en fusionsbomb på 9 megaton.
3. a) 1,8 J; b) 8,6 J
5. {v} _ {f}= \ sqrt{2gh + {v_0}^2}=\sqrt{2 \ vänster (9.80\text{ m / s}^2\höger) \ vänster (-0.180\text{ m} \ höger)+ \ vänster (2.00\text{ m / s} \ höger)^2} = 0.687\text{ m / s}\\