Quelques choses intéressantes sur les angles et les cercles.
- Angle inscrit
- Théorèmes d’angle inscrit
- Exemple: Quelle est la taille de l’angle POQ? (O est le centre du cercle)
- Exemple : Quelle est la taille de l’angle CBX ?
- Angle dans un demi-cercle (Théorème de Thalès)
- Une autre Bonne raison Pour laquelle Cela fonctionne
- Exemple: Quelle est la taille de l’angle BAC?
- Trouver le Centre d’un cercle
- Quadrilatère cyclique
- Exemple: Quelle est la taille de l’angle WXY?
Angle inscrit
Tout d’abord, une définition:
Angle inscrit: un angle fait à partir de points situés sur la circonférence du cercle.
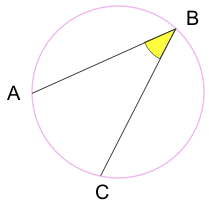
A et C sont des « points finaux »
B est le « point d’apex »
Jouez avec ici:
Lorsque vous déplacez le point « B », qu’arrive-t-il à l’angle?
Théorèmes d’angle inscrit
Un angle inscrit a° est la moitié de l’angle central 2a°
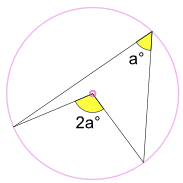
(Appelé Théorème de l’angle au Centre)
Et (en gardant les points finaux fixes)…
… l’angle a° est toujours le même,
peu importe où il se trouve sur le même arc entre les points d’extrémité:
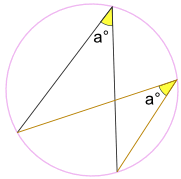
L’angle a° est le même.
(Appelé les Angles Sous-tendus par le Même Théorème d’Arc)
Exemple: Quelle est la taille de l’angle POQ? (O est le centre du cercle)
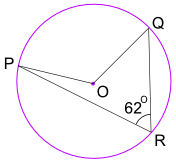
Angle POQ= 2 × Angle PRQ = 2 × 62° = 124°
Exemple : Quelle est la taille de l’angle CBX ?
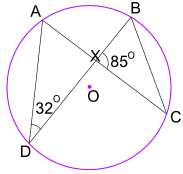
L’angle ADB=32° est également égal à l’angle ACB.
Et l’angle ACB est également égal à l’angle XCB.
Donc, dans le triangle BXC, nous connaissons l’angle BXC = 85 ° et l’angle XCB = 32 °
Utilisez maintenant les angles d’un triangle ajoutés à 180 ° :
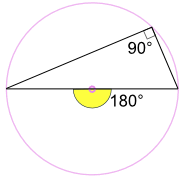
Angle dans un demi-cercle (Théorème de Thalès)
Un angle inscrit sur le diamètre d’un cercle est toujours un angle droit:
(Les points d’extrémité sont l’une ou l’autre des extrémités du diamètre d’un cercle,
le point apex peut être n’importe où sur circonférence.)
|
Pourquoi? Parce: L’angle inscrit 90 ° est la moitié de l’angle central 180 ° (En utilisant « Théorème de l’angle au centre » ci-dessus) |
 |
Une autre Bonne raison Pour laquelle Cela fonctionne
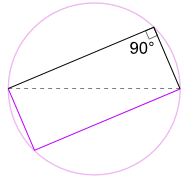
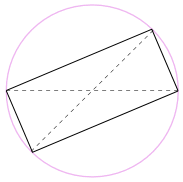
Nous pourrions également faire pivoter la forme autour 180° pour faire un rectangle !
C’est un rectangle, car tous les côtés sont parallèles et les deux diagonales sont égales.
Et donc ses angles internes sont tous des angles droits (90°).
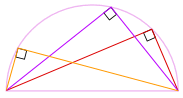
Alors voilà! Peu importe où cet angle est
sur la circonférence, il est toujours de 90 °
Exemple: Quelle est la taille de l’angle BAC?
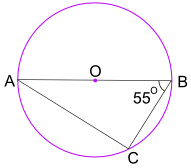
L’Angle dans le théorème du demi-cercle nous indique que l’Angle ACB = 90 °
Utilisez maintenant les angles d’un triangle add à 180 ° pour trouver l’Angle BAC:
Trouver le Centre d’un cercle
Nous pouvons utiliser cette idée pour trouver le centre d’un cercle:
- dessinez un angle droit de n’importe où sur la circonférence du cercle, puis dessinez le diamètre où les deux jambes frappent le cercle
- recommence mais pour un diamètre différent
Où les diamètres se croisent est le centre!
Quadrilatère cyclique
|
Un Quadrilatère « Cyclique » a chaque sommet sur la circonférence d’un cercle: |
 |
|
Un quadrilatère cyclique |
|
|
Un quadrilatère cyclique |
|
|
Un quadrilatère cyclique |
|
|
Les angles opposés du quadrilatère s’ajoutent à 180° :
|
 |
Exemple: Quelle est la taille de l’angle WXY?
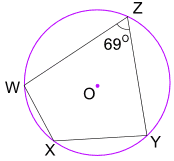
Opposite angles of a cyclic quadrilateral add to 180°

