Objectifs d’apprentissage

À la fin de cette section, vous pourrez:

• Expliquer l’énergie potentielle gravitationnelle en termes de travail effectué contre la gravité.
• Montrer que l’énergie potentielle gravitationnelle d’un objet de masse m à hauteur h sur Terre est donnée par PEg=mgh.
• Montrer comment la connaissance de l’énergie potentielle en fonction de la position peut être utilisée pour simplifier les calculs et expliquer les phénomènes physiques.

Figure 1. (a) Le travail effectué pour soulever le poids est stocké dans le système masse-Terre sous forme d’énergie potentielle gravitationnelle. (b) Au fur et à mesure que le poids descend, cette énergie potentielle gravitationnelle est transférée à la pendule à coucou.

Figure 2. La variation de l’énergie potentielle gravitationnelle (ΔPEg) entre les points A et B est indépendante de la trajectoire.

Exemple 1. La Force pour arrêter de tomber

A 60.une personne de 0 kg saute sur le sol d’une hauteur de 3,00 m. S’il atterrit raide (avec ses articulations du genou se comprimant de 0,500 cm), calculez la force sur les articulations du genou.

Stratégie

L’énergie de cette personne est ramenée à zéro dans cette situation par le travail effectué sur elle par le sol lorsqu’elle s’arrête. La cheville initiale se transforme en KE lorsqu’il tombe. Le travail effectué par le sol réduit cette énergie cinétique à zéro.

Solution

Le travail effectué sur la personne par le sol lorsqu’elle s’arrête est donné par W = Fd cos θ =-Fd, avec un signe moins car le déplacement lors de l’arrêt et la force du sol sont dans des directions opposées (cos θ = cos 180º =-1). Le sol élimine l’énergie du système, il fait donc un travail négatif.

L’énergie cinétique de la personne lorsqu’elle atteint le sol est la quantité d’énergie potentielle perdue en tombant à travers la hauteur h: KE =−ΔPEg =−mgh.

La distance d que les genoux de la personne plient est beaucoup plus petite que la hauteur h de la chute, de sorte que le changement supplémentaire d’énergie potentielle gravitationnelle pendant la courbure du genou est ignoré.

Le travail W effectué par le sol sur la personne arrête la personne et amène l’énergie cinétique de la personne à zéro: W =-KE = mgh.

La combinaison de cette équation avec l’expression de W donne −Fd=mgh.

Rappelant que h est négatif parce que la personne est tombée, la force sur les articulations du genou est donnée par

\displaystyle{F}=-\frac{mgh}{d}=-\frac{\left(60.0\text{kg}\right)\left(9,80\text{m/s}^2\right)\left(-3,00\text{m}\right)}{5,00\times10^{-3}\text{m}} = 3,53\times10^5\text{N}\\

Discussion

Une force aussi importante (500 fois plus que le poids de la personne) sur le court temps d’impact suffit à cassez les os. Une bien meilleure façon d’amortir le choc consiste à plier les jambes ou à rouler sur le sol, ce qui augmente le temps pendant lequel la force agit. Un mouvement de flexion de 0,5 m donne ainsi une force 100 fois plus faible que dans l’exemple. Le saut d’un kangourou montre cette méthode en action. Le kangourou est le seul gros animal à utiliser le saut pour la locomotion, mais le choc lors du saut est amorti par la flexion de ses pattes postérieures à chaque saut. (Voir Figure 3.)

Figure 3. Le travail effectué par le sol sur le kangourou réduit son énergie cinétique à zéro lorsqu’il atterrit. Cependant, en appliquant la force du sol sur les pattes postérieures sur une plus longue distance, l’impact sur les os est réduit. (crédit: Chris Samuel, Flickr)

Exemple 2. Trouver la vitesse d’une montagne russe à partir de sa hauteur

1. Quelle est la vitesse finale de la montagne russe illustrée à la figure 4 si elle part du repos au sommet de la colline de 20,0 m et si le travail effectué par les forces de frottement est négligeable?
2. Quelle est sa vitesse finale (encore une fois en supposant un frottement négligeable) si sa vitesse initiale est de 5,00 m/s ?

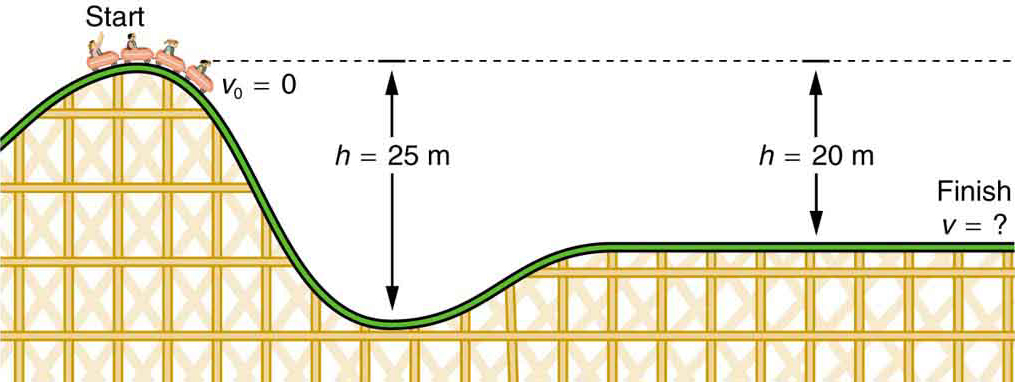
Figure 4. La vitesse d’une montagne russe augmente à mesure que la gravité la tire vers le bas et est la plus élevée à son point le plus bas. Vu en termes d’énergie, l’énergie potentielle gravitationnelle du système de montagnes russes-Terre est convertie en énergie cinétique. Si le travail effectué par frottement est négligeable, tout ΔPEg est converti en KE.

Stratégie

Les montagnes russes perdent de l’énergie potentielle en descendant. Nous négligeons le frottement, de sorte que la force restante exercée par la piste est la force normale, qui est perpendiculaire à la direction du mouvement et ne fonctionne pas. Le travail au filet sur les montagnes russes se fait alors par gravité seule. La perte d’énergie potentielle gravitationnelle due au déplacement vers le bas sur une distance h est égale au gain d’énergie cinétique. Cela peut s’écrire sous forme d’équation comme −ΔPEg = ΔKE. En utilisant les équations pour PEg et KE, nous pouvons résoudre pour la vitesse finale v, qui est la quantité souhaitée.

Solution pour la partie 1

Ici, l’énergie cinétique initiale est nulle, de sorte que \Delta\text{KE} = \frac{1}{2}mv^2\\. L’équation du changement d’énergie potentielle indique que ΔPEg = mgh. Puisque h est négatif dans ce cas, nous allons réécrire cela en ΔPEg = -mg / h / pour montrer clairement le signe moins. Ainsi, -ΔPEg = ΔKE devient mg/h/= \frac{1}{2}{mv}^2\\.

En résolvant pour v, nous trouvons que la masse s’annule et que v =\sqrt{2g/h/}\\.

En remplaçant les valeurs connues,

\begin{array}{lll}v &&\sqrt{2\left(9.80\text{m/s}^2\right)\left(20.0\ texte {m}\right)}\\\text {}&& 19.8 \text{m/s}\end{array}\\

Solution pour la partie 2

Encore − ΔPEg= ΔKE. Dans ce cas, il y a une énergie cinétique initiale, donc

\Delta\text{KE} = \frac{1}{2} mv^2-\frac{1}{2} mv_0^2\\.

Ainsi, mg/h/= \frac{1}{2} mv^2-\frac{1}{2} mv_0^2\\.

Le réarrangement donne \frac{1}{2} mv^2 = mg/h/+\frac{1}{2} mv +0^2\\.

Cela signifie que l’énergie cinétique finale est la somme de l’énergie cinétique initiale et de l’énergie potentielle gravitationnelle. La masse s’annule à nouveau, et v = \sqrt {2g/h/+v_0^2}\\.

Cette équation est très similaire à l’équation cinématique v = \sqrt{v_0^2 + 2ad}\\, mais elle est plus générale — l’équation cinématique n’est valable que pour une accélération constante, alors que notre équation ci-dessus est valable pour n’importe quel chemin, que l’objet se déplace ou non avec une accélération constante. Maintenant, la substitution de valeurs connues donne

\begin{array}{lll} v &&\sqrt{2\left(9.80\text{m/s}^2\right)\left(20.0\text{m}\ à droite) +\left(5.00\text {m/s}\right) ^2}\\\text {} &&20.4\text{m/s}\end{array}\\

Discussion et implications

Tout d’abord, notez que la masse s’annule. Ceci est tout à fait cohérent avec les observations faites dans les objets en chute selon lesquelles tous les objets tombent à la même vitesse si le frottement est négligeable. Deuxièmement, seule la vitesse des montagnes russes est prise en compte; il n’y a aucune information sur sa direction à aucun moment. Cela révèle une autre vérité générale. Lorsque le frottement est négligeable, la vitesse d’un corps tombant ne dépend que de sa vitesse et de sa hauteur initiales, et non de sa masse ou de la trajectoire empruntée. Par exemple, les montagnes russes auront la même vitesse finale qu’elles descendent de 20,0 m tout droit ou qu’elles empruntent un chemin plus compliqué comme celui de la figure. Troisièmement, et peut-être de manière inattendue, la vitesse finale de la partie 2 est supérieure à celle de la partie 1, mais de loin inférieure à 5,00 m / s. Enfin, notez que la vitesse peut être trouvée à n’importe quelle hauteur en cours de route en utilisant simplement la valeur appropriée de h au point d’intérêt.

Making Connections:Take-Home Investigation — Conversion du potentiel en Énergie cinétique

On peut étudier la conversion de l’énergie potentielle gravitationnelle en énergie cinétique dans cette expérience. Sur une surface lisse et plane, utilisez une règle du type qui a une rainure sur toute sa longueur et un livre pour faire une inclinaison (voir Figure 5). Placez un marbre à la position de 10 cm sur la règle et laissez-le rouler sur la règle. Lorsqu’il touche la surface plane, mesurez le temps nécessaire pour rouler d’un mètre. Maintenant, placez le marbre aux positions de 20 cm et de 30 cm et mesurez à nouveau le temps nécessaire pour rouler 1 m sur la surface plane. Trouvez la vitesse du marbre sur la surface plane pour les trois positions. Vitesse du tracé au carré par rapport à la distance parcourue par le marbre. Quelle est la forme de chaque parcelle? Si la forme est une ligne droite, le tracé montre que l’énergie cinétique du marbre au fond est proportionnelle à son énergie potentielle au point de libération.

Figure 5. Un marbre roule sur une règle et sa vitesse sur la surface plane est mesurée.

Questions conceptuelles

1. Dans l’exemple 2, nous avons calculé la vitesse finale d’une montagne russe qui descendait de 20 m de hauteur et avait une vitesse initiale de 5 m/s en descente. Supposons que les montagnes russes aient eu une vitesse initiale de 5 m / s en montée à la place, et qu’elles soient montées en montée, arrêtées, puis redescendues jusqu’à un point final à 20 m en dessous du départ. Nous trouverions dans ce cas qu’il avait la même vitesse finale. Expliquer en termes de conservation de l’énergie.
2. Le travail que vous faites sur un livre lorsque vous le soulevez sur une étagère dépend-il du chemin parcouru? Sur le temps pris ? Sur la hauteur de l’étagère? Sur la masse du livre?

Problèmes&Exercices

1. Une centrale hydroélectrique (voir Figure 6) convertit l’énergie potentielle gravitationnelle de l’eau derrière un barrage en énergie électrique. (a) Quelle est l’énergie potentielle gravitationnelle par rapport aux générateurs d’un lac de volume 50.0 km3 (masse = 5,00 × 1013 kg), étant donné que le lac a une hauteur moyenne de 40,0 m au-dessus des générateurs? b) Comparez cela avec l’énergie stockée dans une bombe à fusion de 9 mégatonnes.
   

   Figure 6. Installation hydroélectrique (crédit: Denis Belevich, Wikimedia Commons)

2. (a) Combien d’énergie potentielle gravitationnelle (par rapport au sol sur lequel elle est construite) est stockée dans la Grande Pyramide de Khéops, étant donné que sa masse est d’environ 7 × 109 kg et son centre de masse est de 36.5 m au-dessus du sol environnant ? b) Comment cette énergie se compare-t-elle à l’apport alimentaire quotidien d’une personne?
3. Supposons qu’un kookaburra de 350 g (un gros martin-pêcheur) ramasse un serpent de 75 g et le soulève à 2,5 m du sol jusqu’à une branche. a) Combien de travail l’oiseau a-t-il fait sur le serpent? b) Combien de travail a-t-il fait pour élever son propre centre de masse à la branche?
4. Dans l’exemple 2, nous avons constaté que la vitesse d’une montagne russe qui avait descendu 20,0 m n’était que légèrement supérieure lorsqu’elle avait une vitesse initiale de 5,00 m/s qu’au départ du repos. Cela implique que ΔPE >>KEi. Confirmez cette affirmation en prenant le rapport de ΔPE à KEi. (Notez que la masse s’annule.)
5. Une voiture jouet de 100 g est propulsée par un ressort comprimé qui la met en mouvement. La voiture suit la voie courbe de la figure 7. Montrer que la vitesse finale de la voiture-jouet est de 0,687 m / s si sa vitesse initiale est de 2,00 m / s et qu’elle remonte la pente sans frottement, gagnant 0,180 m d’altitude.
   

   Figure 7. Une voiture-jouet monte sur une piste en pente. (crédit: Leszek Leszczynski, Flickr)

6. Dans une course de ski alpin, étonnamment, peu d’avantage est obtenu en prenant un départ en course. (En effet, l’énergie cinétique initiale est faible par rapport au gain d’énergie potentielle gravitationnelle même sur de petites collines.) Pour le démontrer, trouvez la vitesse finale et le temps nécessaire pour un skieur qui survole 70,0 m le long d’une pente de 30º en négligeant les frottements : (a) En partant du repos. (b) En commençant par une vitesse initiale de 2,50 m/s. (c) La réponse vous surprend-elle? Expliquez pourquoi il est toujours avantageux de commencer à courir dans des événements très compétitifs.

Solutions sélectionnées aux problèmes &Exercices

1. (a) 1,96 × 1016 J; (b) Le rapport entre l’énergie potentielle gravitationnelle dans le lac et l’énergie stockée dans la bombe est de 0,52. Autrement dit, l’énergie stockée dans le lac est environ la moitié de celle d’une bombe à fusion de 9 mégatonnes.

3. (a) 1,8 J; (b) 8,6 J

5. {v}_{f} = \sqrt{2gh +{v_0}^2} = \sqrt{2\left(9,80\text{m/s}^2\right)\left(-0,180\text{m}\right) +\left(2,00\text{m/s}\right) ^2} = 0,687\text{m/s}\\