Konigsberg est une ville sur la rivière Preger, qui au 18ème sièclea été une ville allemande, mais est maintenant russe. Au sein de la ville se trouvent deuxles îles du fleuve qui sont reliées aux rives par sept ponts (comme indiqué ci-dessous).

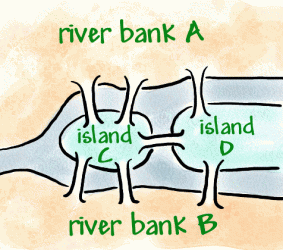
Il est devenu une tradition d’essayer de se promener dans la ville de manière à ne traverser chaque pont qu’une seule fois, mais cela s’est avéré être un problème difficile. Leonhard Euler, un mathématicien suisse au service del’impératrice russe Catherine la Grande, a entendu parler du problème.En 1736, Euler a prouvé que la promenade n’était pas possible. Il a amélioré cela en inventant une sorte de diagramme appelé réseau, composé de sommets (points où les lignes se rencontrent) et d’arcs (lignes).

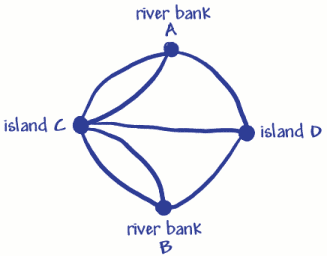
Il a utilisé quatre points (sommets) pour les deux rives et les deux terres. Ceux-ci ont été marqués A, B et C, D. Les sept lignes (arcs) sont les sept ponts. Vous pouvez voir que 3 ponts (arcs) rejoignent la rive A et 3 rejoignent la rive B. 5 ponts (arcs) rejoignent l’île C et 3 rejoignent l’île D. Cela signifie que tous les sommets ont un nombre impair d’arcs, ils sont donc appelés sommets impairs. (Un sommet pair devrait avoir un nombre pair d’arcs se joignant à lui).
Rappelez-vous que le problème était de parcourir la ville en traversant chaque pont une seule fois. Sur le réseau d’Euler, cela signifiait tracer sur chaque carré une seule fois, en visitant tous les sommets. Euler a prouvé que cela ne pouvait pas être fait parce qu’il a compris que pour avoir un sommet impair, vous deviez commencer ou terminer le voyage à ce sommet. (Pensez-y).Puisqu’il ne peut y avoir qu’un début et une fin, il ne peut y avoir que deux sommets impairs si vous ne pouvez tracer sur chacun qu’une seule fois. Comme le problème du pont a 4 sommets impairs, il n’est pas possible de le faire! Que se passe-t-il s’il n’y a pas de sommets impairs? Ce réseau peut-il être tracé ?

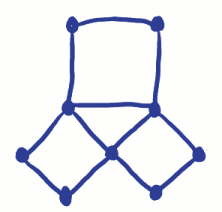
L’invention des réseaux a commencé un tout nouveau type de géométrie appelé topologie. La topologie est maintenant utilisée de nombreuses façons, y compris pour la planification et la cartographie des réseaux ferroviaires. (Ahhh! Les trains devaient entrer….)