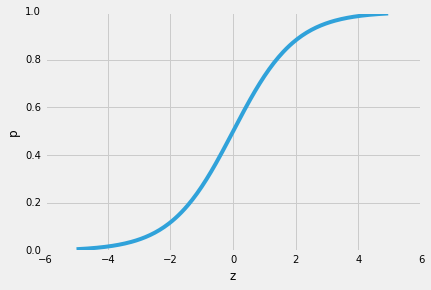
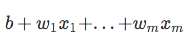Ainsi, l’une des propriétés intéressantes de la régression logistique est que la fonction sigmoïde génère les probabilités conditionnelles de la prédiction, les probabilités de classe. Comment ça marche?Commençons par le soi-disant « rapport de cotes” p / (1-p), qui décrit le rapport entre la probabilité qu’un certain événement positif se produise et la probabilité qu’il ne se produise pas – où positif se réfère à « l’événement que nous voulons prédire”, c’est-à-dire p (y = 1 | x).
(Notez que la régression logistique est un type particulier de fonction sigmoïde, la sigmoïde logistique; d’autres fonctions sigmoïdes existent, par exemple, la tangente hyperbolique).
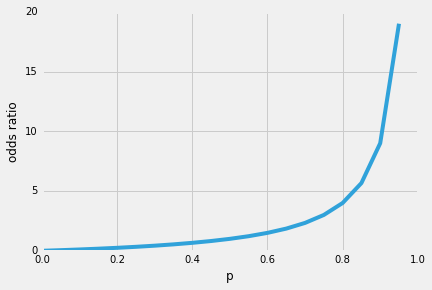
Ainsi, plus il est probable que l’événement positif se produise, plus le rapport de cotes est élevé.Maintenant, si nous prenons le journal naturel de ce rapport de cotes, la fonction log-odds ou logit, nous obtenons la
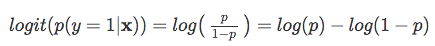
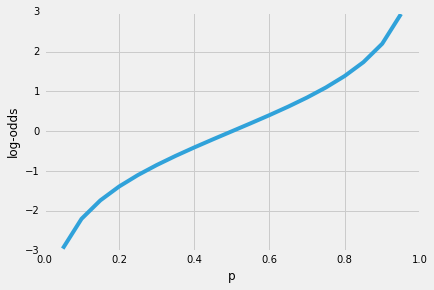
Ensuite, utilisons cette transformation de journal pour modéliser la relation entre nos variables explicatives et la variable cible:
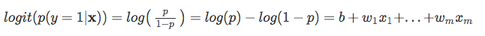
| Maintenant, gardez à l’esprit que nous n’essayons pas de prédire la bonne partie de l’équation ci-dessus, puisque *p(y = 1 | x) * est ce qui nous intéresse vraiment. So, let’s take the inverse of this logit function … et viola, we get the logistic sigmoid: |
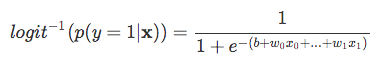
| which returns the class probabilities *p(y=1 | x)* from the inputs |