Après avoir compris la fonction exponentielle, notre prochaine cible est le logarithme naturel.

Étant donné la façon dont le journal naturel est décrit dans les livres de mathématiques, il y a peu de « naturel” à ce sujet: il est défini comme l’inverse deee ^x$, un exposant déjà assez étrange.

Mais il y a une explication nouvelle et intuitive: le journal naturel vous donne le temps nécessaire pour atteindre un certain niveau de croissance.

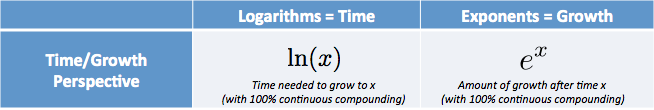
Supposons que vous ayez un investissement dans les ours gommeux (qui ne le fait pas?) avec un taux d’intérêt de 100% par an, en croissance continue. Si vous voulez une croissance 10x, en supposant une composition continue, vous n’attendriez que 2\ln(10) or ou 2,302 ans. Vous ne voyez pas pourquoi il ne faut que quelques années pour obtenir une croissance 10x? Vous ne voyez pas pourquoi le motif n’est pas 1, 2, 4, 8? En savoir plus sur e.

e et le journal naturel sont des jumeaux:

• ee^x is est le montant que nous avons après avoir commencé à 1.0 et en croissance continue pour $x$ unités de temps
• $\ln(x)$ (Logarithme Naturel) est le temps nécessaire pour atteindre un montant de $x$, en supposant que l’on a constamment augmenté de 1,0

Pas trop mal, non? Pendant que les mathématiciens se démènent pour vous donner la longue explication technique, plongeons dans l’explication intuitive.

E concerne la croissance

Le nombre e concerne la croissance continue. Comme nous l’avons vu la dernière fois,ee ^ x lets nous permet de fusionner le taux et le temps: 3 ans à 100% de croissance sont les mêmes que 1 an à 300% de croissance, lorsqu’ils sont composés en continu.

Nous pouvons prendre n’importe quelle combinaison de taux et de temps (50% pendant 4 ans) et convertir le taux en 100% pour plus de commodité (nous donnant 100% pendant 2 ans). En convertissant à un taux de 100%, il suffit de penser à la composante temps:

Intuitivement,ee^x means signifie:

• Combien de croissance ai-je après x unités de temps (et 100% de croissance continue)
• Par exemple: après 3 périodes de temps, j’aiee ^ 3 = = 20,08 fois la quantité de « choses”.

$e^x is est un facteur d’échelle, nous montrant combien de croissance nous obtiendrions après $x units unités de temps.

Le Log naturel est À propos du temps

Le log naturel est l’inverse deee^x$, un terme de fantaisie pour opposé. En parlant de fantaisie, le nom latin est logarithmus naturali, donnant l’abréviation ln.

Maintenant, que signifie ce truc inverse ou opposé?

• ee^x lets nous permet de prendre du temps et d’obtenir de la croissance.
• \\ln(x) lets nous permet de brancher la croissance et d’obtenir le temps qu’il faudrait.

Par exemple :

• ee^3 is vaut 20,08. Après 3 unités de temps, nous nous retrouvons avec 20.08 fois ce avec quoi nous avons commencé.
• \\ln(20.08) is est d’environ 3. Si nous voulons une croissance de 20,08, nous attendrions 3 unités de temps (encore une fois, en supposant un taux de croissance continu de 100%).

Avec moi ? La bûche naturelle nous donne le temps nécessaire pour atteindre notre croissance désirée.

L’arithmétique logarithmique N’est Pas Normale

Vous avez déjà étudié les journaux, et c’étaient des bêtes étranges. Comment ont-ils transformé la multiplication en addition? Division en soustraction? Voyons voir.

Qu’est-ce que $\ln(1)$? Intuitivement, la question est: Combien de temps dois-je attendre pour obtenir 1x mon montant actuel?

Zéro. Zip. NADA. Vous êtes déjà à 1x votre montant actuel! Cela ne prend pas de temps pour passer de 1 à 1.

• $\ln(1) = 0Ok

Ok, que diriez-vous d’une valeur fractionnaire? Combien de temps pour obtenir 1/2 de mon montant actuel? En supposant que vous croissez continuellement à 100%, nous savons que\\ln(2) is est le temps à doubler. Si nous l’inversons (c’est-à-dire, prenons le temps négatif), nous aurions la moitié de notre valeur actuelle.

• $\ln(.5) = – \ln(2) =-.693Makes

Est logique, non? Si on recule.693 unités (secondes négatives, disons) nous aurions la moitié de notre montant actuel. En général, vous pouvez retourner la fraction et prendre le négatif:\\ln(1/3) = –\ln(3) = -1,09$. Cela signifie que si nous revenons à 1,09 unité de temps, nous aurions un tiers de ce que nous avons maintenant.

Ok, que diriez-vous du journal naturel d’un nombre négatif? Combien de temps faut-il pour « faire croître” votre colonie de bactéries de 1 à -3?

C’est impossible ! Vous ne pouvez pas avoir une quantité ”négative » de bactéries, n’est-ce pas? Au plus (euh least au moins) vous pouvez avoir zéro, mais il n’y a aucun moyen d’avoir une quantité négative des petites bestioles. Les bactéries négatives n’ont tout simplement pas de sens.

• $\ln(\text{nombre négatif}) = \text{undefined}Und

Undefined signifie simplement « il n’y a pas de temps que vous pouvez attendre” pour obtenir un montant négatif. (Eh bien, si nous utilisons des exponentielles imaginaires, il existe une solution. Mais aujourd’hui, gardons cela réel.)

La multiplication logarithmique est très amusante

Combien de temps faut-il pour augmenter de 9 fois votre montant actuel? Bien sûr, nous pourrions simplement utiliser ln(9). Mais c’est trop facile, soyons différents.

Nous pouvons considérer la croissance 9x comme un triplement (en prenant $\ln(3) units unités de temps) puis en triplant à nouveau (en prenant un autre units\ln(3) units unités de temps):

• Temps de croissance 9x = Time\ln(9) ==Temps de tripler et de tripler à nouveau =Interesting\ln(3) +\ln(3)Interesting

Intéressant. Tout nombre de croissance, comme 20, peut être considéré comme une croissance 2x suivie d’une croissance 10x. Soit une croissance 4x suivie d’une croissance 5x. Soit une croissance 3x suivie d’une croissance 6.666x. Vous voyez le motif ?

• $\ln(a*b) = \ln(a) + \ln(b)The

Le journal d’une fois b = log(a) + log(b). Cette relation a du sens lorsque vous pensez en termes de temps pour grandir.

Si nous voulons grandir, 30x, nous pouvons attendre que $\ln(30)$ tout à la fois, ou tout simplement attendre que $\ln(3)$, triple, puis attendez que $\ln(10)$, de grandir 10x à nouveau. L’effet net est le même, donc le temps net devrait être le même aussi (et c’est le cas).

Qu’en est-il de la division? means\ln(5/3) means signifie: Combien de temps faut-il pour croître 5 fois et en prendre ensuite 1/3?

Eh bien, la croissance 5 fois est $\ln(5)$. La croissance de 1/3 est $-\ln(3) units unités de temps. Donc

• So\ln(5/3) = \ln(5)– \ln(3)Which

Qui dit: Croissez 5 fois et « remontez dans le temps” jusqu’à ce que vous ayez un tiers de cette quantité, donc vous vous retrouvez avec une croissance de 5/3. En général, nous avons

• $\ln(a /b) = \ln–a)- \ln(b)

J’espère que les mathématiques étranges des logarithmes commencent à avoir du sens: la multiplication de la croissance devient addition du temps, la division de la croissance devient soustraction du temps. Ne mémorisez pas les règles, comprenez-les.

Utiliser des journaux naturels Avec n’importe quel Taux

« Bien sûr,”dites-vous, « Ce journal fonctionne pour une croissance de 100%, mais qu’en est-il des 5% que j’obtiens normalement?”

Ce n’est pas un problème. Le « temps » que nous revenons de $\ln() is est en fait une combinaison de taux et de temps, le « x » de notre équationee^x equation. Nous supposons juste 100% pour le rendre simple, mais nous pouvons utiliser d’autres nombres.

Supposons que nous voulons une croissance 30x: branchez $\ln(30) and et obtenez 3.4. Cela signifie:

• $e^x =\text{growth}
• ee^{3.4} = 30And

Et intuitivement, cette équation signifie « 100% de rendement pour 3,4 ans est une croissance de 30x”. On peut considérer l’équation comme :

Nous pouvons modifier « rate” et « time”, tant que rate*time = 3.4. Par exemple, supposons que nous souhaitions une croissance de 30 fois – combien de temps attendons-nous en supposant un rendement de 5%?

• $\ln(30) = 3,4
• \\text{rate} *\text{time} = 3.4
• $.05*\text{time} = 3.4
• \\text{time} = 3.4/.05 = 68 \text {years}Intu

Intuitivement, je pense « \\ln(30) = 3,4,, donc à 100% de croissance, cela prendra 3,4 ans. Si je double le taux de croissance, je divise par deux le temps nécessaire. »

• 100% pendant 3,4 ans = 1,0 *3,4= 3,4
• 200% pendant 1,7 ans = 2,0 * 1,7 = 3,4
• 50% pendant 6,8 ans = 0,5 *6,8= 3,4
• 5% pendant 68 ans =.05 * 68 = 3,4

Cool, hein? Le journal naturel peut être utilisé avec n’importe quel taux d’intérêt ou temps tant que leur produit est le même. Vous pouvez remuer les variables tout ce que vous voulez.

Exemple génial: La Règle de 72

La Règle de 72 est un raccourci mathématique mental pour estimer le temps nécessaire pour doubler votre argent. Nous allons le dériver (yay!) et encore mieux, nous allons le comprendre intuitivement.

Combien de temps faut-il pour doubler votre argent à 100% d’intérêt, composé chaque année?

Euh oh. Nous avons utilisé le journal naturel pour les taux continus, mais maintenant vous demandez des intérêts annuels? Cela ne va-t-il pas gâcher notre formule? Oui, mais à des taux d’intérêt raisonnables comme 5%, 6% ou même 15%, il n’y a pas beaucoup de différence entre les intérêts composés annuels et les intérêts entièrement continus. Donc, la formule approximative fonctionne, euh, à peu près et nous ferons comme si nous recevions un intérêt continu.

Maintenant, la question est facile: Combien de temps doubler à 100% d’intérêt? ln(2) =.693. Ça prend.693 unités de temps (années, dans ce cas) pour doubler votre argent avec une composition continue avec un taux de 100%.

Ok, et si notre intérêt n’est pas à 100% Et si c’est 5% ou 10%?

Simple. Tant que rate * time =.693, nous doublerons notre argent :

• rate*time=.693
• temps =.693/rate

Donc, si nous n’avions que 10% de croissance, cela prendrait.693 / .10 ou 6,93 ans à doubler.

Pour simplifier les choses, multiplions par 100 pour pouvoir parler de 10 plutôt que.10:

• temps à doubler = 69,3 / taux, où le taux est supposé être en pourcentage.

Maintenant, le temps de doubler à 5% de croissance est de 69,3 / 5 ou 13,86 ans. Cependant, 69,3 n’est pas le nombre le plus divisible. Choisissons un voisin proche, 72, qui peut être divisé par 2, 3, 4, 6, 8 et bien d’autres nombres.

• temps à doubler = 72/taux

qui est la règle de 72! Légère brise.

Si vous voulez trouver le temps de tripler, vous utiliserez ln(3) ~ 109.8 et obtiendrez

• time to triple = 110/rate

Qui est une autre règle empirique utile. La règle de 72 est utile pour les taux d’intérêt, la croissance de la population, les cultures de bactéries et tout ce qui croît de manière exponentielle.

Où aller d’ici ?

J’espère que le journal naturel a plus de sens — il vous indique le temps nécessaire pour toute quantité de croissance exponentielle. Je le considère comme « naturel » parce que e est le taux de croissance universel, donc ln pourrait être considéré comme le moyen ”universel » de comprendre combien de temps les choses prennent pour croître.

Lorsque vous voyez $\ln(x),, pensez simplement « le temps nécessaire pour atteindre x »” Dans le prochain article, nous réunirons e et ln, et le doux arôme des mathématiques remplira l’air.

Annexe: Le journal naturel de E

Quiz rapide: Qu’est-ce que $\ln(e)$?

• Le robot mathématique dit: Parce qu’ils sont définis comme des fonctions inverses, clairement $\ln(e) =1
• L’humain intuitif: ln(e) est le temps qu’il faut pour obtenir des unités de croissance « e” (environ 2,718). Mais e est la quantité de croissance après 1 unité de temps, donc $\ln(e) = 1$.

Pensez intuitivement.

Autres Articles De Cette Série

1. Un Guide Intuitif Des Fonctions Exponentielles &e
2. Démystifier le Logarithme Naturel (ln)
3. Un Guide Visuel des Taux d’Intérêt Simples, Composés et Continus
4. Définitions Communes de e (Colorisé)
5. Comprendre les Exposants (Pourquoi 0^ 0 = 1?)
6. Utiliser les Logarithmes dans le Monde Réel
7. Comment Penser Avec Les Exposants Et Les Logarithmes
8. Comprendre La Croissance Discrète par rapport À la Croissance Continue
9. Que signifie vraiment un exposant?
10. Q: Pourquoi e est-il spécial? (2.718…, pas 2, 3,7 ou un autre numéro?)