Dans d’autres sections, il a été mentionné que de nombreuses propriétés des solides, des liquides et des gaz pourraient être prises en compte si nous supposions que les substances sont constituées d’atomes ou de molécules constamment en mouvement. La loi de Boyle et les autres lois sur les gaz nous ont maintenant donné beaucoup plus d’informations quantitatives sur les gaz, et il convient de se demander si, avec le modèle précédent, nous pouvons faire des prédictions quantitatives en accord avec ces lois. En répondant à cette question, nous obtiendrons également des informations importantes sur la nature de la température et de l’énergie thermique.
La théorie microscopique du comportement des gaz basée sur le mouvement moléculaire s’appelle la théorie cinétique des gaz. Ses postulats de base sont énumérés dans le tableau 1:
TABLEAU \(\PageIndex{1}\) Postulats de la Théorie Cinétique des gaz.
1 Les molécules d’un gaz sont petites et très éloignées les unes des autres. La majeure partie du volume qu’occupe un gaz est un espace vide.
2 molécules de gaz sont en mouvement aléatoire constant. Autant de molécules se déplacent dans une direction que dans n’importe quelle autre.
3 molécules peuvent entrer en collision les unes avec les autres et avec les parois du récipient. Les collisions avec les parois expliquent la pression du gaz.
4 Lorsque des collisions se produisent, les molécules ne perdent aucune énergie cinétique; c’est-à-dire que les collisions sont dites parfaitement élastiques. L’énergie cinétique totale de toutes les molécules reste constante à moins qu’il n’y ait une interférence extérieure avec les
5 Les molécules n’exercent aucune force attractive ou répulsive les unes sur les autres, sauf pendant le processus de collision. Entre les collisions, ils se déplacent en ligne droite.
On peut en déduire l’expression suivante de la pression d’un gaz en fonction des propriétés de ses molécules :
\Où P, V = pression et volume du gaz
N = nombre de molécules
m = masse de chaque molécule
(u2)ave = moyenne (ou moyenne) des carrés de toutes les vitesses moléculaires individuelles. Cette vitesse carrée moyenne doit être utilisée car la pression est proportionnelle au carré de la vitesse moléculaire et les collisions moléculaires font que différentes molécules ont des vitesses très différentes.
Plutôt que de nous préoccuper de la procédure pour dériver Eq. \(\ref{1} \), inspectons l’équation et voyons que ses caractéristiques générales sont tout à fait ce à quoi nous nous attendions. À certains égards, la capacité de le faire avec une formule est plus utile que la capacité de la dériver. Figure \(\PageIndex{1}\)
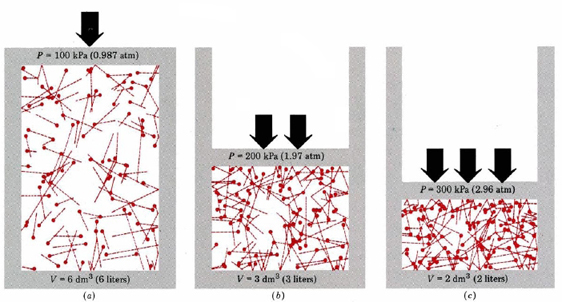 Tout d’abord, l’équation nous dit que la pression d’un gaz est proportionnelle au nombre de molécules divisé par le volume. Ceci est illustré graphiquement dans la figure \(\PageIndex{1}\), où un ordinateur a dessiné le même nombre de molécules de gaz occupant chacun de trois volumes différents. La « queue » de chaque molécule indique le chemin exact suivi par cette molécule au cours de la microseconde précédente — plus la queue est longue, plus la molécule allait vite. La moyenne des carrés des longueurs de queue est proportionnelle à (u2) ave et est la même dans les trois diagrammes. On suppose également que toutes les molécules ont des masses égales.
Tout d’abord, l’équation nous dit que la pression d’un gaz est proportionnelle au nombre de molécules divisé par le volume. Ceci est illustré graphiquement dans la figure \(\PageIndex{1}\), où un ordinateur a dessiné le même nombre de molécules de gaz occupant chacun de trois volumes différents. La « queue » de chaque molécule indique le chemin exact suivi par cette molécule au cours de la microseconde précédente — plus la queue est longue, plus la molécule allait vite. La moyenne des carrés des longueurs de queue est proportionnelle à (u2) ave et est la même dans les trois diagrammes. On suppose également que toutes les molécules ont des masses égales.
Comme vous pouvez le voir, la réduction du volume du gaz augmente le nombre de collisions par unité de surface sur les parois du conteneur. Chaque collision exerce une force sur le mur; la force par unité de surface est la pression, et le nombre de collisions par unité de surface est donc proportionnel à la pression. La réduction de moitié du volume double la pression, une prédiction qui concorde avec les faits expérimentaux résumés dans la loi de Boyle. L’équation \(\ref{1}\) dit également que la pression est proportionnelle à la masse de chaque molécule de gaz. Encore une fois, c’est ce à quoi nous nous attendions. Les molécules lourdes donnent une plus grande « poussée » (le terme technique pour cela est impulsion) contre le mur que les molécules légères avec la même vitesse.
Enfin, l’équation nous dit que la pression est proportionnelle à la moyenne des carrés des vitesses moléculaires. Cette dépendance au carré de vitesse est raisonnable si l’on se rend compte que doubler la vitesse d’une molécule a deux effets.
Tout d’abord, la molécule peut se déplacer plus loin dans un laps de temps donné, doublant le nombre de collisions avec les parois. Cela doublerait la pression. Deuxièmement, doubler la vitesse d’une molécule double la poussée ou l’impulsion de chaque collision. Cela double à nouveau la pression. Par conséquent, doubler la vitesse d’une molécule quadruple la pression, et pour un grand nombre de molécules, P est proportionnel à la vitesse quadratique moyenne.
Contributeurs
-
Ed Vitz (Université de Kutztown), John W. Moore (Université de Madison), Justin Shorb (Hope College), Xavier Prat-Resina (Université du Minnesota à Rochester), Tim Wendorff et Adam Hahn.