Loi de Boyle
Robert Boyle (1627 – 1691), un chimiste anglais, est largement considéré comme l’un des fondateurs de la science expérimentale moderne de la chimie. Il a découvert qu’en doublant la pression d’un échantillon de gaz enfermé tout en maintenant sa température constante, le volume du gaz était réduit de moitié. La loi de Boyle stipule que le volume d’une masse de gaz donnée varie inversement avec la pression lorsque la température est maintenue constante. Une relation inverse est ainsi décrite. Lorsque la valeur d’une variable augmente, l’autre variable diminue.
Physiquement, que se passe-t-il ? Les molécules de gaz se déplacent et sont à une certaine distance les unes des autres. Une augmentation de la pression rapproche les molécules, réduisant le volume. Si la pression diminue, les gaz sont libres de se déplacer dans un volume plus important.

Mathématiquement, la loi de Boyle peut être exprimée par l’équation:
\
Le \(k\) est une constante pour un échantillon donné de gaz et ne dépend que de la masse du gaz et de la température. Le tableau ci-dessous montre les données de pression et de volume pour une quantité définie de gaz à température constante. La troisième colonne représente la valeur de la constante \(\left(k\right)\) pour ces données et est toujours égale à la pression multipliée par le volume. Lorsque l’une des variables change, l’autre change de telle sorte que le produit de \(P\fois V\) reste toujours le même. Dans ce cas particulier, cette constante est \(500\:\text{atm}\cdot\text{mL}\).
| Pressure \(\left( \text{atm} \right)\) | Volume \(\left( \text{mL} \right)\) | \(P \times V = k\) \(\left( \text{atm} \cdot \text{mL} \right)\) |
|---|---|---|
| 0.5 | 1000 | 500 |
| 0.625 | 800 | 500 |
| 1.0 | 500 | 500 |
| 2.0 | 250 | 500 |
| 5.0 | 100 | 500 |
| 8.0 | 62.5 | 500 |
| 10.0 | 50 | 500 |
Un graphique des données dans le tableau illustre en outre la nature de la relation inverse de la loi de Boyle (voir figure ci-dessous). Le volume est tracé sur l’axe \(x\), avec la pression correspondante sur l’axe \(y\).
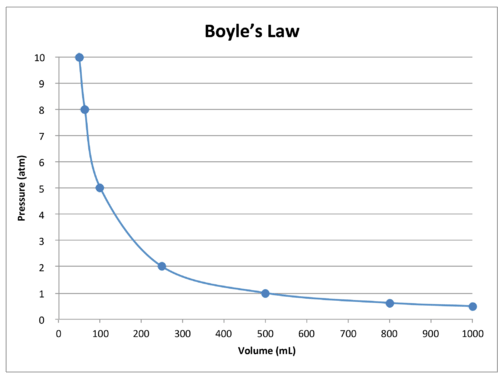
La loi de Boyle peut être utilisée pour comparer les conditions changeantes d’un gaz. Nous utilisons \(P_1\) et \(V_1\) pour représenter la pression initiale et le volume initial d’un gaz. Une fois qu’un changement a été effectué, \(P_2\) et \(V_2\) représentent la pression et le volume finaux. La relation mathématique de la loi de Boyle devient :
\
Cette équation peut être utilisée pour calculer n’importe laquelle des quatre grandeurs si les trois autres sont connues.
Exemple \(\PageIndex{1}\)
Un échantillon d’oxygène gazeux a un volume de \(425 \: \text{mL}\) lorsque la pression est égale à \(387\:\text{kPa}\). Le gaz est autorisé à se dilater dans un conteneur \(1.75\:\text{L}\). Calculez la nouvelle pression du gaz.
Solution
Étape 1: Listez les quantités connues et planifiez le problème.
Connu
- \(P_1= 387\:\text{kPa}\)
- \(V_1= 425\:\text{mL}\)
- \(V_2= 1,75\:\text{L}= 1750\:\text{mL}\)
Inconnu
- \( P_2 =? \:\text{kPa}\)
Utilisez la loi de Boyle pour résoudre la pression inconnue \(\left(P_2\right)\). Il est important que les deux volumes (\(V_1\) et \(V_2\)) soient exprimés dans les mêmes unités, donc \(V_2\) a été converti en \(\text{mL}\).
Étape 2: Résoudre.
Tout d’abord, réorganisez l’équation algébriquement pour la résoudre pour \(P_2\).
\
Maintenant, remplacez les quantités connues dans l’équation et résolvez.
\
Étape 3: Pensez à votre résultat.
Le volume a augmenté à un peu plus de 4 fois sa valeur d’origine et la pression est donc diminuée d’environ un quart. La pression est en \(\text{kPa}\) et la valeur a trois chiffres significatifs. Notez que toutes les unités de pression ou de volume peuvent être utilisées tant qu’elles sont cohérentes tout au long du problème.