Orbitales atomiques
Une orbitale est le raffinement mécanique quantique de l’orbite de Bohr. Contrairement à son concept d’orbite circulaire simple avec un rayon fixe, les orbitales sont des régions de l’espace dérivées mathématiquement avec différentes probabilités d’avoir un électron.
Une façon de représenter les distributions de probabilité des électrons a été illustrée à la figure 6.5.2 pour l’orbitale 1s de l’hydrogène. Comme Ψ2 donne la probabilité de trouver un électron dans un volume d’espace donné (tel qu’un picomètre cubique), un tracé de Ψ2 en fonction de la distance du noyau (r) est un tracé de la densité de probabilité. L’orbitale 1s est symétrique sphériquement, de sorte que la probabilité de trouver un électron 1s en un point donné ne dépend que de sa distance du noyau. La densité de probabilité est la plus élevée à r = 0 (au niveau du noyau) et diminue régulièrement avec l’augmentation de la distance. À de très grandes valeurs de r, la densité de probabilité électronique est très faible mais non nulle.
En revanche, on peut calculer la probabilité radiale (la probabilité de trouver un électron 1s à une distance r du noyau) en additionnant les probabilités qu’un électron soit en tous points d’une série de coquilles sphériques x de rayon r1, r2, r3,…, rx−1, rx. En effet, nous divisons l’atome en coquilles concentriques très fines, un peu comme les couches d’un oignon (partie (a) de la figure \(\PageIndex{1}\)), et calculons la probabilité de trouver un électron sur chaque coquille sphérique. Rappelons que la densité de probabilité d’électrons est la plus grande à r = 0 (partie (b) de la Figure \(\PageIndex{1}\)), donc la densité de points est la plus grande pour les plus petites coquilles sphériques de la partie (a) de la Figure \(\PageIndex{1}\). En revanche, la surface de chaque coquille sphérique est égale à 4nr2, ce qui augmente très rapidement avec l’augmentation de r (partie (c) de la figure \(\PageIndex{1}\)). Comme la surface des coquilles sphériques augmente plus rapidement avec l’augmentation de r que la densité de probabilité électronique ne diminue, le tracé de probabilité radiale a un maximum à une distance particulière (partie (d) de la figure \(\PageIndex{1}\)). Plus important encore, lorsque r est très petit, la surface d’une coquille sphérique est si petite que la probabilité totale de trouver un électron près du noyau est très faible; au niveau du noyau, la probabilité d’électron disparaît (partie (d) de la figure \(\PageIndex{1}\)).

Pour l’atome d’hydrogène, le pic dans le diagramme de probabilité radial se produit à r = 0,529 Å (52,9 pm), ce qui est exactement le rayon calculé par Bohr pour l’orbite n = 1. Ainsi, le rayon le plus probable obtenu à partir de la mécanique quantique est identique au rayon calculé par la mécanique classique. Dans le modèle de Bohr, cependant, l’électron était supposé être à cette distance 100% du temps, alors que dans le modèle de Schrödinger en mécanique quantique, il n’est à cette distance qu’une partie du temps. La différence entre les deux modèles est attribuable au comportement ondulatoire de l’électron et au principe d’incertitude de Heisenberg.
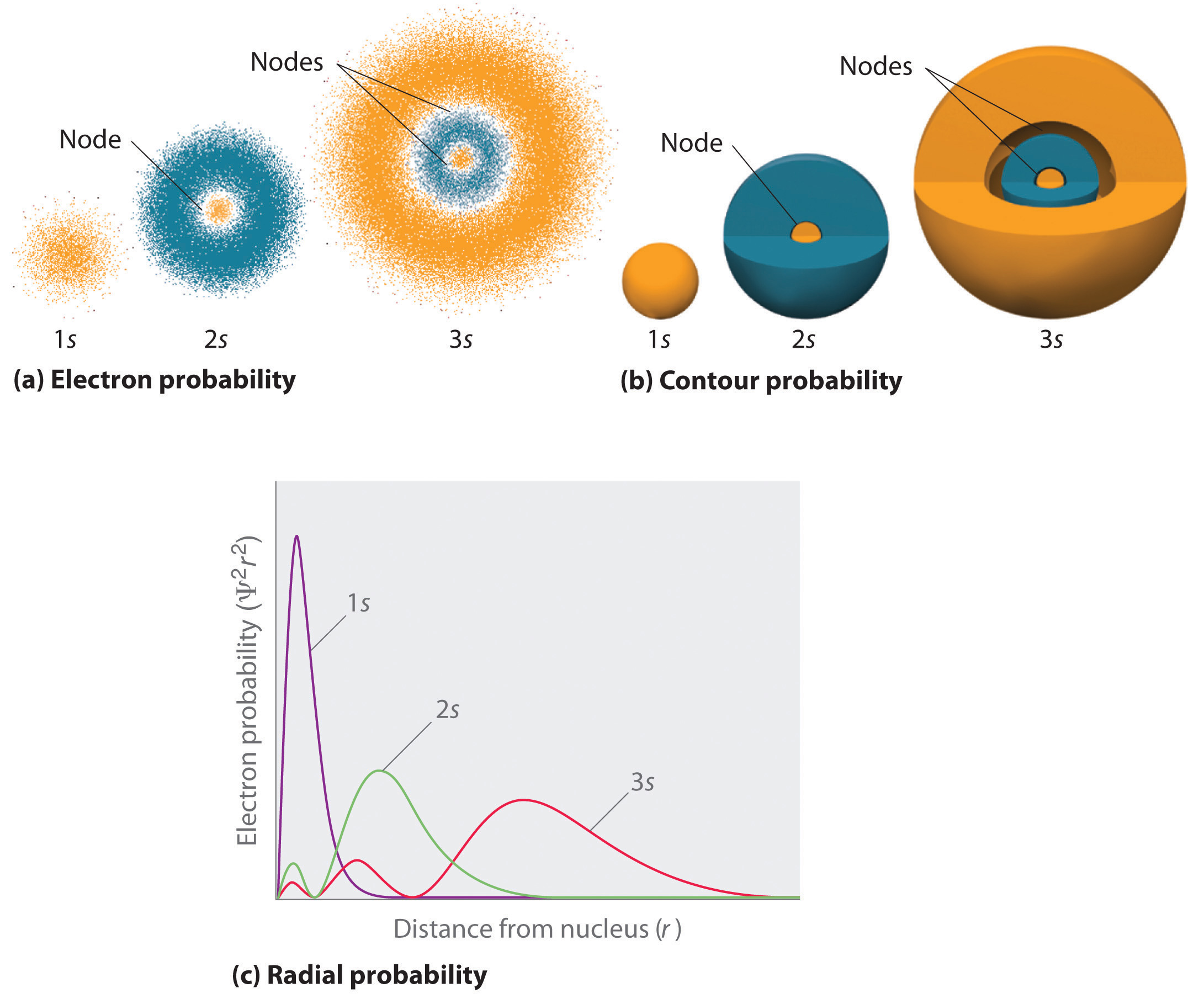
La figure \(\PageIndex{2}\) compare les densités de probabilité d’électrons pour les orbitales hydrogène 1s, 2s et 3s. Notez que tous les trois sont sphériquement symétriques. Pour les orbitales 2s et 3s, cependant (et pour toutes les autres orbitales s également), la densité de probabilité d’électrons ne diminue pas en douceur avec l’augmentation de r. Au lieu de cela, une série de minima et de maxima sont observés dans les diagrammes de probabilité radiaux (partie (c) de la figure \(\PageIndex{2}\)). Les minima correspondent à des nœuds sphériques (régions de probabilité d’électrons nulle), qui alternent avec des régions sphériques de probabilité d’électrons non nulle.