Lektion 3: komplexa formler
/en/excelformulas/simple-formulas/content/
Inledning
en enkel formel är ett matematiskt uttryck med en operatör, till exempel 7+9. En komplex formel har mer än en matematisk operatör, såsom 5+2*8. När det finns mer än en operation i en formel, berättar ordningsföljden ditt kalkylblad vilken operation som ska beräknas först. För att kunna använda komplexa formler måste du förstå operationsordningen.
valfritt: Ladda ner vår exempelfil för den här lektionen.
titta på videon nedan för att lära dig mer om komplexa formler.
operationsordningen
alla kalkylprogram beräknar formler baserat på följande operationsordning:
- operationer inneslutna inom parentes
- exponentiella beräkningar (3^2, till exempel)
- multiplikation och division, beroende på vilket som kommer först
- Addition och subtraktion, vilket som kommer först
en mnemonic som kan hjälpa dig att komma ihåg ordern är PEMDAS, eller snälla ursäkta min kära moster Sally.
klicka på pilarna i bildspelet nedan för att lära dig mer om hur ordningsföljden används för att beräkna komplexa formler.

även om denna formel kan se väldigt komplicerad ut, kan vi använda operationsordningen steg för steg för att hitta rätt svar.
-

först börjar vi med att beräkna något inom parenteserna. I det här fallet finns det bara en sak vi behöver beräkna: 6-3=3.
-

som du kan se ser formeln redan lite enklare ut. Därefter ska vi se om det finns några exponenter. Det finns en: 2^2 = 4.
-

därefter löser vi eventuell multiplikation och division, som arbetar från vänster till höger. Eftersom delningsoperationen kommer före multiplikationen beräknas den först: 3/4=0,75.
-

nu beräknar vi vår återstående multiplikationsoperation: 0.75*4=3.
-

därefter beräknar vi tillägg eller subtraktion, igen från vänster till höger. Tillägg kommer först: 10 + 3=13.
-

Slutligen har vi en återstående subtraktionsoperation: 13-1=12.
-

och nu har vi vårt svar: 12. Detta är exakt samma resultat som du skulle få om du angav formeln i ett kalkylblad.
-

att använda parenteser inom en formel kan vara mycket viktigt. På grund av operationsordningen kan det helt ändra ett svar. Låt oss försöka samma problem ovanifrån, men den här gången lägger vi till parenteser till den sista delen.
skapa komplexa formler
i exemplet nedan visar vi en komplex formel med hjälp av operationsordningen. Här vill vi beräkna kostnaden för moms för en cateringfaktura. För att göra detta skriver vi vår formel som =(D2+D3)*0,075 i cell D4. Denna formel kommer att lägga till priserna på våra artiklar tillsammans och sedan multiplicera det värdet med 7,5% skattesats (som skrivs som 0,075) för att beräkna kostnaden för moms.
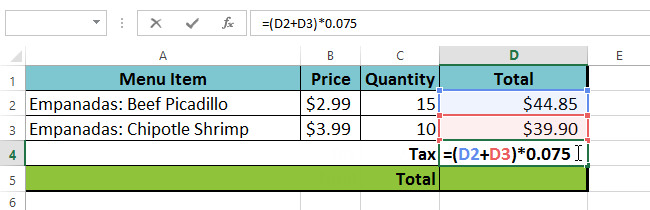
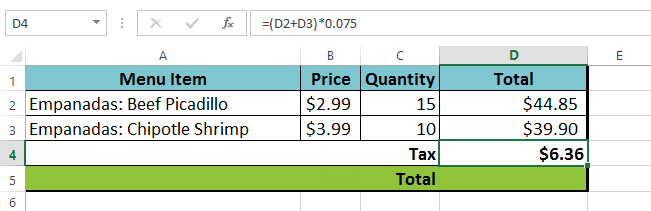
kalkylbladet följer sedan operationsordningen och lägger först till värdena inom parenteserna: (44.85+39.90) = $84.75. Sedan multiplicerar det värdet med skattesatsen: $84.75 * 0.075. Resultatet visar att försäljningsskatten är $6.36.
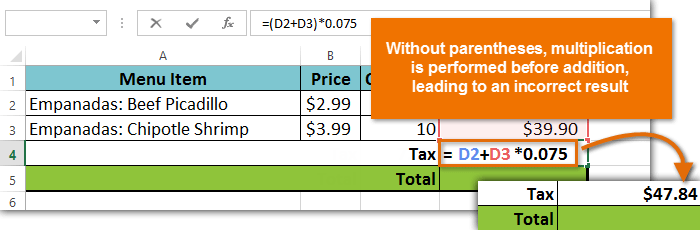
det är särskilt viktigt att ange komplexa formler med rätt ordningsföljd. Annars beräknar kalkylbladet inte resultaten exakt. I vårt exempel, om parenteserna inte ingår, beräknas multiplikationen först och resultatet är felaktigt. Parenteser är det bästa sättet att definiera vilka beräkningar som ska utföras först i en formel.
för att skapa en komplex formel med operationsordningen:
i vårt exempel nedan använder vi cellreferenser tillsammans med numeriska värden för att skapa en komplex formel som beräknar den totala kostnaden för en cateringfaktura. Formeln beräknar kostnaden för varje menyalternativ och lägger till dessa värden tillsammans.
- välj den cell som innehåller formeln. I vårt exempel väljer vi cell C4.
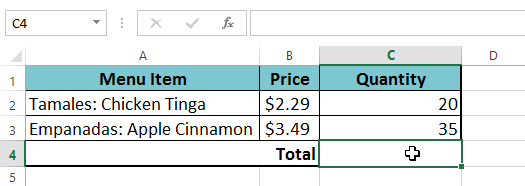
- ange din formel. I vårt exempel skriver vi =B2 * C2 + B3 * C3. Denna formel följer operationsordningen, som först utför multiplikation: 2,29*20 = 45,80 och 3,49 * 35 = 122,15. Då kommer det att lägga till dessa värden tillsammans för att beräkna summan: 45.80 + 122.15.
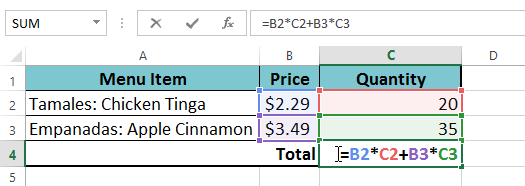
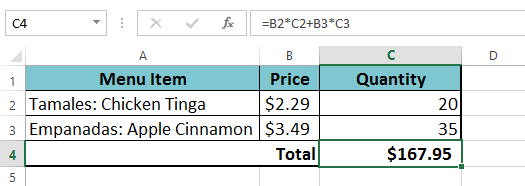
- dubbelkontrollera din formel för noggrannhet och tryck sedan på Enter på tangentbordet. Formeln beräknar och visar resultatet. I vårt exempel visar resultatet att den totala kostnaden för ordern är $167.95.
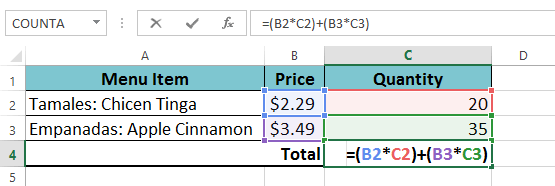
Du kan lägga till parenteser till någon ekvation för att göra det lättare att läsa. Även om det inte kommer att ändra resultatet av formeln i det här exemplet, kan vi bifoga multiplikationsoperationerna inom parentes för att klargöra att de kommer att beräknas före tillägget.
ditt kalkylblad kommer inte alltid att berätta om din formel innehåller Ett fel, så det är upp till dig att kontrollera alla dina formler. För att lära dig hur du gör detta, kolla in dubbelkolla dina formler lektion.
utmaning!
- öppna en befintlig Excel-arbetsbok. Om du vill kan du använda exempelfilen för den här lektionen.
- skapa en komplex formel som kommer att utföra tillägg före multiplikation. Om du använder exemplet skapar du en formel i cell D6 som först lägger till värdena för cellerna D3, D4 och D5 och multiplicerar sedan deras totala med 0,075. Tips: du måste tänka på ordningen för verksamheten för att detta ska fungera korrekt.