Algunas cosas interesantes sobre ángulos y círculos.
- Ángulo Inscrito
- Teoremas de Ángulo inscrito
- Ejemplo: ¿Cuál es el tamaño del Ángulo POQ? (O es el centro del círculo)
- Ejemplo: ¿Cuál es el tamaño del ángulo CBX?
- Ángulo en un Semicírculo (Teorema de Thales)
- Otra buena razón Por qué funciona
- Ejemplo: ¿Cuál es el tamaño del ángulo BAC?
- Encontrar el centro de un círculo
- Cuadrilátero Cíclico
- Ejemplo: ¿Cuál es el tamaño de Ángulo WXY?
Ángulo Inscrito
en Primer lugar, una definición:
Ángulo Inscrito: un ángulo desde puntos sentado sobre el círculo de la circunferencia.
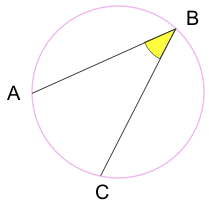
A y C son » puntos finales «
B es el»punto ápice «
Juegue con él aquí:
Cuando mueve el punto» B», ¿qué sucede con el ángulo?
Teoremas de Ángulo inscrito
Un ángulo inscrito a° es la mitad del ángulo central 2a°
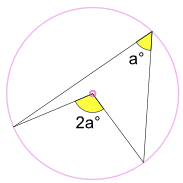
(Llamado el Teorema del Ángulo en el Centro)
Y (manteniendo los puntos finales fijos) …
… el ángulo a° es siempre el mismo,
no importa dónde esté en el mismo arco entre los puntos finales:
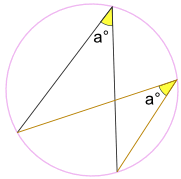
El ángulo a° es el mismo.
(Llamados Ángulos Subtendidos por el Mismo Teorema de Arco)
Ejemplo: ¿Cuál es el tamaño del Ángulo POQ? (O es el centro del círculo)
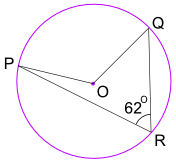
Ángulo POQ = 2 × Ángulo PRQ = 2 × 62° = 124°
Ejemplo: ¿Cuál es el tamaño del ángulo CBX?
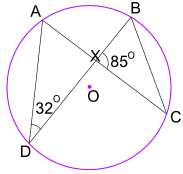
El ángulo ADB = 32 ° también equivale al ángulo ACB.
Y el ángulo ACB también es igual al Ángulo XCB.
Así que en el triángulo BXC sabemos que el Ángulo BXC = 85°, y el Ángulo XCB = 32 °
Ahora usamos los ángulos de un triángulo sumados a 180° :
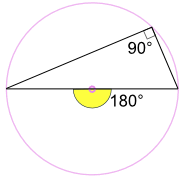
Ángulo en un Semicírculo (Teorema de Thales)
Un ángulo inscrito a través del diámetro de un círculo es siempre un ángulo recto:
(Los puntos finales son cualquiera de los extremos del diámetro de un círculo,
la circunferencia.)
|
¿por Qué? Porque: El ángulo inscrito de 90° es la mitad del ángulo central de 180° (Utilizando el «Teorema del ángulo en el centro» anterior) |
 |
Otra buena razón Por qué funciona
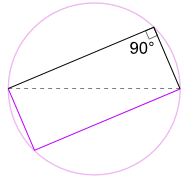
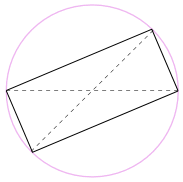
También podríamos rotar la forma alrededor ¡180° para hacer un rectángulo!
Es un rectángulo, porque todos los lados son paralelos, y ambas diagonales son iguales.
Y por lo tanto sus ángulos internos son todos ángulos rectos (90°).
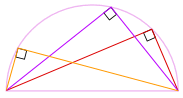
¡Así que ahí vamos! No importa dónde esté ese ángulo en la circunferencia, siempre es de 90 °
Ejemplo: ¿Cuál es el tamaño del ángulo BAC?
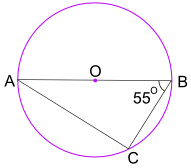
El Ángulo en el Teorema del Semicírculo nos dice que el ángulo ACB = 90 °
Ahora use ángulos de un triángulo agregue a 180° para encontrar el Ángulo BAC:
Encontrar el centro de un círculo
Podemos usar esta idea para encontrar el centro de un círculo:
- dibujar un ángulo recto desde cualquier lugar de la circunferencia del círculo, luego dibuja el diámetro donde las dos patas golpean el círculo
- haz eso de nuevo, pero para un diámetro diferente
¡Donde los diámetros se cruzan es el centro!
Cuadrilátero Cíclico
|
Un «Cíclica» Cuadrilátero tiene cada vértice sobre la circunferencia de un círculo: |
 |
|
Un Cuadrilátero Cíclico de ángulos opuestos añadir a 180°:
|
 |
Ejemplo: ¿Cuál es el tamaño de Ángulo WXY?
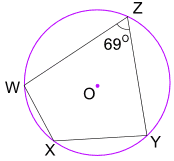
Opposite angles of a cyclic quadrilateral add to 180°

