Esta sección cubre:

• Introducción a las Funciones por Partes
• Evaluar Funciones por Partes
• Graficar Funciones por Partes
• Cómo Saber si una Función por Partes es Continua o No Continua
• Obtener Ecuaciones de Gráficos de Funciones por Partes
• Valor Absoluto como una Función por Partes
• Transformaciones de Funciones por partes
• Problemas verbales de función por partes
• Más práctica

Las funciones por partes (o funciones por partes) son justo lo que se llaman: piezas de diferentes funciones (subfunciones) en un gráfico. La forma más fácil de pensarlas es dibujando más de una función en un gráfico, y simplemente borrando partes de las funciones donde se supone que no deben estar (a lo largo de las \(x\)’s); se definen de manera diferente para diferentes intervalos de \(x\). \(y\) se define de manera diferente para diferentes valores de\ (x\); usamos\ (x\) para buscar en qué intervalo está, para que podamos averiguar qué se supone que es\ (y\).

Tenga en cuenta que hay un ejemplo del inverso de una función por partes aquí en la sección Inversos de funciones.

Here’s an example and graph:

Piecewise Function

Graph

\(\displaystyle f\left( x \right)=\left\{ \begin{align}2x+8\,\,\,\,\,&\text{ if }x\le -2\\{{x}^{2}}\,\,\,\,\,\,\,\text{ }\,&\text{ if }x>-2\end{align} \right.\) (Hay otras formas de mostrar esto, como usar un «for» en lugar de un «if», y usar comas o puntos y comas en lugar del «if».) Dominio: \(\mathbb{R},\,\,\,\text{o}\,\,\left( {-\infty ,\infty } \right)\) Gama: \(\mathbb{R},\,\,\,\text{o}\,\,\left( {-\infty ,\infty } \right)\)

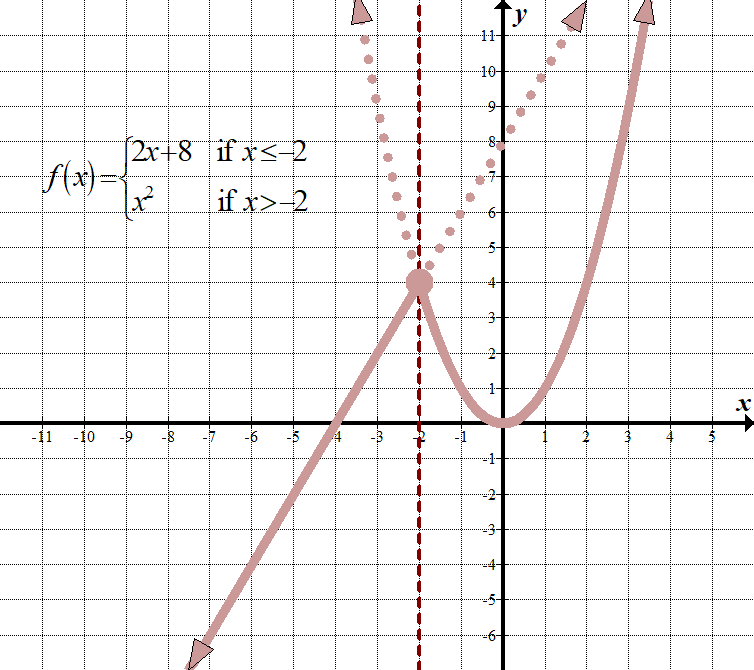Lo que esto significa es que cada \(x\) menor o igual a -2, tenemos la gráfica de la línea de \(2x+8\), como si fuera la única función en el gráfico. Para cada valor \(x\) mayor que -2, necesitamos graficar \({{x}^{2}}\), como si fuera la única función en el gráfico. Entonces tenemos que» deshacernos » de las partes que no necesitamos. Recuerde que todavía usamos el origen como punto de referencia para ambos gráficos.

¿Ves cómo la línea vertical \(x=-2\) actúa como una línea de «frontera» entre los dos gráficos?

Tenga en cuenta que el punto \((-2,4)\) tiene un círculo cerrado. Técnicamente, solo debería pertenecer a la función \(2x+8\), ya que esa función tiene el signo menor o igual, pero como el punto también está en el gráfico \({{x}^{2}}\), podemos usar un círculo cerrado como si apareciera en ambas funciones. No está tan mal, ¿verdad?

Evaluación de funciones por partes

A veces, se le darán funciones por partes y se le pedirá que las evalúe; en otras palabras, encuentre los valores \(y\) cuando se le dé un valor \(x\). Hagamos esto para \(x = -6\) y \(x=4\) (sin usar el gráfico). Aquí es la función de nuevo:

\(\displaystyle f\left( x \right)=\left\{ \begin{align}2x+8\,\,\,\,\,&\text{ si }x\le -2\\{{x}^{2}}\,\,\,\,\,\,\,\texto{ }\,&\text{ si }x>-2\end{align} \right.\)

Primero queremos mirar las condiciones a la derecha, para ver dónde está nuestro \(x\). Cuando \(x = -6\), sabemos que es menor que -2, por lo que conectamos nuestro \(x\) a \(2x+8\) solamente. \(f(x)\) o \(y\) es \((2)(-6)+8=-4\). ¡Ni siquiera nos importa el \(\símbolo en negrita {{x}^{2}}\)! Es así de fácil. También puedes ver que lo hicimos correctamente usando el gráfico de arriba.

Ahora prueba \(x = 4\). Miramos a la derecha primero, y ver que nuestro \(x\) es mayor que -2, así que enchufar en la \({{x}^{2}}\). (Solo podemos ignorar el \(2x + 8\) esta vez.) \(f(x)\) o \(y\) es \({{4}^{2}}=16\).

Graficar funciones por partes

Probablemente se le pedirá que grafique funciones por partes. A veces, los gráficos contendrán funciones que no son continuas o discontinuas, lo que significa que debe recoger su lápiz en el centro del gráfico cuando lo está dibujando (¡como un salto!). Funciones continuas significa que usted nunca tendrá que recoger su lápiz si se dibuja de izquierda a derecha.

Y recuerde que los gráficos son funciones verdaderas solo si pasan la Prueba de Línea Vertical.

Dibujemos estas funciones por partes y determinemos si son continuas o no continuas. Observe cómo dibujamos cada función como si fuera la única, y luego «borramos» las partes que no son necesarias. También obtendremos el Dominio y el Rango como lo hicimos aquí en la sección de Funciones Algebraicas.

Piecewise Function	Graph
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-2x+8\,\,\,\,\,\,\text{if }x\le 4\\\frac{1}{2}x-2\,\,\,\,\,\,\,\,\,\text{if }x>4\end{array} \right.\) Continuous Domain: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) Range: \(\left( {0,\infty } \right)\)
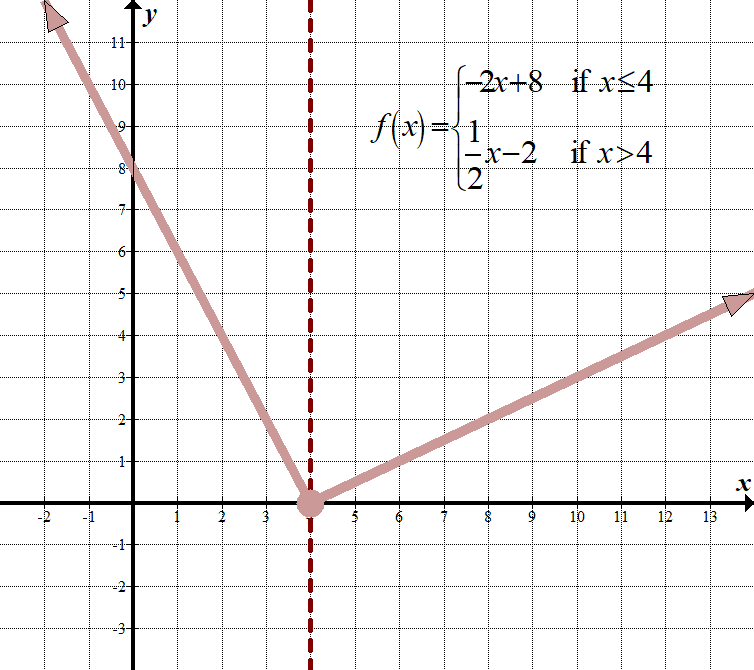\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\,\text{if }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1}\le x<4\\x-5\,\,\,\,\,\,\,\,\,\text{if }x\ge 4\end{array} \right.\) Non-Continuous Domain: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) Range: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\)

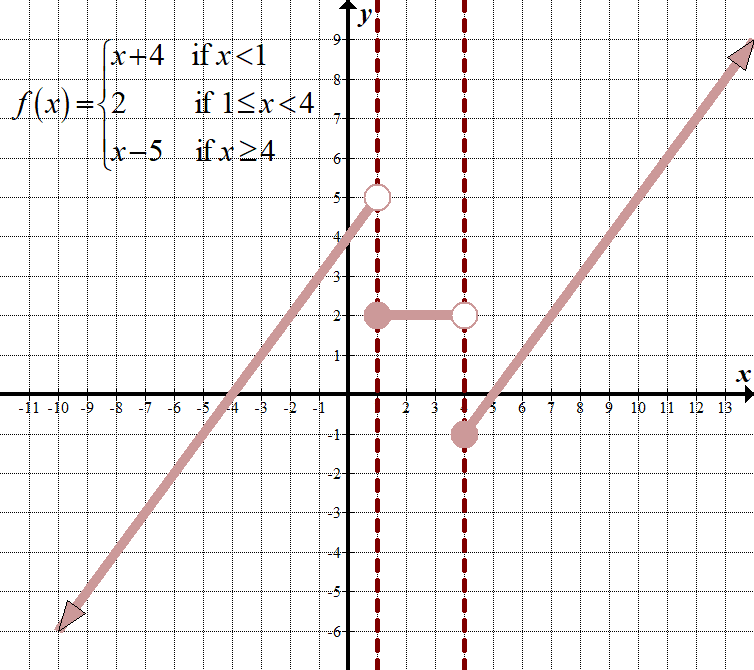We can actually put piecewise functions in the graphing calculator:

Piecewise Function Screens

Steps and Notes

Enter the piecewise function on three lines: he Aquí la gráfica:

poner los trozos de la función \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\,\text{si }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{si 1 }\le x<4\\-5+x\,\,\,\,\,\text{si }x\ge 4\end{array} \right.\ ) en la calculadora, puede ingresar la función en tres líneas dividiendo la función en cada intervalo por una «desigualdad de prueba» de ese intervalo (¡y vea los paréntesis!). La razón dividimos por los intervalos o las desigualdades, es porque la calculadora devolverá un 1 si la desigualdad (como \(x<1\)) es verdadera; por ejemplo, \((x+4)\) acaba de terminar \((x+4)/(1)\) cuando \(x<1\). Cuando \(x \ ge 1\), estamos dividiendo por 0, por lo que no se dibujará nada. Esto es lo que podemos poner en la calculadora: \(\displaystyle \begin{array}{l}{{Y}_{1}}=\left( {x+4} \derecho)/\left( {x<1} \derecho)\\{{Y}_{2}}=\left( 2 \derecho)/\left( {x\ge 1\text{ y }x<4} \derecho)\\{{Y}_{3}}=\left( {-5+x} \derecho)/\left( {x\ge 4} \derecho)\end{array}\) (tenga en cuenta que también puede introducir esto en una línea multiplicando las condiciones en lugar de dividir, y el uso de signos más entre cada una de las tres funciones/intervalos de: \(\displaystyle {{Y}_{1}}=\left( {x+4} \derecho)\left( {x<1} \derecho)+\left( 2 \derecho)\left( {x\ge 1\text{ y }x<4} \derecho)+\left( {-5+x} \derecho)\left( {x\ge 4} \right)\).) Aquí están las pulsaciones de teclas para usar tres líneas. Tenga en cuenta que utiliza 2nd MATH (PRUEBA) para llegar a la pantalla que tiene \(\le \), \(\ge \), y así sucesivamente. Por ejemplo, 2nd MATH 6 te da \(\le \). Use 2da MATEMÁTICA (PRUEBA), derecha a LÓGICA, luego 1, para el «y» en \({{Y}_{2}}\).

Cómo saber si la función por partes es Continua o No Continua

Para saber si un gráfico por partes es continuo o continuo, puedes mirar los puntos límite y ver si el punto \(y\) es el mismo en cada uno de ellos. (Si las \(y\) fueran diferentes, ¡habría un «salto» en el gráfico!)

Probemos esto para las funciones que usamos anteriormente:

Piecewise Function	Check Boundary Points
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-2x+8\,\,\,\,\,\,\,\text{if }x\le 4\\\frac{1}{2}x-2\,\,\,\,\,\,\,\,\,\,\text{if }x>4\end{array} \right.\)	Let’s check \(x=4\) in both parts of the function, since 4 is the «boundary point”: \(\begin{array}{l}-2(4)+8=0\\\,\,\,\frac{1}{2}(4)-2=0\end{array}\) Desde \(0=0\), este trozos de la función es continua.
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\,\,\,\,\,\text{si }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{si 1 }\le x<4\\-5+x\,\,\,\,\,\,\,\,\,\text{si }x\ge 4\end{array} \right.\)	Revisemos las dos primeras partes de la función. Nota en la segunda parte, \(y\) es siempre 2: \(\begin{array} {l}1+4=5\\\,\,\,\,\,\,\,\,\,2=2\end{array}\) Desde \(5\ne 2\), podemos detenernos aquí y observar que esta función por partes no es continua. Si los \(y\) fueran iguales, tendríamos que ir uno para comprobar el siguiente punto límite en \(x=4\).

Obtención de ecuaciones a partir de gráficos de funciones por partes

Se le puede pedir que escriba una función por partes, dada una gráfica. Ahora que sabemos de qué se tratan las funciones por partes, ¡no es tan malo!

Para revisar cómo obtener ecuaciones a partir de gráficos lineales, consulte Obtención de Ecuaciones de una Recta y de cuadráticas, consulte Encontrar una Ecuación cuadrática a partir de Puntos o de un Gráfico.

Aquí están los gráficos, con explicaciones sobre cómo derivar sus ecuaciones por partes:

Piecewise Function Graph	Procedure to get Function
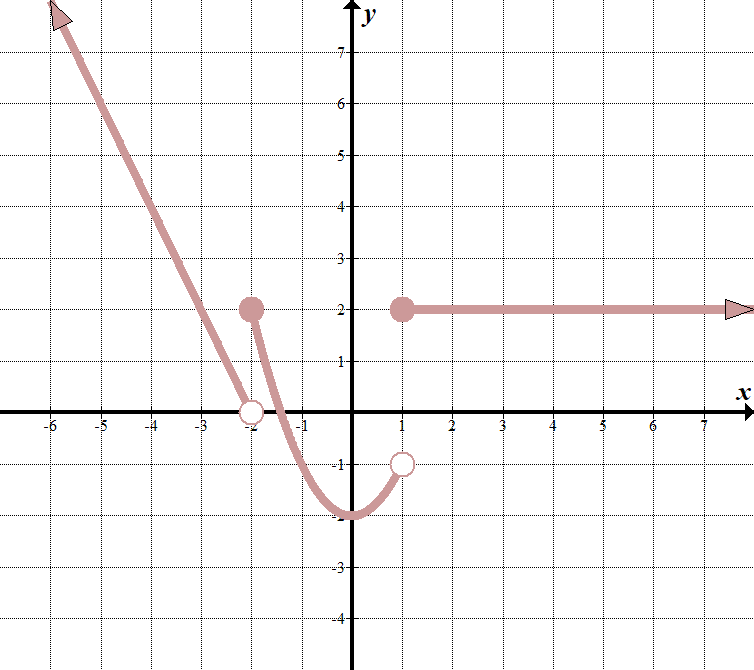	We see that our «boundary lines” are at \(x=-2\) and \(x=1\). We know that our function will look something like this (notice open and closed endpoints): \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }……\,\,\,\,\,\,\,\,\text{si }x<-2\\\text{ }……\,\,\,\,\,\,\,\,\text{si }-\text{2 }\le x<1\\\text{ }……\,\,\,\,\,\,\,\,\text{si }x\ge 1\end{array} \right.\) Podemos elegir dos puntos \((-2,0)\) y \((-3,2)\) en la línea de más a la izquierda para obtener la ecuación \(y=-2x-4\). La función intermedia es \(y = {{x}^{2}}-2\), y la función más a la derecha es solo la línea horizontal \(y = 2\). Por lo tanto, la función por partes es: \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-2x-4\,\,\,\,\,\,\,\text{si }x<-2\\\text{ }{{x}^{2}}-2\,\,\,\,\,\,\,\,\,\,\text{si }-\text{2}\le x<1\\\text{ 2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{si }x\ge 1\end{array} \right.\)
	vemos que nuestra «línea divisoria» es \(x=5\). Dado que las líneas se encuentran en \((5,4)\), no importa dónde pongamos el signo \(\le \) o \(\ge \) ; simplemente no podemos ponerlo en ambos lugares, o no sería una función. Tenemos hasta el momento: \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }……\,\,\,\,\,\,\,\,\,\text{si }x<5\\\text{ }……\,\,\,\,\,\,\,\,\,\text{si }x\ge 5\end{array} \right.\) De nuevo, tenemos que mirar cada línea por separado para determinar sus ecuaciones. Podemos tomar 2 puntos de cada línea para obtenerlos, o derivar de pendientes e intercepciones \(y\); la función por partes es: \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\frac{6}{5}x-2\,\,\,\,\,\,\,\text{si }x<5\\\frac{2}{5}x+2\,\,\,\,\,\,\,\text{si }x\ge 5\end{array} \right.\)

Valor absoluto como una función por partes

Podemos escribir funciones de valor absoluto como funciones por partes – ¡es realmente genial! Es posible que desee revisar la Resolución de Ecuaciones de Valor Absoluto y Desigualdades antes de continuar con este tema.

supongamos que tenemos la función \(f\left( x \right)=\left| x \right|\). De lo que aprendimos anteriormente, sabemos que cuando \(x\) es positivo, ya que estamos tomando el valor absoluto, seguirá siendo \(x\). Pero cuando \(x\) es negativo, cuando tomamos el valor absoluto, tenemos que tomar lo opuesto (negarlo), ya que el valor absoluto tiene que ser positivo. Sentido? Así, por ejemplo, si tuviéramos \(/5/\), simplemente tomamos lo que está dentro del signo absoluto, ya que es positivo. Pero para \(/-5/\), tenemos que tomar el opuesto (negativo) de lo que está dentro del valor absoluto para hacerlo \(\displaystyle 5\,\,\,(-\,-5=5)\).

Esto significa que podemos escribir esta función de valor absoluto como una función por partes. Observe que podemos obtener el» punto de inflexión «o el» punto límite » estableciendo lo que esté dentro del valor absoluto en 0. Luego usaremos la función original o negaremos la función, dependiendo del signo de la función (sin el valor absoluto) en ese intervalo.

Por ejemplo, podemos escribir \(\displaystyle \left| x \right|\text{ }=\left\{ \begin{array}{l}x\,\,\,\,\,\,\,\,\,\text{si }x\ge 0\\-x\,\,\,\,\,\text{si }x<0\end{array} \right.\). También tenga en cuenta que, si la función es continua (no hay «salto») en el punto límite, no importa dónde pongamos los signos «menor o igual a» (o «mayor o igual a»), ¡siempre y cuando no los repitamos! No podemos repetirlas porque, teóricamente, no podemos tener dos valores de \(y\) para el mismo \(x\), o no tendríamos una función.

Here are more examples, with explanations. (You might want to review Quadratic Inequalities for the second example below):

Absolute Value Function	Method to get Piecewise Function
\(g\left( x \right)=\left| {2x+3} \right|\)	Let’s first find the «boundary line”. Hacemos esto estableciendo lo que está dentro del valor absoluto en 0, y luego resolviendo para \(\boldsymbol{x}\). Cuando \(2x + 3 \ ge 0\), obtenemos \(\displaystyle x\ge -\frac{3}{2}\) (en realidad, podemos mantener el \(\ge\) cuando resolvemos). Cuando \(2x + 3\) es positivo, simplemente lo tomamos «tal cual», pero si es negativo, tenemos que negarlo todo. Por lo tanto, la función por partes es: \(\displaystyle \left| {2x+3} \derecho|=\left\{ \begin{array}{l}2x+3\,\,\,\,\,\,\,\,\,\text{si }x\ge -\frac{3}{2}\text{ }\\-2x-3\,\,\,\,\,\text{si }x<\frac{3}{2}\end{array} \right.\) Pruébalo – ¡funciona!
\(f\left( x \right)=\left| {{{x}^{2}}-4} \right|\)	Vamos a encontrar primero la «línea límite(s)»; hemos establecido lo que está dentro del valor absoluto a 0. Cuando \({{x}^{2}}-4 \ ge 0\), obtenemos \(x \ le -2\) o \(x \ ge 2\) (¡prueba algunos números!). Cuando \({{x}^{2}}-4\) es positivo, simplemente lo tomamos «tal cual», pero si es negativo, tenemos que negarlo. La función definida a tramos es la siguiente: \(\displaystyle \left| {{{x}^{2}}-4} \derecho|=\left\{ \begin{array}{l}{{x}^{2}}-4\,\,\,\,\,\text{si }x\le -2\\4-{{x}^{2}}\,\,\,\,\,\text{si }-2<x<2\\{{x}^{2}}-4\,\,\,\,\,\text{si }x\ge 2\text{ }\end{array} \right.\) o \(\displaystyle \left| {{{x}^{2}}-4} \derecho|=\left\{ \begin{array}{l}{{x}^{2}}-4\,\,\,\,\,\,\text{si }x\le -2\text{ }\,\,\text{o}\,\,\text{ }x\ge 2\\4-{{x}^{2}}\,\,\,\,\,\,\,\text{si }-2<x<2\end{array} \right.\) de Nuevo (ya que la función es continua), realmente no importa de donde tenemos el \(\le \) y \(\ge \) (en oposición a \(<\) y \(>\)), siempre que no se repita.
\(f\left( x \right)=2x+\left| {x+2} \right|\)	Este es un poco más complicado, ya que tenemos una \(x\) dentro y fuera del valor absoluto. Para la «línea de límite», solo usamos lo que está dentro del valor absoluto. Cuando \(x + 2 \ ge 0\), obtenemos \(x\ge -2\). Pero para la función por partes, tenemos que usar toda la función, incluida la parte que está fuera del valor absoluto. Por lo tanto, la función por partes es: \(\displaystyle 2x+\left| {x+2} \right|=\left\{ \begin{array}{l}2x+x+2\,\,\,\,\,\text{si }x\ge -2\\2x-x-2\,\,\,\,\,\text{si }x<-2\end{array} \right.\) Vamos a simplificar: \(\displaystyle 2x+\left| {x+2} \right|=\left\{ \begin{array}{l}3x+2\,\,\,\,\,\,\,\text{si }x\ge -2\\x-2\,\,\,\,\,\,\,\,\,\,\text{si }x<-2\end{array} \right.\) Pruebe algunos valores inferiores y excelentes entonces -2; ¡deberían funcionar!
\(g\left( x \right)=\left| {{{x}^{2}}-4x-5} \right|\)	Esta es la mejor opción resuelto con un signo gráfico, ya tenemos una ecuación cuadrática y necesitamos saber donde la función es positiva y negativa. Primero, factoriza la cuadrática dentro de la función de valor absoluto a \(\left ({x-5} \right)\left ({x+1} \right)\). Luego use un gráfico de signos para ver dónde los factores son positivos y negativos, y recuerde que cuando los factores son positivos, usamos la función «tal cual», y donde los factores son negativos, negamos la función: \(\displaystyle \left| {{{x}^{2}}-4x-5} \derecho|=\left\{ \begin{array}{l}{{x}^{2}}-4x-5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{si }x\le -1\,\,\,\,\text{o}\,\,\,\,x\ge 5\\-\left( {{{x}^{2}}-4x-5} \derecho)\,\,\,\,\text{si }-1<x<5\text{ }\end{array} \right.\)
\(\displaystyle g\left( x \right)=\frac{{\left| {x+2} \right|}}{{x+2}}\)	Esta es una función racional, ya que hay una variable en el denominador. Cuando \(x + 2 \ ge 0\), obtenemos \(\displaystyle x\ge -2\). Cuando \(x+2\) es positiva, sólo se tarda «como es», pero si es negativo, tenemos que negar lo que está en el valor absoluto: \(\displaystyle \frac{{\left| {x+2} \right|}}{{x+2}}=\left\{ \begin{array}{l}\frac{{x+2}}{{x+2}}\,\,\,\,\,\,\,\,\,\text{si }x\ge -2\\\frac{{-x-2}}{{x+2}}\,\,\,\,\,\,\text{si }x<-2\end{array} \right.\). Pero tenemos que tener cuidado, ya que \(x \ ne 2\) (restricción de dominio: el denominador sería 0). Por lo tanto, la función por partes es: \(\displaystyle \frac{{\left| {x+2} \right|}}{{x+2}}=\left\{ \begin{array}{l}1\,\,\,\,\,\,\,\,\,\,\text{si }x>-2\\-1\,\,\,\,\,\,\text{si }x<-2\end{array} \right.\).

También se le puede pedir que tome un gráfico de valor absoluto y lo escriba como una función por partes:

Absolute Value Graph	Method to get Piecewise Function
	We see that our «boundary line” is at \(x=0\), so what’s inside the absolute value sign must be \(x\) or a factor of \(x\). (Esto se debe a que para obtener la línea de límite con una función de valor absoluto, establecemos lo que está dentro del valor absoluto en 0, y resolvemos para \(x\)). Cuando \(x>0\), podemos ver que la ecuación de la línea es \(y=2x-2\). Cuando \(x< 0\), la ecuación es \(y=2x-2\). Podemos escribir esto como una función definida a tramos: \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}2x-2\,\,\,\,\,\,\,\text{si }x>0\\-2x-2\,\,\,\text{si }x\le 0\end{array} \right.\) También podemos escribir esto como una función de valor absoluto transformado: \(y=2\left| x \right|-2\) o \(y=\left| {2x} \right|-2\) (dado que 2 es positivo, puede estar dentro o fuera de \(\left| {\,\,} \right|\)). (Esto tiene sentido ya que cuando lo que está dentro de \(\left| {\,\,} \right|\) es \(> 0\), usamos la función regular \(y=2x-2\), y cuando lo que está dentro de \(< 0\), negamos la parte de valor absoluto para hacerla \(y=-\left( {2x} \right)-2\)).
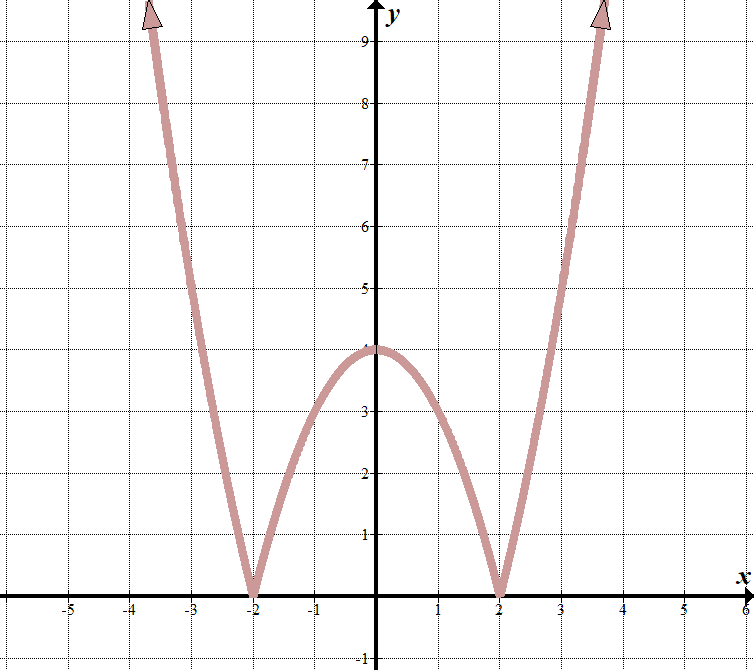	vemos que nuestras «líneas límite» son en \(x=2\) y \(x=-2\), así que lo que está dentro del valor absoluto signo debe tener factores de \(x-2\) y \(x+2\). Cuando \(x< -2\) o \(x> 2\), podemos ver que el gráfico se parece a la parte normal del gráfico \(y = {{x}^{2}}-4\). (¡Descubrí esto conociendo los factores y adivinando bien!) Cuando \(-2<x<2\), la ecuación se invierte, o negación (se volcó a la de \(x\)-eje). Podemos escribir esto como una función definida a tramos: \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}{{x}^{2}}-4\,\,\,\,\,\,\,\,\,\text{si }x<-2\text{ o }x>2\\-{{x}^{2}}\text{+ 4}\,\,\,\,\,\,\text{si }-2\le x\le 2\end{array} \right.\) Podemos ver que esto comenzó con una función cuadrática transformada \(y={{x}^{2}}-4\) con un valor absoluto a su alrededor, ya que todos los valores \(y\) son positivos: \(y=\left| {{{x}^{2}}-4} \right|\).
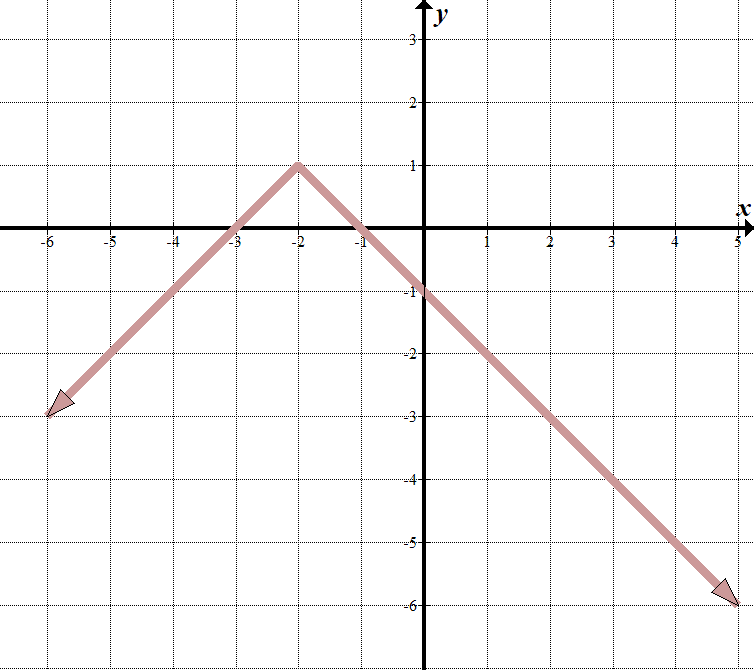	vemos que nuestra «línea divisoria» es \(x=-2\), así que lo que está dentro del valor absoluto signo debe ser \(x+2\). Cuando \(x>-2\), podemos ver que la ecuación de la línea es \(y=-x-1\). Cuando \(x<-2\), la línea es \(y=x+3\). Podemos escribir esto como una función definida a tramos: \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-x-1\,\,\,\,\,\,\text{si }x>-2\\x+3\,\,\,\,\,\,\,\,\,\,\text{si }x\le -2\end{array} \right.\) Probablemente sea más fácil escribir esto como una función de valor absoluto transformado. Podemos ver que la función de valor absoluto principal se voltea verticalmente, se mueve a la izquierda 2 y hacia arriba 1. Nuestra ecuación de valor absoluto es \(y=- \ left / {x + 2} \right|\,\,+\,\,1\). Esto es lo mismo que la función por partes anterior. Pruébalo, funciona!

Transformaciones de funciones por partes

Hagamos una transformación de una función por partes. Aprendimos acerca de las Funciones Principales y sus Transformaciones aquí en la sección de Gráficos y Transformaciones Principales. Probablemente querrás leer esta sección primero, antes de intentar una transformación por partes.

Transformemos la siguiente función por partes volteada alrededor del eje \(x\), estirada verticalmente por un factor de 2 unidades, 1 unidad a la derecha y 3 unidades hacia arriba.

vamos a sacar \(-2f\left( x-1 \derecho)+3\), donde:

\(\displaystyle f\left( x \right)=\left\{ \begin{align}x+4\,\,\,\,\,\,\,\,&\text{ si }x<&\text{ si 1 }\le x<4\\x-5\,\,\,\,\,\,\,\,&\text{ si }x\ge 4\end{align} \right.\)

Asegurémonos de usar los puntos «límite» cuando rellenemos el gráfico en t para la transformación. Recuerde que las transformaciones dentro de los paréntesis se hacen a la \(x\) (haciendo la matemática opuesta), y fuera se hacen a la \(y\). Para crear un gráfico en t, como se muestra en la tabla a continuación, podemos usar puntos clave, incluidos dos puntos en cada una de las «líneas de límite».

Tenga en cuenta que debido a que esta transformación es complicada, podemos idear una nueva función por partes transformando las 3 «piezas» y también transformando las «\(x\)»donde están los puntos límite (agregando 1, o yendo a la derecha 1), ya que hacemos las matemáticas opuestas para las «\(x\)». Para obtener las nuevas funciones en cada intervalo, podemos sustituir » \(x-1\) «por» \(x\) » en la ecuación original, multiplicar por -2 y luego agregar 3. Por ejemplo, \(\displaystyle-2f \ left ({x-1} \right)+3=-2\left+3=-2\left ({x+3} \right)+3=-2x-3\).

\(\displaystyle -2f\left( {x-1} \derecho)+3=\left\{ \begin{array}{l}-2\left( {\left( {x-1} \derecho)+4} \derecho)+3=-2x-3,\,\,\,\,\text{ si }x-1<1\,\,\,\left( {x<2} \derecho)\\-2\left( 2 \derecho)+3=-1,\,\,\,\,\text{ si }\,\text{ 2 }\le x<5\\-2\left( {\left( {x-1} \derecho)-5} \derecho)+3=-2x+15,\,\,\,\,\text{ si }x\ge 5\end{array} \right.\)

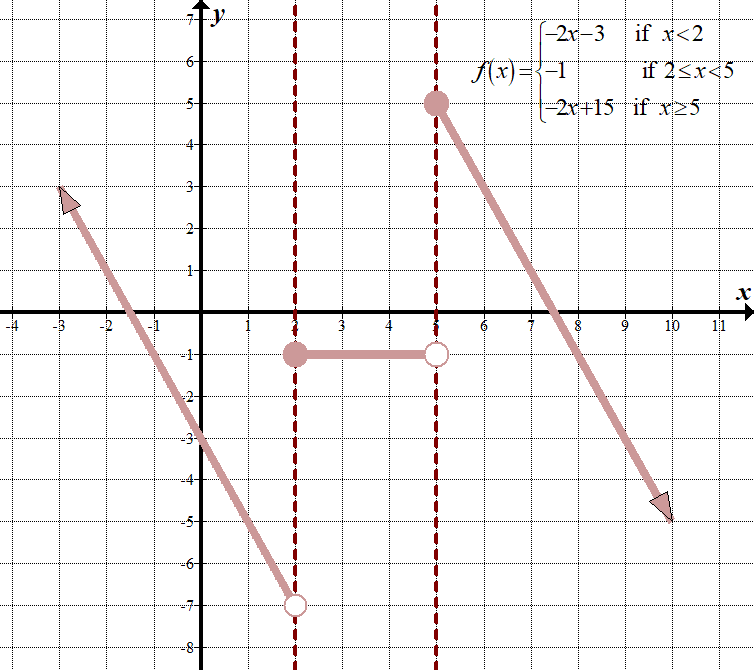
Aquí están los gráficos «antes» y «después», incluido el gráfico en t:

Piecewise Parent Function	T-chart	Transformation of Function
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\text{if }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1 }\le x<4\\x-5\,\,\,\,\,\,\,\,\text{if }x\ge 4\end{array} \right.\)	x + 1 x y –2y+3 1 0 4 –5 2 1 5 –7 2 1 2 –1 5 4 2 –1 5 4 –1 5 8 7 2 –1	\(\displaystyle -2f\left( {x-1} \right)+3=\left\{ \begin{array}{l}-2x-3\,\,\,\,\,\,\,\,\,\text{if }x<2\\-1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 2}\le x<5\\-2x+15\,\,\,\,\,\,\text{if }x\ge 5\end{array} \right.\)

Piecewise Function Word Problems

Problem:

Su peluquero de perros favorito cobra de acuerdo con el peso de su perro. Si su perro pesa 15 libras o menos, el peluquero cobra 3 35. Si su perro pesa entre 15 y 40 libras, cobra 4 40. Si su perro pesa más de 40 libras, cobra 4 40, más 2 2 adicionales por cada libra.

(a) Escriba una función por partes que describa lo que cobra su peluquero de perros.

(b) Grafique la función.

(c) ¿Qué cobraría el peluquero si su lindo perro pesa 60 libras?

Solución:

(a) Vemos que los «puntos límite» son 15 y 40, ya que estos son los pesos donde cambian los precios. Dado que tenemos dos puntos de frontera, tendremos tres ecuaciones en nuestra función por partes. Tenemos que empezar en 0, ya que los perros tienen que pesar más de 0 libras:

\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }……\,\,\,\,\,\,\,\,\,\text{si }0<x\le 15\\\text{ }……\,\,\,\,\,\,\,\,\,\text{si }15<x\le 40\\\text{ }……\,\,\,\,\,\,\,\,\,\text{si }x>40\end{array} \right.\)

Estamos buscando las » respuestas «(cuánto cuesta el aseo) a las» preguntas » (cuánto pesa el perro) para los tres rangos de precios. Los dos primeros son solo tarifas fijas ($35 y 4 40, respectivamente). La última ecuación es un poco más complicada; el peluquero cobra 4 40 más 2 2 por cada libra de más de 40. Probemos números reales: si su perro pesa 60 libras, cobrará 4 40 más 2 2 veces \(20 (60-40)\). Vamos a convertir esto en una ecuación: \(40+2(x–40)\), que se simplifica a \(2x–40\) (ver cómo 2 es la pendiente?).

Toda la función por partes es:

\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }35\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{si }0<x\le 15\\\text{ }40\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{si }15<x\le 40\\\text{ }40+2\left( {x-40} \derecho)\,\,\,\,\,\,\text{si }x>40\end{array} \right.\) o \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }35\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{si }0<x\le 15\\\text{ }40\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{si }15<x\le 40\\\text{ }2x-40\,\,\,\,\,\,\,\text{si }x>40\end{array} \right.\)

(b) Hagamos un gráfico:Tenga en cuenta que esta ecuación por partes no es continua. También tenga en cuenta que un dominio razonable para este problema podría ser \(\left ({0,200} \right]\) (dado que los perros no pesan más de 200 libras!) y un rango razonable podría ser \(\left\cup \left\).

(c) Si su perro pesa 60 libras, podemos usar el gráfico o la función para ver que tendría que pagar $80. Whoa! ¡Eso cuesta más que un corte de pelo humano (al menos mis cortes de pelo)!

Problema:

Planeas vender camisetas de She Love Math para recaudar fondos. La compañía de camisetas al por mayor le cobra 1 10 por camisa por las primeras 75 camisas. Después de comprar las primeras 75 camisas hasta 150, la compañía bajará su precio a 7 7.50 por camisa. Después de comprar 150 camisas, el precio disminuirá a 5 5 por camisa. Escriba una función que modele esta situación.

Solución:

Vemos que los» puntos límite » son 75 y 150, ya que estos son el número de camisetas compradas donde cambian los precios. Dado que tenemos dos puntos de frontera, tendremos tres ecuaciones en nuestra función por partes. Comenzaremos con \(x\ge 1\), ya que asumimos que se compró al menos una camisa. Nota en este problema, el número de camisetas compradas (\(x\)), o el dominio, debe ser un entero, pero esta restricción no debería afectar el resultado del problema.

\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }……\text{ si }1\le x\le el 75\\\text{ }……\text{ si }75<x\le 150\\\text{ }……\text{ si }x>150\end{array} \right.\)

Estamos buscando las » respuestas «(costo total de las camisetas) a las» preguntas » (cuántas se compran) para los tres rangos de precios.

Para un máximo de 75 camisas incluidas, el precio es de $10, por lo que el precio total sería \(10x\). Para más de 75 camisas, pero hasta 100, el costo es de 7 7.50, pero las primeras 75 camisetas aún costarán 1 10 por camisa. La segunda función incluye los $750 pasó de la primera camisetas de 75 (75 veces $10), y también incluye $7.50 veces el número de camisetas más del 75, que sería \((x-75)\). Por ejemplo, si compraras 80 camisas, tendrías que gastar \(\$10 \ veces 75= \ $750\), más \(\$7,50\veces 5\,\) (80 – 75) para las camisas después de la camiseta 75.

Del mismo modo, para más de 150 camisas, todavía pagaríamos el precio de $10 hasta 75 camisas, los shirts 7.precio de 50 por 76 a 150 camisas (75 camisas más), y luego 5 5 por camisa por el número de camisas compradas de más de 150. Pagaremos \(10(75)+7.50(75)+5(x-150)\) para camisas \(x\). ¡Pon números y pruébalo!

La función definida a tramos es la siguiente:

\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }10x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{si }1\le x\le el 75\\\text{ }7.5 x\text{ }+\text{ }187.5\,\,\,\,\,\texto{7}5<x\le 150\\\text{ }5x+562.5\,\,\,\,\,\,\,\,\,\,\text{ if} x> 150 \ end{array} \ right.\) o \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }10x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{si }1\le x\le el 75\\\text{ }7.5 x\text{ }+\text{ }187.5\,\,\,\,\,\texto{7}5<x\le 150\\\text{ }5x+562.5\,\,\,\,\,\,\,\,\,\,\,\text{si }x>150\end{array} \right.\)

Problema:

Un servicio de autobús cuesta 5 50 por las primeras 400 millas, y cada 300 millas adicionales (o una fracción de las mismas) agrega $10 a la tarifa.

Utilice una función por partes para representar la tarifa del autobús en términos de la distancia en millas.

Solución:

Este es en realidad un problema complicado, pero pensemos primero en el «punto límite», que es 400. Es bastante sencillo cuando el viaje es de menos de 400 millas; el costo es de $50.

Para más de 400 millas, tenemos que restar las primeras 400 millas (pero recuerde incluir los primeros 5 50), dividir el número de millas restantes por 300 millas (y redondear, si hay una cantidad fraccionada), y multiplicar eso por $10.

La parte difícil es cuando «redondeamos» una parte de las próximas 300 millas. Podemos usar una función «ceiling» (designada por \(\left\lceil {} \right\rceil \)); esta función da el número entero mínimo que es mayor o igual a su entrada; por ejemplo, el techo de 3.5 y 4 es 4.

por Lo tanto, esto es lo que tenemos:

\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }50\text{ }\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{si }0\le x\le de 400\\\text{ }50+10\times \left\lceil {\frac{{x-400}}{{300}}} \a la derecha\rceil \text{ }\,\,\,\,\,\,\text{ si }x>400\end{array} \right.\)

¡Probémoslo! Si tenemos un viaje de 1500 millas, el costo sería \(\displaystyle 50+10 \ times \ left \ lceil {\frac{{1500-400}}{{300}}} \derecha\rceil \ text { } = 50 + 10 \ times 4 = \ 9 90\).

Problema:

¿Qué valor de \(\boldsymbol{a}\) haría que esta función por partes fuera continua?

\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}3{{x}^{2}}+4\,\,\,\,\,\text{ si }x<-2\\5x+\boldsymbol{un}\,\,\,\,\,\,\,\,\text{si }x\ge -2\end{array} \right.\)

Solución:

Para que la función por partes sea continua, en el punto límite (donde cambia la función), los dos valores \(y\) deben ser los mismos. Podemos enchufe -2 para \(x\) en dos de las funciones y asegúrese de que el \(y\)’s son el mismo

\(\begin{align}3{{x}^{2}}+4&=5x+a\\3{{\left( {-2} \derecho)}^{2}}+4&=5\left( {-2} \derecho)+a\\12+4&=-10+a\\a&=26\end{align}\)

Si \(a=26\), los trozos de la función es continua!

Aprenda estas reglas, y practique, practique, practique!

Más práctica: Use el widget Mathway a continuación para intentar escribir una función por partes. Haga clic en Enviar (la flecha azul a la derecha del problema) y haga clic en Escribir el Valor absoluto a trozos para ver la respuesta.

También puede escribir su propio problema, o haga clic en los tres puntos en la esquina superior derecha y haga clic en «Ejemplos» para profundizar por tema.

Si hace clic en Tap para ver los pasos, o haga clic Aquí, puede registrarse en Mathway para una prueba gratuita y luego actualizar a una suscripción de pago en cualquier momento (¡para resolver cualquier tipo de problema matemático!).

A Matrices y Resolver Sistemas con Matrices – ¡ya está listo!