Konigsberg es una ciudad en el río Preger, que en el siglo XVIII era una ciudad alemana, pero ahora es rusa. Dentro de la ciudad hay dos islas que están conectadas a las orillas con siete puentes(como se muestra a continuación).
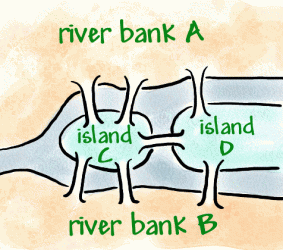
Se convirtió en una tradición tratar de caminar por la ciudad de una manera que solo cruzaba cada puente una vez, pero resultó ser un problema difícil. Leonhard Euler, un matemático suizo al servicio de la emperatriz rusa Catalina la Grande, se enteró del problema.En 1736 Euler demostró que el paseo no era posible. Esto se aprobó inventando una especie de diagrama llamado red, que se compone de vértices (puntos donde las líneas se encuentran) y arcos(líneas).
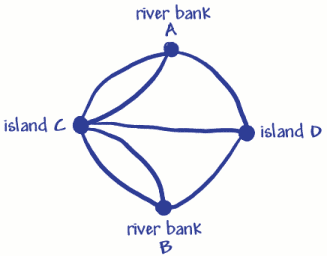
Usó cuatro puntos (vértices) para las dos orillas del río y las dos tierras. Estos han sido marcados A, B y C, D. Las siete líneas (arcos) son los siete puentes. Puede ver que 3 puentes (arcos)se unen a la orilla del río A, y 3 se unen a la orilla del río B. 5 puentes (arcos)se unen a la isla C, y 3 se unen a la isla D. Esto significa que todos los vértices tienen un número impar de arcos, por lo que se denominan vértices extraños. (Un vértice par tendría que tener un número par de arcos unidos a él).Recuerde que el problema era viajar por la ciudad cruzando cada puente solo una vez. En la red de Euler, esto significaba trazar sobre cada arco una sola vez, visitando todos los vértices. Euler demostró que no se podía hacer porque descubrió que para tener un vértice extraño tendrías que comenzar o terminar el viaje en ese vértice. (Piénsalo).Dado que solo puede haber un principio y un final, solo pueden haber dos vértices impares si vas a poder trazar sobre cada arco una sola vez. Dado que el problema del puente tiene 4 vértices impares, ¡no es posible hacerlo! ¿Qué sucede si no hay vértices impares? ¿Se puede rastrear esta red?
La invención de las redes comenzó un nuevo tipo de geometría calledTopology. La topología se utiliza ahora de muchas maneras, incluso para planificar y cartografiar redes ferroviarias. (Ahhh! Los trenes tenían que entrar….)