Orbitales atómicos
Un orbital es el refinamiento mecánico cuántico de la órbita de Bohr. En contraste con su concepto de una órbita circular simple con un radio fijo, los orbitales son regiones del espacio derivadas matemáticamente con diferentes probabilidades de tener un electrón.
Una forma de representar las distribuciones de probabilidad de electrones se ilustra en la Figura 6.5.2 para el orbital 1s del hidrógeno. Debido a que Ψ2 da la probabilidad de encontrar un electrón en un volumen de espacio dado (como un picómetro cúbico), una gráfica de Ψ2 versus distancia desde el núcleo (r) es una gráfica de la densidad de probabilidad. El orbital 1s es esféricamente simétrico, por lo que la probabilidad de encontrar un electrón 1s en un punto dado depende solo de su distancia del núcleo. La densidad de probabilidad es mayor en r = 0 (en el núcleo) y disminuye constantemente a medida que aumenta la distancia. En valores muy grandes de r, la densidad de probabilidad de electrones es muy pequeña pero no cero.
En contraste, podemos calcular la probabilidad radial (la probabilidad de encontrar un electrón 1s a una distancia r del núcleo) sumando las probabilidades de que un electrón esté en todos los puntos de una serie de x capas esféricas de radio r1, r2, r3,…, rx − 1, rx. En efecto, estamos dividiendo el átomo en capas concéntricas muy delgadas, como las capas de una cebolla (parte (a) de la Figura \(\pageIndex{1}\)), y calculando la probabilidad de encontrar un electrón en cada capa esférica. Recuerde que la densidad de probabilidad de electrones es mayor en r = 0 (parte (b) en la Figura \(\pageIndex{1}\)), por lo que la densidad de puntos es mayor para las capas esféricas más pequeñas en la parte (a) de la Figura \(\pageIndex{1}\). En contraste, el área de superficie de cada concha esférica es igual a 4nr2, que aumenta muy rápidamente con el aumento de r (parte (c) en la figura \(\pageIndex{1}\)). Debido a que el área de superficie de las capas esféricas aumenta más rápidamente con el aumento de r que la densidad de probabilidad de electrones disminuye, la gráfica de probabilidad radial tiene un máximo a una distancia particular (parte (d) en la Figura \(\pageIndex{1}\)). Lo más importante, cuando r es muy pequeña, el área de superficie de una capa esférica es tan pequeña que la probabilidad total de encontrar un electrón cerca del núcleo es muy baja; en el núcleo, la probabilidad de electrones desaparece (parte (d) en la Figura \(\pageIndex{1}\)).

Para el átomo de hidrógeno, el pico en la gráfica de probabilidad radial se produce en r = 0,529 Å (52,9 pm), que es exactamente el radio calculado por Bohr para la órbita n = 1. Por lo tanto, el radio más probable obtenido de la mecánica cuántica es idéntico al radio calculado por la mecánica clásica. En el modelo de Bohr, sin embargo, se suponía que el electrón estaba a esta distancia el 100% del tiempo, mientras que en el modelo de mecánica cuántica de Schrödinger, está a esta distancia solo una parte del tiempo. La diferencia entre los dos modelos es atribuible al comportamiento ondulatorio del electrón y al principio de incertidumbre de Heisenberg.
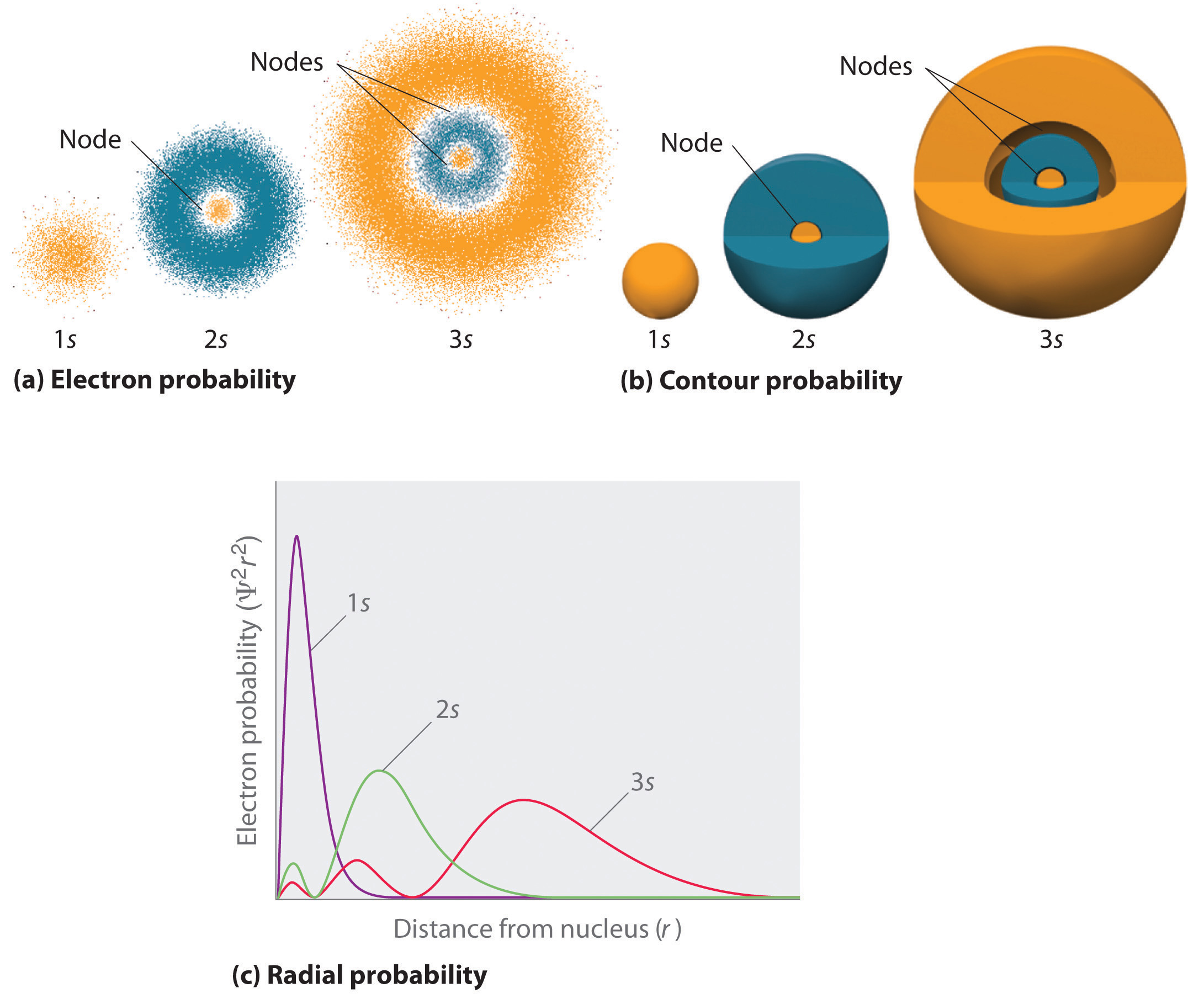
La figura \(\pageIndex{2}\) compara las densidades de probabilidad de electrones para los orbitales de hidrógeno 1s, 2s y 3s. Tenga en cuenta que los tres son esféricamente simétricos. Sin embargo, para los orbitales 2s y 3s (y para todos los demás orbitales s también), la densidad de probabilidad de electrones no se cae suavemente con el aumento de r. En su lugar, se observan una serie de mínimos y máximos en las gráficas de probabilidad radial (parte (c) en la Figura \(\pageIndex{2}\)). Los mínimos corresponden a nodos esféricos (regiones de probabilidad de electrones cero), que alternan con regiones esféricas de probabilidad de electrones distinta de cero.