Purplemath
In der Mathematik ist eine „Identität“ eine Gleichung, die immer wahr ist. Diese können „trivial“ wahr sein, wie „x = x“ oder nützlich wahr, wie der Satz des Pythagoras „a2 + b2 = c2“ für rechtwinklige Dreiecke. Es gibt viele trigonometrische Identitäten, aber die folgenden sind diejenigen, die Sie am wahrscheinlichsten sehen und verwenden.
Basic & Pythagorean, Angle-Sum & -Difference, Double-Angle, Half-Angle, Sum, Product
Content Continues Below
MathHelp.com
Need a custom math course?
K12 | College | Test Prep

Grundlegende und Pythagoreische Identitäten
Beachten Sie, dass ein „co- (etwas)“ -Triggerverhältnis immer der Kehrwert eines „Nicht-Co“ -Verhältnisses ist. Sie können diese Tatsache verwenden, um gerade zu halten, dass cosecant mit Sinus und Sekante mit Cosinus geht.
Die folgenden (insbesondere die erste der drei folgenden) werden als „pythagoreische“ Identitäten bezeichnet.
sin2(t) + cos2(t) = 1
tan2(t) + 1 = sec2(t)
1 + cot2(t) = csc2(t)
Advertisement
Beachten Sie, dass die drei Identitäten vor allem die Quadrierung und die Zahl 1 beinhalten. Sie können die Pythagoreisch-Yom-Beziehung deutlich sehen, wenn Sie den Einheitskreis betrachten, in dem der Winkel t ist, die „gegenüberliegende“ Seite sin (t) = y ist, die „benachbarte“ Seite cos (t) = x ist und die Hypotenuse 1 ist.
Wir haben zusätzliche Identitäten, die sich auf den Funktionsstatus der Triggerverhältnisse beziehen:
sin(–t) = –sin(t)
cos(–t) = cos(t)
tan(–t) = –tan(t)
Beachten Sie insbesondere, dass Sinus und Tangens ungerade Funktionen sind, die symmetrisch zum Ursprung sind, während Cosinus eine gerade Funktion ist, die symmetrisch zur y-Achse ist. Die Tatsache, dass Sie das „Minus“ -Zeichen des Arguments nach außen (für Sinus und Tangens) oder vollständig (für Cosinus) entfernen können, kann hilfreich sein, wenn Sie mit komplizierten Ausdrücken arbeiten.
Winkel-Summen- und –Differenz–Identitäten
sin(α + β) = sin(α) cos(β) + cos(α) sin(β)
sin(α – β) = sin(α) cos(β) – cos(α) sin(β)
cos(α + β) = cos(α) cos(β) – sin(α) sin(β)
cos(α – β) = cos(α) cos(β) + sin(α) sin(β)
Im obigen Beispiel werden die Winkel übrigens mit griechischen Buchstaben bezeichnet. Der Buchstabe vom Typ a, „α“, wird „Alpha“ genannt, was „AL-fuh“ ausgesprochen wird. Der Buchstabe vom Typ b, „β“, heißt „Beta“, was „BAY-tuh“ ausgesprochen wird.
Inhalt weiter unten
Doppelwinkelidentitäten
sin(2x) = 2 sin(x) cos(x)
cos(2x) = cos2(x) – sin2(x) = 1 – 2 sin2(x) = 2 cos2(x) – 1
Halbwinkelidentitäten
Die obigen Identitäten können durch Quadrieren jeder Seite und verdoppelung aller Winkelmaße. Die Ergebnisse sind wie folgt:
Affiliate

Sum Identities
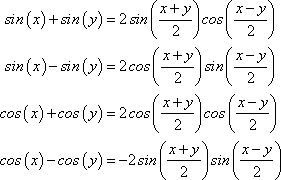
Product Identities
Sie werden alle diese Identitäten oder fast alle verwenden, um andere Triggeridentitäten zu beweisen und Triggergleichungen zu lösen. Wenn Sie jedoch die Infinitesimalrechnung studieren, achten Sie besonders auf die angepassten Sinus- und Cosinus-Halbwinkelidentitäten, da Sie sie häufig in der Integralrechnung verwenden werden.
URL: https://www.purplemath.com/modules/idents.htm