Dieser Abschnitt behandelt:

• Einführung in stückweise Funktionen
• Stückweise Funktionen auswerten
• Stückweise Funktionen grafisch darstellen
• Feststellen, ob eine stückweise Funktion kontinuierlich oder nicht kontinuierlich ist
• Gleichungen aus stückweisen Funktionsgraphen erhalten
• Absolutwert als stückweise Funktion
• Transformationen stückweiser Funktionen
• Stückweise Funktion Textprobleme
• Mehr Übung

Stückweise Funktionen (oder stückweise Funktionen) sind genau das, was sie genannt werden: teile verschiedener Funktionen (Unterfunktionen) in einem Diagramm. Der einfachste Weg, an sie zu denken, ist, wenn Sie mehr als eine Funktion in einem Diagramm gezeichnet haben und nur Teile der Funktionen gelöscht haben, wo sie nicht sein sollen (entlang der \(x\)); Sie sind für verschiedene Intervalle von \ (x\) unterschiedlich definiert. \(y\) ist für verschiedene Werte von \(x\) unterschiedlich definiert; Wir verwenden das \(x\) , um nachzuschlagen, in welchem Intervall es sich befindet, damit wir herausfinden können, was das \ (y\) sein soll.

Beachten Sie, dass es ein Beispiel für die Umkehrung einer stückweisen Funktion hier im Abschnitt Umkehrung der Funktionen gibt.

Here’s an example and graph:

Piecewise Function

Graph

\(\displaystyle f\left( x \right)=\left\{ \begin{align}2x+8\,\,\,\,\,&\text{ if }x\le -2\\{{x}^{2}}\,\,\,\,\,\,\,\text{ }\,&\text{ if }x>-2\end{align} \right.\) (Es gibt andere Möglichkeiten, dies anzuzeigen, z. B. ein „für“ anstelle eines „wenn“ und Kommas oder Semikolons anstelle des „wenn“.) Domäne: \(\mathbb{R},\,\,\,\text{oder}\,\,\left( {-\infty ,\infty } \right)\) Bereich: \(\mathbb{R},\,\,\,\text{oder}\,\,\links( {-\infty ,\infty } \rechts)\)

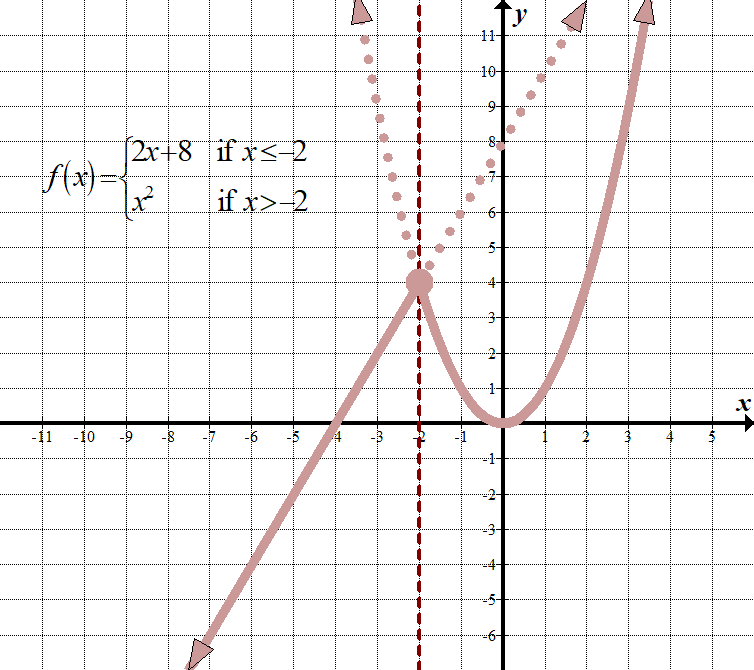Dies bedeutet, dass wir für jedes \ (x\) kleiner oder gleich -2 die Linie \ (2x + 8 \) grafisch darstellen müssen, als wäre es die einzige Funktion im Diagramm. Für jeden \(x\) -Wert größer als -2 müssen wir \({{x}^{2}}\) grafisch darstellen, als wäre es die einzige Funktion im Graphen. Dann müssen wir die Teile „loswerden“, die wir nicht brauchen. Denken Sie daran, dass wir immer noch den Ursprung als Bezugspunkt für beide Diagramme verwenden!

Sehen Sie, wie die vertikale Linie \(x= -2\) als „Grenzlinie“ zwischen den beiden Graphen fungiert?

Beachten Sie, dass der Punkt \((-2,4)\) einen geschlossenen Kreis hat. Technisch gesehen sollte es nur zur Funktion \(2x + 8\) gehören, da diese Funktion das Vorzeichen kleiner als oder Gleich hat, aber da sich der Punkt auch im Diagramm \({{x}^{2}}\) befindet, können wir einfach einen geschlossenen Kreis verwenden, als ob er in beiden Funktionen vorkommt. Siehst du, nicht so schlimm, oder?

Stückweise Funktionen auswerten

Manchmal werden Ihnen stückweise Funktionen gegeben und Sie werden gebeten, sie auszuwerten; mit anderen Worten, finden Sie die \ (y \) -Werte, wenn Sie einen \ (x \) -Wert erhalten. Tun wir dies für \(x= -6\) und \(x=4\) (ohne den Graphen zu verwenden). Hier nochmal die Funktion:

\(\displaystyle f\left( x \right)=\left\{ \begin{align}2x+8\,\,\,\,\,&\text{ wenn }x\le -2\\{{x}^{2}}\,\,\,\,\,\,\,\ text{ }\,&\text{ if }x>-2\Ende{ausrichten} \rechts.\)

Wir wollen zuerst die Bedingungen rechts betrachten, um zu sehen, wo unser \(x\) ist. Wenn \(x=-6\) , wissen wir, dass es kleiner als -2 ist, also schließen wir unser \(x\) nur an \ (2x+ 8\) an. \(f(x)\) oder \(y\) ist \((2)(-6)+8=-4\). Wir kümmern uns nicht einmal um das \(\boldsymbol{{x}^{2}}\)! So einfach geht’s. Sie können auch sehen, dass wir dies richtig gemacht haben, indem Sie die obige Grafik verwenden.

Versuchen Sie nun \(x=4\). Wir schauen zuerst nach rechts und sehen, dass unser \(x\) größer als -2 ist, also stecken wir es in das \({{x}^{2}}\). (Wir können diesmal einfach das \ (2x+8\) ignorieren.) \(f(x)\) oder \(y\) ist \({{4}^{2}}=16\).

Stückweise Funktionen grafisch darstellen

Sie werden wahrscheinlich aufgefordert, stückweise Funktionen grafisch darzustellen. Manchmal enthalten die Diagramme Funktionen, die nicht kontinuierlich oder diskontinuierlich sind, was bedeutet, dass Sie Ihren Stift in der Mitte des Diagramms aufnehmen müssen, wenn Sie es zeichnen (wie ein Sprung!). Kontinuierliche funktionen bedeutet, dass sie nie zu holen ihre bleistift wenn sie waren zu ziehen sie von links nach rechts.

Und denken Sie daran, dass die Graphen nur dann wahre Funktionen sind, wenn sie den vertikalen Linientest bestehen.

Zeichnen wir diese stückweisen Funktionen und bestimmen, ob sie kontinuierlich oder nicht kontinuierlich sind. Beachten Sie, wie wir jede Funktion so zeichnen, als wäre sie die einzige, und dann die nicht benötigten Teile „löschen“. Wir erhalten auch die Domäne und den Bereich, wie wir es hier im Abschnitt Algebraische Funktionen getan haben.

Piecewise Function	Graph
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-2x+8\,\,\,\,\,\,\text{if }x\le 4\\\frac{1}{2}x-2\,\,\,\,\,\,\,\,\,\text{if }x>4\end{array} \right.\) Continuous Domain: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) Range: \(\left( {0,\infty } \right)\)
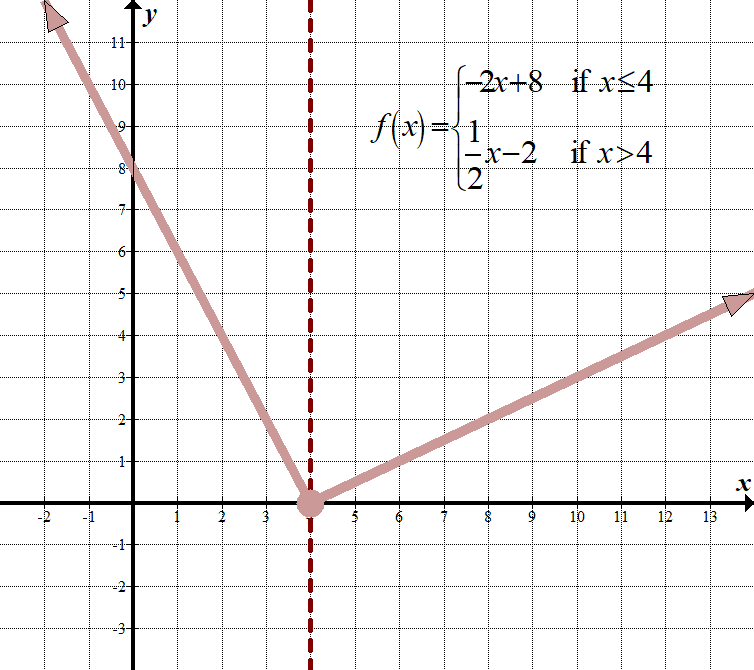\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\,\text{if }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1}\le x<4\\x-5\,\,\,\,\,\,\,\,\,\text{if }x\ge 4\end{array} \right.\) Non-Continuous Domain: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) Range: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\)

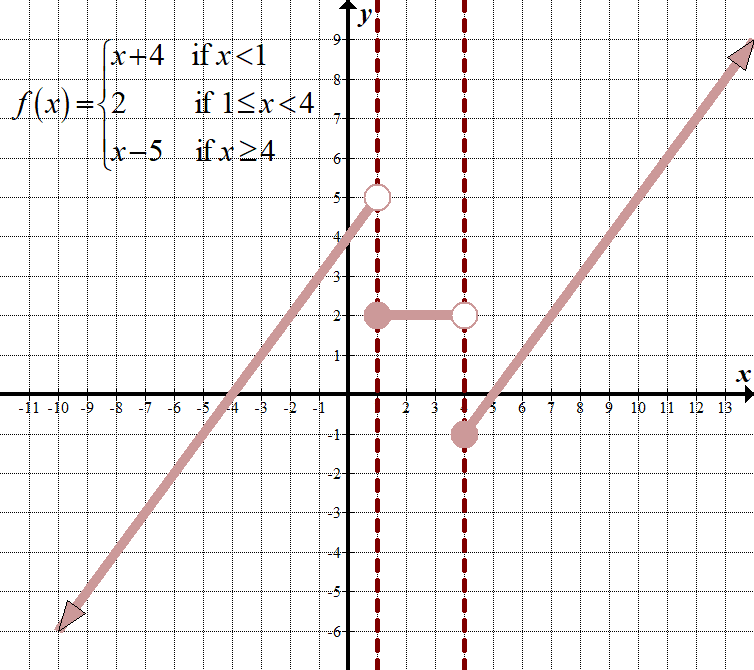We can actually put piecewise functions in the graphing calculator:

Piecewise Function Screens

Steps and Notes

Enter the piecewise function on three lines: Hier ist der Graph:

Um die stückweise Funktion \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\,\ text{wenn }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ text{wenn 1 }\le x<4\\-5+x\,\,\,\,\,\ text {if } x\ ge 4\ Ende {array} \rechts.\) im Taschenrechner können Sie die Funktion in drei Zeilen eingeben, indem Sie die Funktion in jedem Intervall durch eine „Testungleichheit“ dieses Intervalls dividieren (und Klammern beachten!). Der Grund, warum wir durch die Intervalle oder Ungleichungen dividieren, ist, dass der Rechner eine 1 zurückgibt, wenn die Ungleichung (wie \(x<1\)) wahr ist; Zum Beispiel endet \((x+4)\) nur \((x+4)/(1)\), wenn \(x<1\). Wenn \(x\ge 1\) , dividieren wir durch 0, so dass nichts gezeichnet wird. Hier ist, was wir in den Rechner setzen können: \(\displaystyle \begin{array}{l}{{Y}_{1}}=\links( {x+4} \rechts)/\links( {x<1} \rechts)\\{{Y}_{2}}=\links( 2 \rechts)/\links( {x\ge 1\text{ und }x<4} \right)\\{{Y}_{3}}=\left( {-5+x} \right)/\left( {x\ge 4} \right)\end{array}\) (Beachten Sie, dass Sie dies auch in einer Zeile eingeben können, indem Sie die Bedingungen multiplizieren, anstatt sie zu dividieren, und Pluszeichen zwischen jeder der drei Funktionen / Intervalle: \(\displaystyle {{Y}_{1}}=\links( {x+4} \rechts)\links( {x<1} \rechts)+\links( 2 \rechts)\links( {x\ge 1\text{ und }x<4} \rechts)+\links( {-5+x} \rechts)\links( {x\ge 4} \rechts)\).) Hier sind die Tastenanschläge für die Verwendung von drei Zeilen. Beachten Sie, dass Sie die 2. MATHEMATIK (TEST) verwenden, um zu dem Bildschirm zu gelangen, der \ (\ le \), \ (\ ge \) usw. enthält. Zum Beispiel erhält 2. MATHEMATIK 6 Sie \ (\le \). Verwenden Sie 2. MATHEMATIK (TEST), rechts zur LOGIK, dann 1, für das „und“ in \({{Y}_{2}}\).

So erkennen Sie, ob eine stückweise Funktion kontinuierlich oder nicht kontinuierlich ist

Um festzustellen, ob ein stückweiser Graph kontinuierlich oder nicht kontinuierlich ist, können Sie sich die punkte und sehen, ob der \ (y \) Punkt an jedem von ihnen gleich ist. (Wenn die \(y\) ’s anders wären, gäbe es einen „Sprung“ in der Grafik!)

Versuchen wir dies für die Funktionen, die wir oben verwendet haben:

Piecewise Function	Check Boundary Points
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-2x+8\,\,\,\,\,\,\,\text{if }x\le 4\\\frac{1}{2}x-2\,\,\,\,\,\,\,\,\,\,\text{if }x>4\end{array} \right.\)	Let’s check \(x=4\) in both parts of the function, since 4 is the „boundary point”: \(\begin{array}{l}-2(4)+8=0\\\,\,\,\ frac{1}{2}(4)-2=0\end{array}\) Da \(0=0\), ist diese stückweise Funktion kontinuierlich.
\(\displaystyle f\links( x \rechts)=\links\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\,\,\,\,\,\ text{wenn }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ text{wenn 1 }\le x<4\\-5+x\,\,\,\,\,\,\,\,\,\ text {if } x\ ge 4\ Ende {array} \rechts.\)	Überprüfen wir die ersten beiden Teile der Funktion. Beachten Sie im zweiten Teil, \(y\) ist immer 2: \(\begin{array}{l}1+4=5\\\,\,\,\,\,\,\,\,\,2=2\ end{array}\) Seit \(5\ne 2\) können wir hier anhalten und beachten, dass diese stückweise Funktion nicht kontinuierlich ist. Wenn die \(y\) ’s gleich wären, müssten wir eins gehen, um den nächsten Grenzpunkt bei \(x= 4\) zu überprüfen.

Erhalten von Gleichungen aus stückweisen Funktionsgraphen

Möglicherweise werden Sie aufgefordert, eine stückweise Funktion in einem Diagramm zu schreiben. Jetzt, da wir wissen, worum es bei stückweisen Funktionen geht, ist es nicht so schlimm!

Um zu überprüfen, wie man Gleichungen aus linearen Graphen erhält, siehe Erhalten der Gleichungen einer Linie und von Quadratics, siehe Finden einer quadratischen Gleichung aus Punkten oder einem Graphen.

Hier sind die Graphen mit Erklärungen, wie man ihre stückweisen Gleichungen ableitet:

Piecewise Function Graph	Procedure to get Function
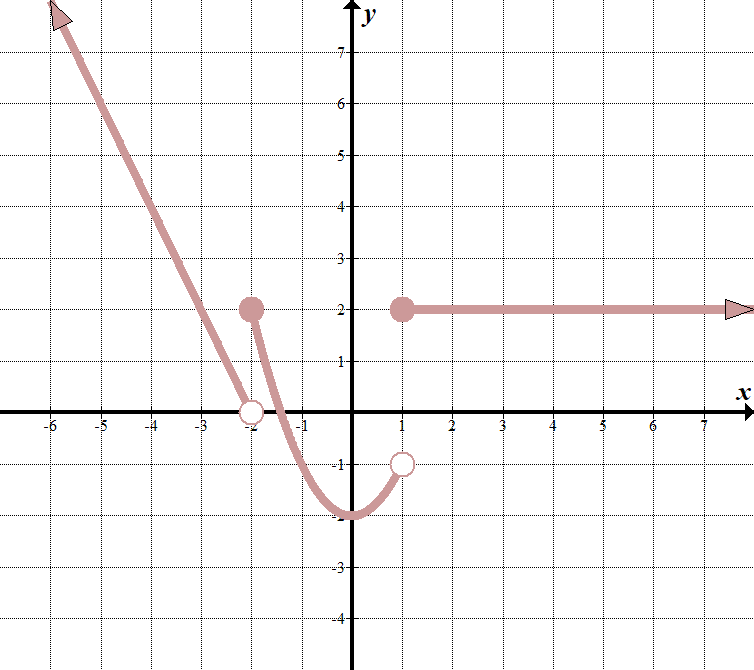	We see that our „boundary lines” are at \(x=-2\) and \(x=1\). We know that our function will look something like this (notice open and closed endpoints): \(\displaystyle f\links( x \rechts)=\links\{ \begin{array}{l}\text{ }……\,\,\,\,\,\,\,\,\ text{wenn }x<-2\\\text{ }……\,\,\,\,\,\,\,\,\ text{if }-\text{2 }\le x<1\\\text{ }……\,\,\,\,\,\,\,\,\ text {if } x\ge 1\ Ende {array} \rechts.\) Wir können zwei Punkte \((-2,0)\) und \((-3,2)\) ganz links auswählen, um die Gleichung \(y=-2x-4\) zu erhalten. Die mittlere Funktion ist \(y={{x}^{2}}-2\), und die Funktion ganz rechts ist nur die horizontale Linie \(y = 2\). Somit ist die stückweise Funktion: \(\displaystyle f\links( x \rechts)=\links\{ \begin{array}{l}-2x-4\,\,\,\,\,\,\,\ text{wenn }x<-2\\\text{ }{{x}^{2}}-2\,\,\,\,\,\,\,\,\,\,\ text{if }-\text{2}\le x<1\\\text{ 2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ text {if } x\ge 1\ Ende {array} \rechts.\)
	Wir sehen, dass unsere „Grenzlinie“ bei \(x=5\) liegt. Da sich die Zeilen bei \((5,4)\) treffen, spielt es keine Rolle, wo wir das Zeichen \(\le \) oder \ (\ge \) setzen; wir können es einfach nicht an beiden Stellen platzieren, sonst wäre es keine Funktion. Wir haben bisher: \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }……\,\,\,\,\,\,\,\,\,\ text{wenn }x<5\\\text{ }……\,\,\,\,\,\,\,\,\,\ text {if } x\ ge 5\ Ende {array} \rechts.\) Auch hier müssen wir jede Zeile einzeln betrachten, um ihre Gleichungen zu bestimmen. Wir können entweder 2 Punkte von jeder Linie nehmen, um diese zu erhalten, oder aus Steigungen und \ (y \) –Abschnitten ableiten; Die stückweise Funktion ist: \(\displaystyle f\links( x \rechts)=\links\{ \begin{array}{l}\frac{6}{5}x-2\,\,\,\,\,\,\,\ text{wenn }x<5\\\frac{2}{5}x+2\,\,\,\,\,\,\,\ text {if } x\ ge 5\ Ende {array} \rechts.\)

Absolutwert als stückweise Funktion

Wir können Absolutwertfunktionen als stückweise Funktionen schreiben – es ist wirklich cool! Möglicherweise möchten Sie das Lösen von Absolutwertgleichungen und Ungleichungen überprüfen, bevor Sie mit diesem Thema fortfahren.Nehmen wir an, wir haben die Funktion \(f\left( x \right)=\left| x \right|\) . Von dem, was wir früher gelernt haben, wissen wir, dass, wenn \(x\) positiv ist, da wir den absoluten Wert nehmen, es immer noch nur \(x\) sein wird. Aber wenn \(x\) negativ ist, wenn wir den absoluten Wert nehmen, müssen wir das Gegenteil nehmen (negieren), da der absolute Wert positiv sein muss. Sinnvoll? Wenn wir zum Beispiel \(|5|\) hätten, nehmen wir einfach das, was sich innerhalb des absoluten Vorzeichens befindet, da es positiv ist. Aber für \(|-5/\) müssen wir das Gegenteil (negativ) von dem nehmen, was sich innerhalb des absoluten Wertes befindet, um es zu \(\displaystyle 5\,\,\,(-\,-5=5)\).

Dies bedeutet, dass wir diese Absolutwertfunktion als stückweise Funktion schreiben können. Beachten Sie, dass wir den „Wendepunkt“ oder „Grenzpunkt“ erhalten können, indem wir alles, was sich innerhalb des Absolutwerts befindet, auf 0 setzen. Dann verwenden wir entweder die ursprüngliche Funktion oder negieren die Funktion, abhängig vom Vorzeichen der Funktion (ohne den absoluten Wert) in diesem Intervall.Zum Beispiel können wir schreiben \(\displaystyle \left/ x \right/\text{ }=\left\{ \begin{array}{l}x\,\,\,\,\,\,\,\,\,\ text {wenn } x\ge 0\\-x\,\,\,\,\,\ text{if }x<0\Ende{array} \rechts.\). Beachten Sie auch, dass, wenn die Funktion kontinuierlich ist (es gibt keinen „Sprung“) am Grenzpunkt, es keine Rolle spielt, wo wir die Zeichen „kleiner als oder gleich“ (oder „größer als oder gleich“) setzen, solange wir sie nicht wiederholen! Wir können sie nicht wiederholen, weil wir theoretisch nicht zwei Werte von \(y\) für dasselbe \ (x\) haben können, sonst hätten wir keine Funktion.

Here are more examples, with explanations. (You might want to review Quadratic Inequalities for the second example below):

Absolute Value Function	Method to get Piecewise Function
\(g\left( x \right)=\left| {2x+3} \right|\)	Let’s first find the „boundary line”. Wir tun dies, indem wir den absoluten Wert auf 0 setzen und dann nach \(\boldsymbol{x}\) . Wenn \(2x+3\ge 0\), erhalten wir \(\displaystyle x\ge -\frac{3}{2}\) (eigentlich können wir das \(\ge \) behalten, wenn wir lösen). Wenn \(2x+3\) positiv ist, nehmen wir es einfach „wie es ist“, aber wenn es negativ ist, müssen wir das Ganze negieren. Daher ist die stückweise Funktion: \(\displaystyle \links/ {2x+3} \rechts/=\links\{ \begin{array}{l}2x+3\,\,\,\,\,\,\,\,\,\ text {wenn } x \ge -\frac {3} {2}\text{ }\\-2x-3\,\,\,\,\,\ text{if }x<-\frac{3}{2}\end{array} \rechts.\) Probieren Sie es aus – es funktioniert!
\(f\left( x \right)=\left| {{{x}^{2}}-4} \right/\)	Suchen wir zuerst die „Grenzlinie (n)“; Wir setzen den absoluten Wert auf 0. Wenn \({{x}^{2}}-4\ge 0\), erhalten wir \(x\le -2\) oder \(x\ge 2\) (versuchen Sie einige Zahlen!). Wenn \({{x}^{2}} -4\) positiv ist, nehmen wir es einfach „wie es ist“, aber wenn es negativ ist, müssen wir es negieren. Die stückweise Funktion ist: \(\displaystyle \left/ {{{x}^{2}}-4} \right/=\left\{ \begin{array}{l}{{x}^{2}}-4\,\,\,\,\,\ text {wenn } x\le -2\\4-{{x}^{2}}\,\,\,\,\,\ text{if }-2<x<2\\{{x}^{2}}-4\,\,\,\,\,\ text {if } x \ ge 2\ text{ } \ Ende {array} \rechts.\) oder \(\displaystyle \left/ {{{x}^{2}}-4} \right/=\left\{ \begin{array}{l}{{x}^{2}}-4\,\,\,\,\,\,\ text{wenn }x\le -2\text{ }\,\,\text{oder}\,\,\text{ }x\ge 2\\4-{{x}^{2}}\,\,\,\,\,\,\,\ text{if }-2<x<2\Ende{array} \rechts.\) Da die Funktion kontinuierlich ist, spielt es keine Rolle, wo wir \(\le \) und \(\ge \) haben (im Gegensatz zu \(<\) und \(>\)), solange wir sie nicht wiederholen.
\(f\left( x \right)=2x+\left| {x+2} \right/\)	Dieser ist etwas kniffliger, da wir ein \(x\) innerhalb und außerhalb des absoluten Wertes haben. Für die „Grenzlinie“ verwenden wir nur das, was sich innerhalb des Absolutwerts befindet. Wenn \(x+2\ge 0\) , erhalten wir \(x\ge -2\). Aber für die stückweise Funktion müssen wir die gesamte Funktion verwenden, einschließlich des Teils, der außerhalb des absoluten Wertes liegt. Die stückweise Funktion ist also: \(\displaystyle 2x+\links/ {x+2} \rechts/=\links\{ \begin{array}{l}2x+x+2\,\,\,\,\,\ text {wenn } x\ge -2\\2x-x-2\,\,\,\,\,\ text{if }x<-2\Ende{array} \rechts.\) Vereinfachen wir: \(\displaystyle 2x+\left/ {x+2} \right|=\left\{ \begin{array}{l}3x+2\,\,\,\,\,\,\,\ text {wenn } x \ge -2\\x-2\,\,\,\,\,\,\,\,\,\,\ text{if }x<-2\Ende{array} \rechts.\) Versuchen Sie einige Werte kleiner als und größer als -2; sie sollten funktionieren!
\(g\left( x \right)=\left| {{{x}^{2}}-4x-5} \right/\)	Dieses Problem lässt sich am besten mit einem Vorzeichendiagramm lösen, da wir eine quadratische haben und wissen müssen, wo die Funktion positiv und negativ ist. Faktorisieren Sie zuerst das Quadrat innerhalb der Absolutwertfunktion zu \(\left( {x-5} \right)\left( {x+1} \right)\) . Verwenden Sie dann ein Vorzeichendiagramm, um zu sehen, wo die Faktoren positiv und negativ sind, und denken Sie daran, dass wir bei positiven Faktoren die Funktion „wie besehen“ verwenden und bei negativen Faktoren die Funktion negieren: \(\displaystyle \links/ {{{x}^{2}}-4x-5} \rechts|=\links\{ \begin{array}{l}{{x}^{2}}-4x-5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ text {wenn } x\le -1\,\,\,\,\ text{oder}\,\,\,\,x\ge 5\\-\links( {{{x}^{2}}-4x-5} \rechts)\,\,\,\,\ text{if }-1<x<5\text{ }\Ende{array} \rechts.\)
\(\displaystyle g\left( x \right)=\frac{{\left| {x+2} \right|}}{{x+2}}\)	eine rationale Funktion, da es eine Variable im Nenner gibt. Wenn \(x+2\ge 0\), erhalten wir \(\displaystyle x\ge -2\). Wenn \(x+2\) positiv ist, nehmen wir es einfach „wie es ist“, aber wenn es negativ ist, müssen wir negieren, was im absoluten Wert ist: \(\displaystyle \frac{{\left| {x+2} \right|}}{{x+2}}=\left\{ \begin{array}{l}\frac{{x+2}}{{x+2}}\,\,\,\,\,\,\,\,\,\ text {wenn } x\ge -2\\\frac{{-x-2}}{{x+2}}\,\,\,\,\,\,\ text{if }x<-2\Ende{array} \rechts.\). Aber wir müssen vorsichtig sein, da \(x\ne 2\) (Domänenbeschränkung: Der Nenner wäre 0). Daher ist die stückweise Funktion: \(\displaystyle \frac{{\links| {x+2} \rechts|}}{{x+2}}=\links\{ \begin{array}{l}1\,\,\,\,\,\,\,\,\,\,\ text{wenn }x>-2\\-1\,\,\,\,\,\,\ text{if }x<-2\Ende{array} \rechts.\).

Möglicherweise werden Sie auch aufgefordert, ein Absolutwertdiagramm als stückweise Funktion zu schreiben:

Absolute Value Graph	Method to get Piecewise Function
	We see that our „boundary line” is at \(x=0\), so what’s inside the absolute value sign must be \(x\) or a factor of \(x\). (Dies liegt daran, dass wir die Grenzlinie mit einer Absolutwertfunktion auf 0 setzen und nach \(x\) lösen, um die Grenzlinie mit einer Absolutwertfunktion zu erhalten). Wenn \(x>0\), können wir sehen, dass die Gleichung der Linie \(y=2x-2\) . Wenn \(x<0\), lautet die Gleichung \(y=2x-2\). Wir können dies als stückweise Funktion schreiben: \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}2x-2\,\,\,\,\,\,\,\ text{if }x>0\\-2x-2\,\,\,\text{if }x\le 0\Ende{array} \rechts.\) Wir können dies auch als transformierte Absolutwertfunktion schreiben: \(y=2\left| x \right|-2\) oder \(y=\left| {2x} \right|-2\) (da 2 positiv ist, kann es innerhalb oder außerhalb von \(\left| {\,\,} \right/\) ). (Dies ist sinnvoll, da, wenn das, was in der \(\left| {\,\,} \right|\) ist \(> 0\), wir verwenden die reguläre Funktion \(y=2x-2\), und wenn das, was in der ist \(< 0\), negieren wir den Absolutwertteil, um ihn \(y=-\left( {2x} \right) -2\)).
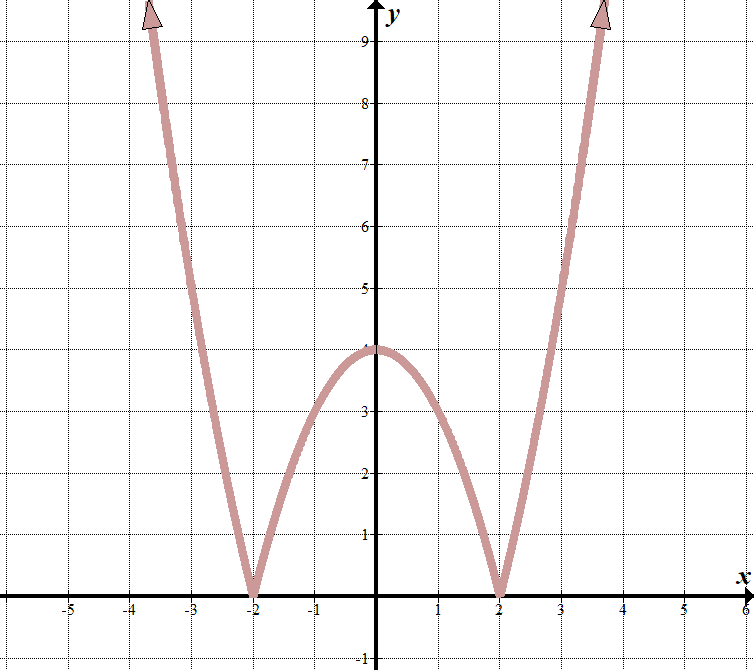	Wir sehen, dass unsere „Grenzlinien“ bei \(x= 2\) und \(x=-2\) liegen, also muss das, was sich im Absolutwertzeichen befindet, Faktoren von \(x-2\) und \(x+2\). Wenn \(x<-2\) oder \(x>2\), können wir sehen, dass das Diagramm wie der normale Teil des Diagramms aussieht \(y={{x}^{2}}-4\). (Ich habe das herausgefunden, indem ich die Faktoren kannte und eine gute Vermutung machte!) Wenn \(-2<x<2\) , wird die Gleichung umgedreht oder negiert (um die \(x\) -Achse gedreht). Wir können dies als stückweise Funktion schreiben: \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}{{x}^{2}}-4\,\,\,\,\,\,\,\,\,\ text{wenn }x<-2\text{ oder }x>2\\-{{x}^{2}}\text{+ 4}\,\,\,\,\,\,\ text{if }-2\le x\le 2\Ende {array} \rechts.\) Wir können sehen, dass dies eine transformierte quadratische Funktion \(y={{x}^{2}}-4\) mit einem absoluten Wert um sie herum begann, da alle \(y\) Werte positiv sind: \(y=\left| {{{x}^{2}}-4} \right/\).
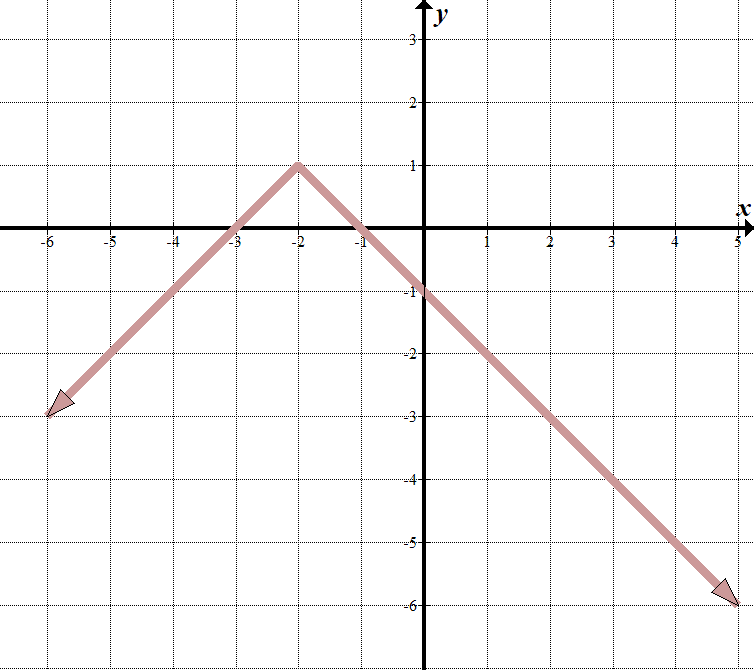	Wir sehen, dass unsere „Grenzlinie“ bei \(x= -2\) liegt, also muss das absolute Wertzeichen \(x+2\) sein. Wenn \(x>-2\), können wir sehen, dass die Gleichung der Linie \(y=-x-1\) . Wenn \(x<-2\) , ist die Zeile \(y=x+3\). Wir können dies als stückweise Funktion schreiben: \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-x-1\,\,\,\,\,\,\ text{wenn }x>-2\\x+3\,\,\,\,\,\,\,\,\,\,\ text{if }x\le -2\end{array} \rechts.\) Es ist wahrscheinlich einfacher, dies als transformierte Absolutwertfunktion zu schreiben. Wir können sehen, dass die übergeordnete Absolutwertfunktion vertikal gespiegelt wird, nach links 2 und nach oben 1. Unsere Absolutwertgleichung ist \(y=-\left/ {x+2} \right|\,\,+\,\,1\). Dies ist die gleiche wie die stückweise Funktion oben. Probieren Sie es aus – es funktioniert!

Transformationen von stückweisen Funktionen

Machen wir eine Transformation einer stückweisen Funktion. Wir haben hier im Abschnitt Übergeordnete Diagramme und Transformationen mehr über übergeordnete Funktionen und deren Transformationen erfahren. Sie werden wahrscheinlich zuerst diesen Abschnitt lesen wollen, bevor Sie eine stückweise Transformation versuchen.

Lassen Sie uns die folgende stückweise Funktion um die \(x\) -Achse drehen, vertikal um den Faktor 2 Einheiten, 1 Einheit nach rechts und 3 Einheiten nach oben gedehnt.

Wir zeichnen \(-2f\left( x-1 \right)+3\), wobei:

\(\displaystyle f\left( x \right)=\left\{ \begin{align}x+4\,\,\,\,\,\,\,\,&\text{ wenn }x<&\text{ wenn 1 }\le x<4\\x-5\,\,\,\,\,\,\,\,&\text{ wenn }x\ge 4\Ende{ausrichten} \rechts.\)

Stellen wir sicher, dass wir die „Begrenzungspunkte“ verwenden, wenn wir das t-Diagramm für die Transformation ausfüllen. Denken Sie daran, dass die Transformationen innerhalb der Klammern an \ (x\) (die entgegengesetzte Mathematik) und außerhalb an \ (y\) erfolgen. Um ein T-Diagramm zu erstellen, wie in der folgenden Tabelle gezeigt, können wir Schlüsselpunkte verwenden, einschließlich zwei Punkte auf jeder der „Grenzlinien“.

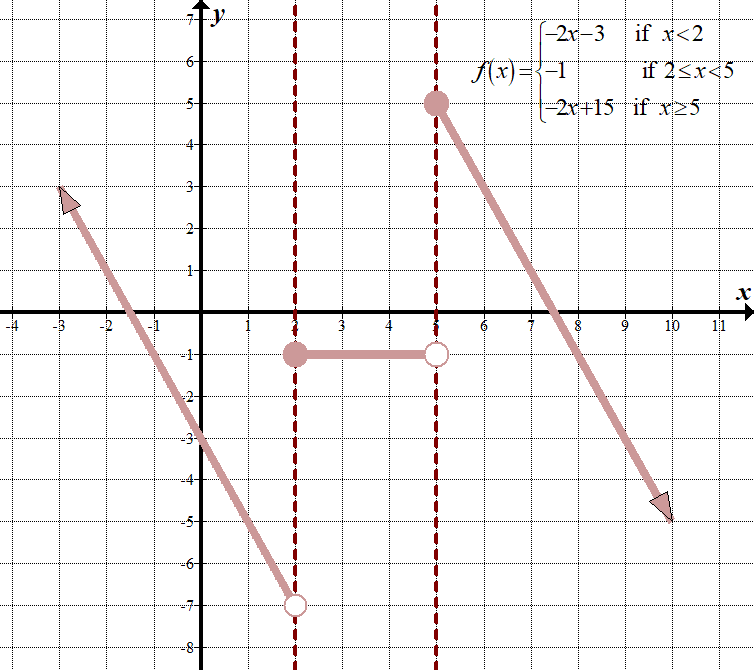
Beachten Sie, dass wir, da diese Transformation kompliziert ist, eine neue stückweise Funktion erstellen können, indem wir die 3 „Teile“ transformieren und auch die „\ (x\)“ transformieren, an denen sich die Grenzpunkte befinden (Addieren 1, oder nach rechts gehen 1), da wir die entgegengesetzte Mathematik für die „\ (x\)“ ausführen. Um die neuen Funktionen in jedem Intervall zu erhalten, können wir einfach „\ (x-1 \)“ durch „\ (x\)“ in der ursprünglichen Gleichung ersetzen, mit -2 multiplizieren und dann 3 addieren. Zum Beispiel \(\displaystyle -2f\left( {x-1} \right)+3=-2\left+3=-2\left( {x+3} \right)+3=-2x-3\).

\(\displaystyle -2f\links( {x-1} \rechts)+3=\links\{ \begin{array}{l}-2\links( {\links( {x-1} \rechts)+4} \rechts)+3=-2x-3,\,\,\,\,\ text{ if }x-1<1\,\,\,\links( {x<2} \rechts)\\-2\links( 2 \rechts)+3=-1,\,\,\,\,\ text{ if }\,\text{ 2 }\le x<5\\-2\links( {\ links( {x-1} \rechts)-5} \rechts)+3=-2x+15,\,\,\,\,\ text { if } x\ ge 5\ Ende {array} \rechts.\)

Hier sind die Diagramme „Vorher“ und „Nachher“, einschließlich des T-Diagramms:

Piecewise Parent Function	T-chart	Transformation of Function
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\text{if }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1 }\le x<4\\x-5\,\,\,\,\,\,\,\,\text{if }x\ge 4\end{array} \right.\)	x + 1 x y –2y+3 1 0 4 –5 2 1 5 –7 2 1 2 –1 5 4 2 –1 5 4 –1 5 8 7 2 –1	\(\displaystyle -2f\left( {x-1} \right)+3=\left\{ \begin{array}{l}-2x-3\,\,\,\,\,\,\,\,\,\text{if }x<2\\-1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 2}\le x<5\\-2x+15\,\,\,\,\,\,\text{if }x\ge 5\end{array} \right.\)

Piecewise Function Word Problems

Problem:

Ihr Lieblingshundepfleger wird entsprechend dem Gewicht Ihres Hundes berechnet. Wenn Ihr Hund 15 Pfund und darunter ist, berechnet der Groomer $ 35. Wenn Ihr Hund zwischen 15 und 40 Pfund wiegt, berechnet er 40 US-Dollar. Wenn Ihr Hund über 40 Pfund wiegt, berechnet er 40 US-Dollar plus 2 US-Dollar für jedes Pfund.

(a) Schreiben Sie eine stückweise Funktion, die beschreibt, was Ihr Hundepfleger berechnet.

(b) Zeichne die Funktion.

(c) Was würde der Groomer berechnen, wenn Ihr süßer Hund 60 Pfund wiegt?

Lösung:(a) Wir sehen, dass die „Grenzpunkte“ 15 und 40 sind, da dies die Gewichte sind, an denen sich die Preise ändern. Da wir zwei Grenzpunkte haben, haben wir drei Gleichungen in unserer stückweisen Funktion. Wir müssen bei 0 beginnen, da Hunde über 0 Pfund wiegen müssen:

\(\displaystyle f\links( x \rechts)=\links\{ \begin{array}{l}\text{ }……\,\,\,\,\,\,\,\,\,\ text{wenn }0<x\le 15\\\text{ }……\,\,\,\,\,\,\,\,\,\ text{wenn }15<x\le 40\\\text{ }……\,\,\,\,\,\,\,\,\,\ text{if }x>40\Ende{array} \rechts.\)

Wir suchen die „Antworten“ (wie viel die Pflege kostet) auf die „Fragen“ (wie viel der Hund wiegt) für die drei Preisklassen. Die ersten beiden sind nur Pauschalgebühren (35 USD bzw. 40 USD). Die letzte Gleichung ist etwas schwieriger; der Groomer berechnet $ 40 plus $ 2 für jedes Pfund über 40. Versuchen wir es mit reellen Zahlen: Wenn Ihr Hund 60 Pfund wiegt, berechnet er $ 40 plus $ 2 mal \ (20 (60-40) \). Wir machen daraus eine Gleichung: \(40+ 2 (x–40) \), die sich zu \ (2x–40 \) vereinfacht (siehe wie 2 ist die Steigung?).

Die ganze stückweise Funktion ist:

\(\displaystyle f\links( x \rechts)=\links\{ \begin{array}{l}\text{ }35\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ text{wenn }0<x\le 15\\\text{ }40\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ text{if }15<x\le 40\\\text{ }40+2\links( {x-40} \rechts)\,\,\,\,\,\,\ text{if }x>40\Ende{array} \rechts.\) oder \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }35\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ text{wenn }0<x\le 15\\\text{ }40\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ text{wenn }15<x\le 40\\\text{ }2x-40\,\,\,\,\,\,\,\ text{if }x>40\Ende{array} \rechts.\)

(b) Let’s graph:Beachten Sie, dass diese stückweise Gleichung nicht kontinuierlich ist. Beachten Sie auch, dass eine vernünftige Domain für dieses Problem \(\left( {0,200} \right]\) sein könnte (vorausgesetzt, Hunde wiegen nicht mehr als 200 Pfund!) und ein vernünftiger Bereich könnte \(\left\cup \left\) .

(c) Wenn Ihr Hund 60 Pfund wiegt, können wir entweder die Grafik oder die Funktion verwenden, um zu sehen, dass Sie $ 80 bezahlen müssten. Whoa! Das kostet mehr als ein menschlicher Haarschnitt (zumindest meine Haarschnitte)!

Problem:

Sie planen, She Love Math T-Shirts als Spendenaktion zu verkaufen. Die großhandel t-shirt unternehmen gebühren sie $10 ein hemd für die erste 75 shirts. Nach den ersten 75 Hemden, die Sie bis zu 150 Hemden kaufen, senkt das Unternehmen den Preis auf 7,50 USD pro Hemd. Nachdem Sie 150 Hemden gekauft haben, sinkt der Preis auf 5 USD pro Hemd. Schreiben Sie eine Funktion, die diese Situation modelliert.

Lösung:

Wir sehen, dass die „Grenzpunkte“ 75 und 150 sind, da dies die Anzahl der gekauften T-Shirts ist, bei denen sich die Preise ändern. Da wir zwei Grenzpunkte haben, haben wir drei Gleichungen in unserer stückweisen Funktion. Wir beginnen mit \(x\ge 1\), da wir davon ausgehen, dass mindestens ein Hemd gekauft wurde. Hinweis In diesem Problem muss die Anzahl der gekauften T-Shirts (\(x\)) oder die Domain eine Ganzzahl sein, aber diese Einschränkung sollte das Ergebnis des Problems nicht beeinflussen.

\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }……\text{ wenn }1\le x\le 75\\\text{ }……\text{ wenn }75<x\le 150\\\text{ }.. ….\text{ if }x>150\Ende{array} \rechts.\)

Wir suchen die „Antworten“ (Gesamtkosten der T-Shirts) auf die „Fragen“ (wie viele gekauft werden) für die drei Preisklassen.

Für bis zu 75 Hemden beträgt der Preis $ 10, also wäre der Gesamtpreis \(10x\). Für mehr als 75 Hemden, aber bis zu 100 Hemden, betragen die Kosten 7,50 USD, aber die ersten 75 T-Shirts kosten immer noch 10 USD pro Hemd. Die zweite Funktion umfasst die 750 US-Dollar, die für die ersten 75 Hemden ausgegeben wurden (75 mal 10 US-Dollar), sowie das 7,50-fache der Anzahl der Hemden über 75, was \ ((x-75) \) wäre. Wenn Sie beispielsweise 80 Hemden gekauft haben, müssen Sie \ (\ $ 10 \ mal 75 = \ $ 750 \) plus \ (\ $ 7.50 \ mal) ausgeben 5\,\) (80 – 75) für die Hemden nach dem 75.

In ähnlicher Weise würden wir für über 150 Hemden immer noch den $ 10-Preis bis zu 75 Hemden, den $ 7, bezahlen.50 Preis für 76 bis 150 Hemden (75 weitere Hemden) und dann 5 USD pro Hemd für die Anzahl der über 150 gekauften Hemden. Wir zahlen \(10(75)+7.50(75)+5( x-150)\) für \(x\) Hemden. Geben Sie Zahlen ein und probieren Sie es aus!

Die ganze stückweise Funktion ist:

\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }10x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ text {wenn } 1\le x\le 75 \\\ text { } 7.5x\text{ } +\text{ }187.5\,\,\,\,\,\ text{wenn 7}5<x\le 150\\\text{ }5x+562.5\,\,\,\,\,\,\,\,\,\,\ text{ if }x>150\Ende{array} \rechts.\) oder \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}\text{ }10x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ text {wenn } 1\le x\le 75 \\\ text { } 7.5x\text{ } +\text{ }187.5\,\,\,\,\,\ text{wenn 7}5<x\le 150\\\text{ }5x+562.5\,\,\,\,\,\,\,\,\,\,\,\ text{if }x>150\Ende{array} \rechts.\)

Problem:

Ein Busservice kostet $ 50 für die ersten 400 Meilen, und jede weitere 300 Meilen (oder ein Bruchteil davon) fügt $ 10 zum Fahrpreis hinzu.

Verwenden Sie eine stückweise Funktion, um den Bustarif in Bezug auf die Entfernung in Meilen darzustellen.

Lösung:

Dies ist eigentlich ein kniffliges Problem, aber denken wir zuerst an den „Grenzpunkt“, der 400 ist. Es ist ziemlich einfach, wenn die Fahrt weniger als 400 Meilen ist; Die Kosten betragen $ 50.

Für mehr als 400 Meilen müssen wir die ersten 400 Meilen abziehen (aber denken Sie daran, die ersten $ 50 einzubeziehen), die Anzahl der verbleibenden Meilen durch 300 Meilen teilen (und aufrunden, wenn es einen Bruchteil gibt) Betrag) und multiplizieren Sie das mit $ 10.

Der knifflige Teil ist, wenn wir einen Teil der nächsten 300 Meilen „zusammenrunden“. Wir können eine „ceiling“ -Funktion verwenden (bezeichnet mit \(\left\lceil {} \right\rceil \)); Diese Funktion gibt die kleinste ganze Zahl an, die größer oder gleich ihrer Eingabe ist; Zum Beispiel ist die Obergrenze von 3,5 und 4 4.

Das ist es also, was wir haben:

\(\displaystyle f\left( x \right)=\links\{ \begin{array}{l}\text{ }50\text{ }\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\ text{if }0\le x\le 400\\\text{ }50+10\mal \links\lceil {\frac{{x-400}}{{300}}} \ rechts \ rceil \text{ }\,\,\,\,\,\,\ text{ if }x>400\Ende{array} \rechts.\)

Probieren wir es aus! Wenn wir eine 1500-Meilen-Fahrt haben, wären die Kosten \(\displaystyle 50+10\times \left\lc) {\frac{{1500-400}}{{300}}} \ rechts\rceil \text{ }=50+10\mal 4 =\$90\).

Problem:

Welcher Wert von \(\boldsymbol{a}\) würde diese stückweise Funktion stetig machen?

\(\displaystyle f\links( x \rechts)=\links\{ \begin{array}{l}3{{x}^{2}}+4\,\,\,\,\,\ text{ wenn }x<-2\\5x+\boldsymbol{a}\,\,\,\,\,\,\,\,\ text {if } x\ ge -2\ Ende {array} \rechts.\)

Lösung:

Damit die stückweise Funktion kontinuierlich ist, müssen am Grenzpunkt (wo sich die Funktion ändert) die beiden \(y\) Werte gleich sein. Wir können -2 für \(x\) in beiden Funktionen einstecken und sicherstellen, dass die \(y\) gleich sind

\(\begin{align}3{{x}^{2}}+4&=5x+a\\3{{\left( {-2} \right)}^{2}}+4&=5\left( {-2} \right)+a\\12+4&=-10+a\\a&=26\end{align}\)

Wenn \(a=26\), ist die stückweise Funktion kontinuierlich!

Lerne diese Regeln und übe, übe, übe!

Mehr Übung: Verwenden Sie das Mathway-Widget unten, um zu versuchen, eine stückweise Funktion zu schreiben. Klicken Sie auf Senden (der blaue Pfeil rechts neben dem Problem) und klicken Sie auf Schreiben Sie den absoluten Wert stückweise, um die Antwort anzuzeigen.

Sie können auch Ihr eigenes Problem eingeben oder auf die drei Punkte in der oberen rechten Ecke klicken und auf „Beispiele“ klicken, um nach Themen zu suchen.

Wenn Sie auf Tippen klicken, um die Schritte anzuzeigen, oder hier klicken, können Sie sich bei Mathway für eine kostenlose Testversion registrieren und dann jederzeit auf ein kostenpflichtiges Abonnement upgraden (um jede Art von mathematischem Problem zu lösen!).

Weiter zu Matrizen und Lösen von Systemen mit Matrizen – Sie sind bereit!