Die Primärstruktur eines Proteins ist definiert als die Sequenz von Aminosäuren, aus denen es besteht. Diese Sequenz bestimmt letztendlich die Form, die das Protein annimmt, entsprechend den räumlichen Einschränkungen der Anordnung der Atome im Protein, den chemischen Eigenschaften der Aminosäurekomponentenreste und der Umgebung des Proteins.Die Peptidbindungen, die Aminosäurereste in einem Polypeptid verbinden, werden in einer Kondensationsreaktion zwischen der sauren Carboxylgruppe einer Aminosäure und der basischen Aminogruppe einer anderen Aminosäure gebildet. Im Zusammenhang mit einem Peptid wird die Amidgruppe (CO–NH) als Peptidgruppe bezeichnet.

Entscheidend für das Verständnis der Proteinstruktur ist die Kenntnis der Struktur der Peptidbindung. Linus Pauling untersuchte in den 1930er Jahren mit Röntgenbeugung die Art der Peptidbindung zwischen zwei Aminosäuren. Er berichtete, dass die Peptidgruppe (CO-NH) eine starre planare Struktur aufweist. Diese Struktur beruht auf Wechselwirkungen zwischen Elektronen der Doppelbindung der Carbonylgruppe und denen der C–N-Bindung (Abbildung 2), so dass letztere teilweise (etwa 40%) Doppelbindungseigenschaften erhält.

Abbildung 2 Resonanzwechselwirkungen zwischen Elektronen in der C = O–Bindung und der C-N-Bindung der Peptidgruppe bedeuten, dass Elektronen zwischen diesen Bindungen „geteilt“ werden. Beachten Sie die Ladungen an den N- und O-Atomen.

Dieser Effekt ist ein Beispiel für Resonanz, die als Austausch von Elektronen zwischen Bindungen angesehen werden kann. Da Einfachbindungen zwischen zwei Atomen länger sind als Doppelbindungen zwischen denselben zwei Atomen, unterscheiden sich die Längen der C–N- und C = O-Bindungen in der Peptidgruppe von denen, die für diese Bindungen in anderen Kontexten beobachtet wurden, in denen keine Resonanz auftritt. Somit bedeutet der partielle Doppelbindungscharakter von C–N in der Peptidgruppe, dass diese Bindung kürzer ist, als für eine C–N-Einfachbindung vorhergesagt würde, während die C = O-Bindung, die einen partiellen Einfachbindungscharakter aufgrund von Resonanz aufweist, länger ist, als für eine C = O-Doppelbindung vorhergesagt würde. Die Bindungslängen in der Peptidgruppe sind in Abbildung 3 angegeben. Vergleichen Sie die C-N-Bindung der Peptidgruppe mit der zwischen N und Ca (dem C-Atom, an das die Aminogruppe und die Carboxylgruppe gebunden sind).

Abbildung 3 Die durchschnittlichen Abmessungen in Angström, Å (10 Å = 1 nm = 1000 pm) und Grad der planaren Peptidgruppe in (a) der trans-Konformation und (b) der cis-Konformation. Hinweis: In dieser und anderen Darstellungen der Konfiguration von Polypeptiden gibt es keinen Hinweis auf die Bindungsreihenfolge (d. H. Einfach- oder Doppelbindungen).

Es gibt zwei mögliche Konformationen der planaren Peptidbindung: in der Trans-Peptidgruppe befinden sich die Ca-Atome auf gegenüberliegenden Seiten der Peptidbindung (Abbildung 3a) und in der cis-Peptidgruppe befinden sich die Ca-Atome auf derselben Seite der Peptidbindung (Abbildung 3b).

Im Allgemeinen liegen Peptidbindungen in der trans-Konformation vor. Cis-Formen können jedoch in Peptidbindungen auftreten, die einem Prolinrest vorausgehen. In solchen Fällen ist die cis-Form stabiler als üblich, da die Prolin-Seitenkette weniger hinderlich ist. Nichtsdestotrotz treten cis-Peptidbindungen nur in etwa 10% der Fälle von Peptidbindungen vor Prolinresten auf.Unter Berücksichtigung der planaren Natur der Peptidgruppe kann man sehen, dass eine Polypeptidkette ein Rückgrat hat, das aus einer Reihe starrer planarer Peptidgruppen besteht, die durch die Ca-Atome verbunden sind. Abbildung 4 zeigt einen Teil eines Polypeptids mit zwei planaren Peptidgruppen in der trans-Konformation. Beachten Sie, dass, obwohl eine Rotation um die Peptidbindungen nicht zulässig ist, ein Rotationspotential um die Ca–N– und Ca-C-Bindungen besteht. Die Drehwinkel, Torsionswinkel genannt, um diese Bindungen geben die Konformation eines Polypeptidrückgrats an. Die Torsionswinkel um die Ca–N- und Ca-C-Bindungen werden als ɸ (phi) und ψ bezeichnet. (psi) und sie sind definiert als 180 °, wenn sich das Polypeptid in der erweiterten planaren Konformation befindet, wie in Abbildung 4 dargestellt.

Abbildung 4 Ein Teil eines Polypeptids, das zwei planare Peptidgruppen (schattierte Bereiche) zeigt, die am Ca-Atom verbunden sind. Es besteht wenig Bewegungsfreiheit innerhalb der Peptidgruppe, jedoch kann eine Rotation der Peptidgruppen um die Ca–N- und Ca-C-Bindungen auftreten und wird durch die Torsionswinkel φ bzw. ψ definiert. In der hier gezeigten erweiterten Konformation sind beide Winkel als 180º definiert. Herkömmlicherweise nehmen φ und φ bei Drehung der Peptidgruppe im Uhrzeigersinn von Ca aus gesehen zu, wie durch die Pfeile angedeutet.

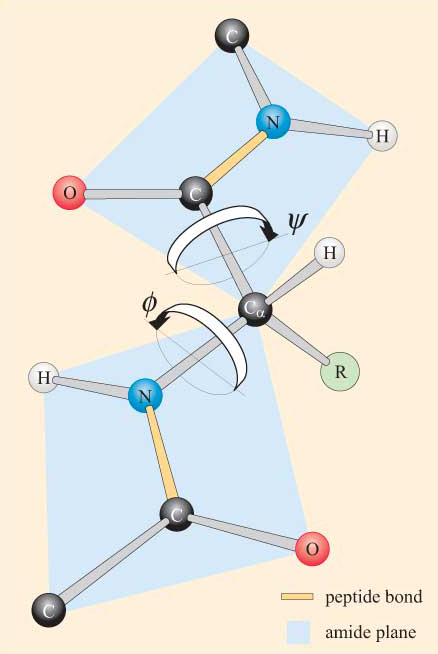
Sie werden nicht überrascht sein zu erfahren, dass sterische Einschränkungen für ɸ und ψ gelten.

Infolge dieser sterischen Einschränkungen sind nur bestimmte Werte von ɸ und ψ und damit Konformationen des Peptids zulässig, andere nicht.

Es ist möglich, diese zulässigen Werte für einen gegebenen Rest im Kontext eines Polypeptids zu berechnen. Diese Berechnung wird durchgeführt, indem zuerst die Abstände zwischen allen nichtbindenden Atomen in zwei benachbarten Peptidgruppen (wie in Abbildung 4) bei allen möglichen Werten von ɸ und ψ bestimmt werden. Es wird am leichtesten für ein Polypeptid durchgeführt, das nur eine Art von Aminosäure enthält. Ein Konformationsdiagramm von ɸ gegen ψ für einen bestimmten Rest ist als Ramachandran-Diagramm bekannt (nach seinem Erfinder, G. N. Ramachandran). Ein solches Diagramm ermöglicht es uns, diejenigen Konformationen (d. h. für einen bestimmten Wert von ɸ und ψ) zu identifizieren, die sterisch günstig oder ungünstig sind (wie in Abbildung 5), gemäß den folgenden Kriterien:

• Wo es keinen Konflikt zwischen den Van-der-Waals-Radien von nichtbindenden Atomen gibt, ist eine Konformation ‚erlaubt‘. Diese Konformationen liegen in den blauen Bereichen in Abbildung 5.

• Konformationen, die interatomare Abstände an der Grenze des Zulässigen erfordern, werden als ‚äußere Grenzkonformationen‘ definiert. Sie liegen in den Grünflächen in Abbildung 5.

• Theoretische Konformationen, die erfordern, dass zwei nicht bindende Atome näher beieinander liegen, als es ihre van-der-Waals-Radien zulassen, sind sterisch ‚verboten‘. Diese liegen in den weißen Bereichen in Abbildung 5.

Beachten Sie, dass die Werte von ɸ und ψ in Abbildung 5 von −180º bis +180º reichen. Wenn Sie die Peptidgruppe um 360º drehen, wird sie natürlich wieder in ihre Ausgangsposition gebracht, und −180º und +180º entsprechen derselben Position. Somit ist der grüne Streifen in der unteren linken Ecke des Diagramms in Abbildung 5 mit dem Feld in der oberen linken Ecke zusammenhängend.

Abbildung 5 Ein Ramachandran-Diagramm, das die sterisch zulässigen ɸ- und ψ-Winkel für eine Peptidkette zeigt, die nur l-Alaninreste enthält (Poly-l-Alanin). ‚Zulässige‘ Konformationen befinden sich innerhalb der blauen oder grünen Bereiche, wobei diejenigen, die ‚äußere Grenzkonformationen‘ sind, in letzteren liegen. Die restlichen Konformationen im weißen Bereich sind ‚verboten‘. Beachten Sie, dass es nur drei diskrete Regionen (nummeriert 1-3) gibt, die den zulässigen Konformationen entsprechen. (Daten von Ramachandran und Sasisekharan, 1968).

Ramachandran-Plots können für Polymere jeder der 20 Aminosäuren konstruiert werden. Es ist wichtig zu beachten, dass die Ramachandran-Diagramme für viele Aminosäurereste im Allgemeinen sehr ähnlich sind und nur drei Regionen mit günstigen oder tolerierten Konformationen aufweisen (in Abbildung 5 mit 1-3 im Diagramm für Poly-l-Alanin gekennzeichnet). Unterschiede treten jedoch auf. Wenn beispielsweise die Seitenkette (R in Abbildung 4) in der Nähe von Ca verzweigt ist, wie im Fall von Threonin, nimmt sie mehr Platz in der Nähe des Peptidrückgrats ein und schränkt die Annäherung von Atomen in den benachbarten Peptidgruppen ein. Infolgedessen sind zulässige Konformationen (ɸ- und ψ-Winkel) für Polypeptide verzweigter Aminosäuren eingeschränkter.

Abbildung 6 Ein Ramachandran-Diagramm für Poly-l-Glycin.Die Bereiche ‚allowed‘, ‚outer limit‘ und ‚forbidden‘ sind wie in Abbildung 5 eingefärbt. (Daten von Ramachandran und Sasisekharan, 1968)

Die Ramachandran-Diagramme in den Abbildungen 5 und 6 wurden für l-Alanin bzw. l-Glycin auf der Grundlage von zulässigen und äußeren Grenzabständen für interatomare Kontakte erstellt, die aus bekannten Werten für van-der-Waals-Radien der Atome bestimmt wurden (Tabelle 1).

Sie sind daher eher prädiktive als tatsächliche Konformationsdiagramme. Wir können natürlich Röntgenbeugung verwenden, um experimentell die ‚realen‘ Werte von ɸ und ψ für Reste in einem Polypeptid zu bestimmen. In Abbildung 7 wurden die ɸ- und ψ-Werte für alle Reste (mit Ausnahme von Glycin und Prolin) in einer Reihe verschiedener Strukturen durch hochauflösende Röntgenbeugung bestimmt und auf einem Ramachandran-Diagramm aufgetragen. Wir können sehen, dass es eine auffallende Übereinstimmung zwischen vorhergesagten und tatsächlichen Konformationen gibt. Beachten Sie jedoch, dass es einige Rückstände gibt, deren Konformationen den ‚verbotenen‘ Bereichen entsprechen. Die meisten dieser Rückstände befinden sich in der Region zwischen den ‚erlaubten‘ Regionen 2 und 3, etwa ψ = 0.

Abbildung 7 Basierend auf Röntgenbeugungsdaten für eine Reihe von Polypeptidstrukturen wurden die ɸ- und ψ-Werte für alle Aminosäurereste (mit Ausnahme von Glycin und Prolin) einem vorhergesagten Ramachandran-Diagramm der Konformationen „zulässige“ und „äußere Grenze“ überlagert. Die Vorhersagen basierten auf Van-der-Waals-Entfernungen für interatomare Kontakte, wie im Text beschrieben. Beachten Sie, dass die meisten tatsächlichen Werte den vorhergesagten zulässigen Konformationen entsprechen.

Der mit diesen Konformationen verbundene Konflikt kann durch eine geringe Verdrillung der Peptidbindung ausgeglichen werden. So wird in solchen Konformationen die Peptidgruppe aus ihrer üblichen planaren Konformation heraus verdreht.

Eine begrenzte Anzahl von ‚verbotenen‘ Konformationen bestimmter Reste kann in einem Polypeptid toleriert werden, wenn die angenommene Konformation insgesamt energetisch günstig ist. Ein Polypeptid neigt dazu, sich so zu falten, dass es die stabilste Konformation annimmt. In dieser Konformation minimiert das Polypeptid seine freie Energie. In den nächsten Abschnitten werden wir uns mit dieser höheren Ebene der Proteinstruktur befassen.