Lernziele

Am Ende dieses Abschnitts können Sie:

• Erklären Sie die potentielle Gravitationsenergie in Bezug auf die Arbeit gegen die Schwerkraft.
• Zeigen, dass die potentielle Gravitationsenergie eines Objekts der Masse m in der Höhe h auf der Erde durch PEg = mgh gegeben ist.
• Zeigen, wie die Kenntnis der potentiellen Energie als Funktion der Position verwendet werden kann, um Berechnungen zu vereinfachen und physikalische Phänomene zu erklären.

Abbildung 1. (a) Die zum Heben des Gewichts geleistete Arbeit wird im Masse-Erde-System als potentielle Gravitationsenergie gespeichert. (b) Wenn sich das Gewicht nach unten bewegt, wird diese potentielle Gravitationsenergie auf die Kuckucksuhr übertragen.

Abbildung 2. Die Änderung der potentiellen Gravitationsenergie (ΔPEg) zwischen den Punkten A und B ist unabhängig vom Pfad.

Beispiel 1. Die Kraft zu stoppen Fallen

EIN 60.0-kg Person springt aus einer Höhe von 3,00 m auf den Boden, wenn sie steif landet (wobei sich die Kniegelenke um 0,500 cm zusammendrücken), berechnen Sie die Kraft auf die Kniegelenke.

Strategie

Die Energie dieser Person wird in dieser Situation durch die Arbeit auf Null gebracht, die der Boden an ihm ausführt, wenn er anhält. Der anfängliche Stift wird in KE umgewandelt, wenn er fällt. Die Arbeit des Bodens reduziert diese kinetische Energie auf Null.

Lösung

Die Arbeit, die die Person beim Anhalten am Boden ausführt, ist durch W = Fd cos θ = −Fd mit einem Minuszeichen angegeben, da die Verschiebung beim Anhalten und die Kraft vom Boden in entgegengesetzte Richtungen gehen (cos θ = cos 180º = -1). Der Boden entfernt Energie aus dem System, so dass es negative Arbeit leistet.

Die kinetische Energie, die die Person beim Erreichen des Bodens hat, ist die Menge an potentieller Energie, die durch das Fallen durch die Höhe h verloren geht: KE = −ΔPEg = −mgh.Die Entfernung d, die die Knie der Person beugen, ist viel kleiner als die Höhe h des Sturzes, so dass die zusätzliche Änderung der potentiellen Gravitationsenergie während der Kniebeuge ignoriert wird.

Die Arbeit W, die der Boden an der Person ausführt, stoppt die Person und bringt die kinetische Energie der Person auf Null: W = −KE = mgh.

Die Kombination dieser Gleichung mit dem Ausdruck für W ergibt −Fd = mgh.

Unter Hinweis darauf, dass h negativ ist, weil die Person hingefallen ist, ist die Kraft auf die Kniegelenke gegeben durch

\displaystyle{F}=-\frac{mgh}{d}=-\frac{\left(60.0\text { kg}\rechts)\links(9.80\text { m/ s}^2\rechts)\links(-3.00\text{ m}\rechts)}{5.00\times10^{-3}\text{ m}}=3.53\times10^ 5\text{ N}\\

Diskussion

Eine so große Kraft (500 mal mehr als das Gewicht der Person) über die kurze Aufprallzeit reicht aus, um knochen brechen. Eine viel bessere Möglichkeit, den Schock abzufedern, besteht darin, die Beine zu beugen oder auf dem Boden zu rollen, wodurch die Zeit erhöht wird, über die die Kraft wirkt. Eine Biegebewegung von 0,5 m ergibt auf diese Weise eine 100-mal kleinere Kraft als im Beispiel. Das Hüpfen eines Kängurus zeigt diese Methode in Aktion. Das Känguru ist das einzige große Tier, das das Hüpfen zur Fortbewegung verwendet, aber der Schock beim Hüpfen wird durch das Biegen der Hinterbeine bei jedem Sprung abgefedert. (Siehe Abbildung 3.)

Abbildung 3. Die Arbeit, die der Boden auf dem Känguru leistet, reduziert seine kinetische Energie auf Null, wenn es landet. Durch das Aufbringen der Bodenkraft auf die Hinterbeine über eine längere Strecke wird jedoch der Aufprall auf die Knochen verringert. (kredit: Chris Samuel, Flickr)

Beispiel 2. Ermitteln der Geschwindigkeit einer Achterbahn aus ihrer Höhe

1. Wie hoch ist die Endgeschwindigkeit der in Abbildung 4 gezeigten Achterbahn, wenn sie oben auf dem 20,0 m hohen Hügel in Ruhe beginnt und die durch Reibungskräfte geleistete Arbeit vernachlässigbar ist?
2. Was ist seine Endgeschwindigkeit (wiederum unter der Annahme einer vernachlässigbaren Reibung), wenn seine Anfangsgeschwindigkeit 5,00 m / s beträgt?

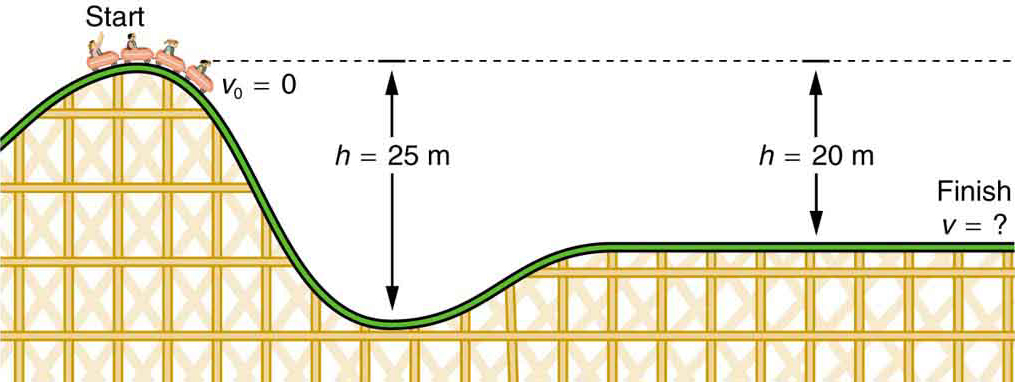
Abbildung 4. Die Geschwindigkeit einer Achterbahn nimmt zu, wenn die Schwerkraft sie bergab zieht, und ist am tiefsten Punkt am größten. Energetisch betrachtet wird die potentielle Gravitationsenergie des Achterbahn-Erde-Systems in kinetische Energie umgewandelt. Wenn die durch Reibung geleistete Arbeit vernachlässigbar ist, wird alles ΔPEg in KE umgewandelt.

Strategie

Die Achterbahn verliert potentielle Energie, wenn sie bergab fährt. Wir vernachlässigen die Reibung, so dass die verbleibende Kraft, die von der Spur ausgeübt wird, die Normalkraft ist, die senkrecht zur Bewegungsrichtung steht und keine Arbeit leistet. Die Netzarbeit auf der Achterbahn wird dann allein durch die Schwerkraft erledigt. Der Verlust der potentiellen Gravitationsenergie durch die Bewegung nach unten durch eine Entfernung h entspricht dem Gewinn an kinetischer Energie. Dies kann in Gleichungsform als −ΔPEg = ΔKE geschrieben werden. Mit den Gleichungen für PEg und KE können wir die Endgeschwindigkeit v lösen, die die gewünschte Größe ist.

Lösung für Teil 1

Hier ist die anfängliche kinetische Energie Null, so dass \Delta\text{KE}=\frac{1}{2}mv^2\\ . Die Gleichung für die Änderung der potentiellen Energie besagt, dass ΔPEg = mgh. Da h in diesem Fall negativ ist, werden wir dies als ΔPEg = −mg | h | umschreiben, um das Minuszeichen deutlich zu zeigen. Somit wird -ΔPEg = ΔKE zu mg| h/ =\frac{1}{2}{mv}^ 2\\.

Lösen für v, finden wir, dass Masse aufhebt und dass v=\sqrt{2g|h|}\\.

Ersetzen bekannter Werte,

\begin{array}{lll}v&&\sqrt{2\left(9.80\text{ m/s}^2\right)\left(20.0\text{ m}\ text{ }&&19.8\text{ m/s}\end{array}\\

Lösung für Teil 2

Wieder −ΔPEg = ΔKE. In diesem Fall gibt es anfängliche kinetische Energie, also

\Delta\text{KE}=\frac{1}{2}mv^2-\frac{1}{2}mv_0^2\\.

Somit ist mg|h/=\frac{1}{2}mv^2-\frac{1}{2}mv_0^2\\.

Umordnen ergibt \frac{1}{2}mv^2=mg|h/+\frac{1}{2}mv+0^2\\.Dies bedeutet, dass die endgültige kinetische Energie die Summe der anfänglichen kinetischen Energie und der potentiellen Gravitationsenergie ist. Masse wieder bricht, und v=\sqrt{2g|h/+v_0^2}\\.

Diese Gleichung ist der Kinematikgleichung v=\sqrt{v_0^2+2ad}\\ sehr ähnlich, aber sie ist allgemeiner — die Kinematikgleichung gilt nur für konstante Beschleunigung, während unsere obige Gleichung für jeden Pfad gilt, unabhängig davon, ob sich das Objekt mit konstanter Beschleunigung bewegt. Wenn Sie nun bekannte Werte ersetzen, erhalten Sie

\begin{array}{lll}v&&\sqrt{2\left(9.80\text{ m/s}^2\right)\left(20.0\text{ m}\right)+\left (5.00\text{ m/s}\rechts)^2}\\\text{ }&&20.4\text{ m/ s}\end{array}\\

Diskussion und Implikationen

Beachten Sie zunächst, dass mass abgebrochen wird. Dies stimmt durchaus mit Beobachtungen überein, die bei fallenden Objekten gemacht wurden, dass alle Objekte mit der gleichen Geschwindigkeit fallen, wenn die Reibung vernachlässigbar ist. Zweitens wird nur die Geschwindigkeit der Achterbahn berücksichtigt, es gibt zu keinem Zeitpunkt Informationen über ihre Richtung. Dies offenbart eine andere allgemeine Wahrheit. Wenn die Reibung vernachlässigbar ist, hängt die Geschwindigkeit eines fallenden Körpers nur von seiner Anfangsgeschwindigkeit und -höhe ab und nicht von seiner Masse oder dem eingeschlagenen Weg. Zum Beispiel hat die Achterbahn die gleiche Endgeschwindigkeit, unabhängig davon, ob sie 20,0 m gerade nach unten fällt oder einen komplizierteren Pfad wie den in der Abbildung einnimmt. Drittens, und vielleicht unerwartet, ist die Endgeschwindigkeit in Teil 2 größer als in Teil 1, aber bei weitem weniger als 5,00 m / s. Beachten Sie schließlich, dass die Geschwindigkeit in jeder Höhe auf dem Weg gefunden werden kann, indem Sie einfach den entsprechenden Wert von h am interessierenden Punkt verwenden.

Verbindungen herstellen: Untersuchung zum Mitnehmen – Umwandlung von Potential in kinetische Energie

In diesem Experiment kann die Umwandlung von potentieller Gravitationsenergie in kinetische Energie untersucht werden. Verwenden Sie auf einer glatten, ebenen Oberfläche ein Lineal mit einer Rille und einem Buch, um eine Neigung zu erzielen (siehe Abbildung 5). Legen Sie eine Murmel an der 10-cm-Position auf das Lineal und lassen Sie sie das Lineal herunterrollen. Wenn es auf die ebene Oberfläche trifft, messen Sie die Zeit, die benötigt wird, um einen Meter zu rollen. Platzieren Sie nun den Marmor an der 20-cm- und der 30-cm-Position und messen Sie erneut die Zeiten, die benötigt werden, um 1 m auf der ebenen Fläche zu rollen. Finden Sie die Geschwindigkeit des Marmors auf der ebenen Fläche für alle drei Positionen. Plotten Sie die Geschwindigkeit im Quadrat zur Entfernung, die der Marmor zurückgelegt hat. Was ist die Form jedes Grundstücks? Wenn die Form eine gerade Linie ist, zeigt das Diagramm, dass die kinetische Energie des Marmors am Boden proportional zu seiner potentiellen Energie am Freigabepunkt ist.

Abbildung 5. Ein Marmor rollt ein Lineal herunter und seine Geschwindigkeit auf der ebenen Fläche wird gemessen.

Konzeptionelle Fragen

1. In Beispiel 2 haben wir die Endgeschwindigkeit einer Achterbahn berechnet, die 20 m in der Höhe absteigt und eine Anfangsgeschwindigkeit von 5 m / s bergab hatte. Angenommen, die Achterbahn hatte stattdessen eine Anfangsgeschwindigkeit von 5 m / s bergauf gehabt, und sie rollte bergauf, hielt an und rollte dann 20 m unter dem Start zu einem Endpunkt zurück. Wir würden in diesem Fall feststellen, dass es die gleiche Endgeschwindigkeit hatte. Erklären Sie in Bezug auf die Energieeinsparung.
2. Hängt die Arbeit, die Sie an einem Buch machen, wenn Sie es auf ein Regal heben, vom eingeschlagenen Weg ab? Auf die Zeit genommen? Auf der Höhe des Regals? Über die Masse des Buches?

Probleme & Übungen

1. Ein Wasserkraftwerk (siehe Abbildung 6) wandelt die potentielle Gravitationsenergie von Wasser hinter einem Damm in elektrische Energie um. (a) Was ist die potentielle Gravitationsenergie relativ zu den Generatoren eines Sees mit Volumen 50.0 km3 (Masse = 5,00 × 1013 kg), da der See eine durchschnittliche Höhe von 40,0 m über dem Meeresspiegel hat? (b) Vergleichen Sie dies mit der Energie, die in einer 9-Megatonnen-Fusionsbombe gespeichert ist.
   

   Abbildung 6. Wasserkraftwerk (Kredit: Denis Belevich, Wikimedia Commons)

2. (a) Wie viel potentielle Gravitationsenergie (relativ zu dem Boden, auf dem es gebaut ist) ist in der Großen Pyramide von Cheops gespeichert, da seine Masse etwa 7 × 109 kg beträgt und sein Massenschwerpunkt 36 ist.5 m über dem umgebenden Boden? (b) Wie lässt sich diese Energie mit der täglichen Nahrungsaufnahme eines Menschen vergleichen?Angenommen, ein 350 g schwerer Kookaburra (ein großer Eisvogelvogel) nimmt eine 75 g schwere Schlange auf und hebt sie 2,5 m vom Boden zu einem Ast. (a) Wie viel Arbeit verrichtete der Vogel an der Schlange? (b) Wie viel Arbeit leistete sie, um ihren eigenen Schwerpunkt auf den Zweig zu heben?
3. In Beispiel 2 stellten wir fest, dass die Geschwindigkeit einer Achterbahn, die 20,0 m abgesunken war, bei einer Anfangsgeschwindigkeit von 5,00 m / s nur geringfügig größer war als beim Start aus der Ruhe. Dies impliziert, dass ΔPE >> KEi. Bestätigen Sie diese Aussage, indem Sie das Verhältnis von ΔPE zu KEi nehmen. (Beachten Sie, dass Masse storniert.)
4. Ein 100-g-Spielzeugauto wird von einer komprimierten Feder angetrieben, die es in Bewegung setzt. Das Auto folgt der Kurvenbahn in Abbildung 7. Zeigen Sie, dass die Endgeschwindigkeit des Spielzeugautos 0,687 m / s beträgt, wenn seine Anfangsgeschwindigkeit 2,00 m / s beträgt und es den reibungslosen Hang hinauffährt und 0,180 m an Höhe gewinnt.
   

   Abbildung 7. Ein Spielzeugauto fährt eine geneigte Strecke hinauf. (credit: Leszek Leszczynski, Flickr)

5. In einem Abfahrtsrennen wird überraschenderweise wenig Vorteil durch einen Laufstart gewonnen. (Dies liegt daran, dass die anfängliche kinetische Energie im Vergleich zum Gewinn an potentieller Gravitationsenergie selbst auf kleinen Hügeln gering ist.) Um dies zu demonstrieren, ermitteln Sie die Endgeschwindigkeit und die Zeit, die ein Skifahrer benötigt, der 70,0 m entlang einer 30º-Steigung fährt, wobei die Reibung vernachlässigt wird: (a) Ausgehend von der Ruhe. (b) Beginnend mit einer Anfangsgeschwindigkeit von 2,50 m / s. (c) Überrascht Sie die Antwort? Besprechen Sie, warum es immer noch vorteilhaft ist, bei sehr wettbewerbsintensiven Veranstaltungen einen Laufstart zu erzielen.

Ausgewählte Problemlösungen & Übungen

1. (a) 1,96 × 1016 J; (b) Das Verhältnis der potentiellen Gravitationsenergie im See zur in der Bombe gespeicherten Energie beträgt 0,52. Das heißt, die im See gespeicherte Energie ist ungefähr halb so hoch wie in einer 9-Megatonnen-Fusionsbombe.

3. (ein) 1.8 J; (b) 8.6 J

5. {v}_{f}=\sqrt{2}+{v_0}^2}=\sqrt{2\links(9,80\text { m/s}^2\rechts)\links(-0,180\text{ m}\rechts)+\links(2,00\text{ m/s}\rechts)^2}=0,687\text{ m/s}\\