Dies ist eine ausstehende Überarbeitung dieser Seite. Sie kann von der zuletzt akzeptierten Revision abweichen, die am 13.Januar 2011 angenommen wurde.

Das molare Volumen (Symbol Vm) eines Stoffes ist das Volumen, das ein Mol des Stoffes bei einer bestimmten Temperatur und einem bestimmten Druck einnimmt. Es ist gleich der Molekülmasse (M) der Substanz geteilt durch ihre Dichte (ρ) bei der gegebenen Temperatur und dem gegebenen Druck:

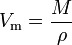
Es hat eine SI-Einheit von Kubikmetern pro Mol (m3/mol). Molare Volumina werden jedoch häufig als Kubikmeter pro 1.000 Mol (m3 / kmol) oder Kubikdezimeter pro Mol (dm3 / mol) für Gase und als Zentimeter pro Mol (cm3 / mol) für Flüssigkeiten und Feststoffe ausgedrückt.

Wenn ein Stoff ein Gemisch ist, das N Komponenten enthält, wird das Molvolumen berechnet unter Verwendung von:

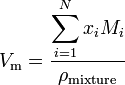
wobei x i der Molanteil der i-ten Komponente, M i die Molekülmasse der i-ten Komponente und pmischung die Mischungsdichte bei gegebener Temperatur und Druck ist.

Bei der Angabe von Molvolumenzahlen ist es wichtig, auch die gegebenen Temperatur- und Druckbedingungen anzugeben. Andernfalls sind die numerischen Werte bedeutungslos.

Ideale Gase

Die ideale Gasgesetzgleichung kann neu angeordnet werden, um diesen Ausdruck für das Molvolumen eines idealen Gases zu erhalten:

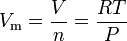
Wobei in SI-Einheiten:

= der Gasabsolutdruck, in Pa

= Molzahl, in mol

= das Gasmolarvolumen, in m3/mol

= die absolute Gastemperatur, in K

= die universelle Gasgesetzkonstante von 8,314472 m3·Pa·mol-1·K -1

Wo in US-üblichen Einheiten:

= Absolutdruck des Gases in psia

= Molzahl in lb-mol

= Molvolumen des Gases in ft3/lb-mol

= absolute Temperatur des Gases in Grad Rankine (°R)

= die universelle Gasgesetzkonstante von 10,7316 ft3·psia·lb-mol-l·°R-1

Beispielberechnungen idealer Gasmolarvolumina:

• In SI-metrischen Einheiten:

Vm = 8,314472 × 273,15 / 101,325 = 0,022414 m3/mol bei 0 ° C und 101.325 Pa Absolutdruck = 22,414 m3/kmol bei 0 °C (273,15 K) und 101.325 kPa Absolutdruck Vm = 8,314472 × 273,15 / 100.000 = 0,022711 m3/kmol bei 0 °C und 100.000 Pa Absolutdruck = 22,711 m3/kmol bei 0 °C (273,15 K) und 100 kPa Absolutdruck

• In üblichen US-Einheiten:

Vm = 10,7316 × 519,67 / 14,696 = 379,48 ft3 / lb-mol bei 60 ° F (519,67 ° R) und 14,696 psia

Anmerkungen:

• lb-mol ist eine Abkürzung für pound-mol
• ° R ist Grad Rankine (eine absolute Temperaturskala) und ° F ist Grad Fahrenheit (eine Temperaturskala).
• °R = °F + 459.67
• Die Fachliteratur kann verwirrend sein, weil einige Autoren oft nicht erklären, ob sie die universelle Gasgesetzkonstante R verwenden, die für jedes ideale Gas gilt, oder ob sie die spezifische Gasgesetzkonstante Rs verwenden, die nur für ein bestimmtes einzelnes Gas gilt. Die Beziehung zwischen den beiden Konstanten ist Rs = R / M, wobei M die Molekülmasse des Gases ist.

Reale Gase

Reale Gase sind solche Gase, die kein ideales Gasverhalten aufweisen. Für solche Gase ist die einfachste Methode zur Bestimmung des Molvolumens die Verwendung von Kompressibilitätsfaktoren wie im folgenden Ausdruck:

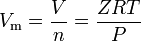
wobei Z der Gaskompressibilitätsfaktor ist, der eine nützliche thermodynamische Eigenschaft ist, um das ideale Gasgesetz zu modifizieren, um das Verhalten realer Gase zu berücksichtigen. Die obige Gleichung ist im Grunde eine einfache Zustandsgleichung (EOS). Die wesentliche Einschränkung dieser Zustandsgleichung besteht darin, dass der Gaskompressibilitätsfaktor Z keine Konstante ist, sondern von Gas zu Gas sowie mit der Temperatur und dem Druck des betrachteten Gases variiert.Genauere Werte der realen Gasmolarvolumina können durch Verwendung von Zustandsgleichungen wie der 1873 entwickelten Van-der-Waals-Gleichung, der 1949 entwickelten Redlich-Kwong-Gleichung, der 1972 entwickelten Soave-Redlich-Kwong-Gleichung und der 1976 entwickelten Peng-Robinson-Gleichung erhalten werden.

Einige Inhalte auf dieser Seite sind möglicherweise zuvor auf Citizendium erschienen.