Verwandte Seiten
Weitere Lektionen zu Mengen
Schnittpunkt zweier Mengen
Schnittpunkt von drei Mengen
Die folgenden Diagramme zeigen die Mengenoperationen und Venn-Diagramme für Komplement einer Menge, disjunkte Mengen, Teilmengen, Schnittpunkt und Vereinigung von Mengen. Scrollen Sie auf der Seite nach unten, um weitere Beispiele und Lösungen zu erhalten.
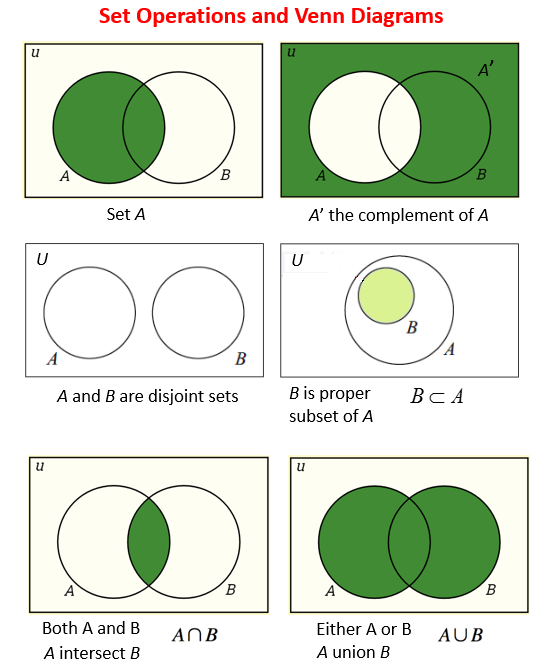
Die Menge aller betrachteten Elemente wird als Universelle Menge (U) bezeichnet und durch eine dargestelltwinkel.
- Das Komplement von A, A‘, ist die Menge der Elemente in U, aber nicht in A. A‘ ={x / x ∈ U und x ∉ A}
- Die Mengen A und B sind disjunkte Mengen, wenn sie keine gemeinsamen Elemente haben.
- B ist eine richtige Teilmenge von A. Dies bedeutet, B ist eine Teilmenge von A , aber B ≠ A.
- Der Schnittpunkt von A und B ist die Menge der Elemente in Menge A und Menge B. A ∩ B = {x | x ∈ A und x ∈ B}
- Die Vereinigung von A und B ist die Menge der Elemente in Menge A oder Gruppe B. A ∪ B = {x | x ∈ A oder x ∈ B}
- A ∩ ∅ = ∅
- A ∪ ∅ = A
- Show Video-Lektion
Set-Operationen Und Venn-Diagramme
Beispiel:
1. Erstellen Sie ein Venn-Diagramm, um die Beziehung zwischen den Mengen anzuzeigen.
U ist die Menge der ganzen Zahlen von 1 bis 15.
A ist die Menge von Vielfachen von 3.
B ist die Menge der Primzahlen.
C ist die Menge der ungeraden Zahlen.
2. Bestimmen Sie anhand des folgenden Venn-Diagramms jeden der folgenden Sätze.
a) A ∩ B
b) A ∪ B
c) (A ∪ B)‘
d) A‘ ∩ B
e) A ∪ B‘
- Video-Lektion anzeigen
Beispiel:
Die Menge P ist die Menge der geraden Zahlen zwischen 15 und 25. Zeichnen und beschriften Sie ein Venn-Diagramm zupräsentieren Sie die Menge P und geben Sie alle Elemente der Menge P im Venn-Diagramm an.
Lösung:
Listen Sie die Elemente von P auf.
P = {16, 18, 20, 22, 24} ← ‚ zwischen‘ nicht enthalten 15 und 25
Zeichnen Sie einen Kreis oder Oval. Beschriften Sie es mit P. Setzen Sie die Elemente in P.
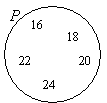
Beispiel:
Zeichnen und beschriften Sie ein Venn-Diagramm, um die Menge darzustellen
R = {Montag, Dienstag, Mittwoch}.
Lösung:
Zeichnen Sie einen Kreis oder ein Oval. Beschriften Sie es R. Setzen Sie die Elemente in R.

Beispiel:
Bei der Menge Q = { x : 2x – 3 < 11 ist x eine positive ganze Zahl }. Zeichnen und beschriften Sie ein Venn-Diagramm nachpräsentieren Sie die Menge Q.
Lösung:
Da eine Gleichung gegeben ist, müssen wir zuerst nach x lösen.
2x – 3 < 11 ⇒ 2x < 14 ⇒ x < 7
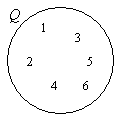
Also, Q = {1, 2, 3, 4, 5, 6}
Zeichnen Sie einen Kreis oder Oval. Beschriften Sie es mit Q.
Setzen Sie die Elemente in Q.
Venn-Diagramm Videos
Was ist ein Venn-Diagramm und was bedeuten Schnittpunkt und Vereinigung?
- Video-Lektion anzeigen
Venn-Diagramm – Zwei Teilmengen
Erfahren Sie mehr über Venn-Diagramme mit zwei Teilmengen.
- Videolektion anzeigen
Venn-Diagramm – Zwei Teilmengen unter Verwendung von Regionen
Erfahren Sie mehr über Venn-Diagramme mit zwei Teilmengen unter Verwendung von Regionen.
- Video-Lektion anzeigen
Venn-Diagramme mit drei Teilmengen
Erfahren Sie mehr über Venn-Diagramme mit drei Teilmengen.
- Video-Lektion anzeigen
Probieren Sie den kostenlosen Mathway-Rechner und Problemlöser unten aus, um verschiedene mathematische Themen zu üben. Probieren Sie die angegebenen Beispiele aus oder geben Sie Ihr eigenes Problem ein und überprüfen Sie Ihre Antwort anhand der schrittweisen Erklärungen. 