Einige interessante Dinge über Winkel und Kreise.
- Eingeschriebener Winkel
- Eingeschriebene Winkelsätze
- Beispiel: Wie groß ist der Winkel POQ? (O ist Kreismittelpunkt)
- Beispiel: Wie groß ist der Winkel CBX?
- Winkel in einem Halbkreis (Thales-Theorem)
- Ein weiterer guter Grund, warum es funktioniert
- Beispiel: Wie groß ist der Winkel BAC?
- Den Mittelpunkt eines Kreises finden
- Zyklisches Viereck
- Beispiel: Wie groß ist der Winkel WXY?
Eingeschriebener Winkel
Zunächst eine Definition:
Eingeschriebener Winkel: Ein Winkel, der aus Punkten besteht, die auf dem Umfang des Kreises sitzen.
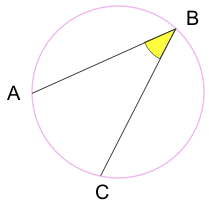
A und C sind „Endpunkte“
B ist der „Scheitelpunkt“
Spielen Sie hier damit:
Was passiert mit dem Winkel, wenn Sie den Punkt „B“ verschieben?
Eingeschriebene Winkelsätze
Ein eingeschriebener Winkel a° ist die Hälfte des zentralen Winkels 2a°
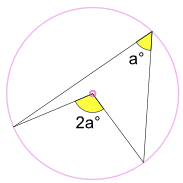
(Genannt der Winkel im Zentrumssatz)
Und (die Endpunkte fest halten) …
… der Winkel a° ist immer derselbe,
egal wo er sich auf demselben Bogen zwischen Endpunkten befindet:
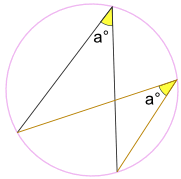
Winkel a° ist gleich.
(Genannt die Winkel, die von demselben Bogensatz subtended werden)
Beispiel: Wie groß ist der Winkel POQ? (O ist Kreismittelpunkt)
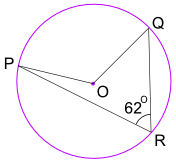
Winkel POQ = 2 × Winkel PRQ = 2 × 62° = 124°
Beispiel: Wie groß ist der Winkel CBX?
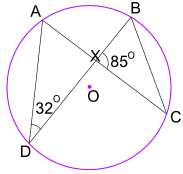
Winkel ADB = 32° entspricht auch Winkel ACB.
Und Winkel ACB ist auch gleich Winkel XCB.
Im Dreieck BXC kennen wir also den Winkel BXC = 85 ° und den Winkel XCB = 32°
Verwenden Sie nun die Winkel eines Dreiecks addieren zu 180 ° :
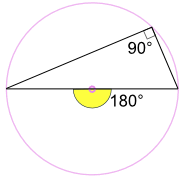
Winkel in einem Halbkreis (Thales-Theorem)
Ein Winkel, der über den Durchmesser eines Kreises eingeschrieben ist, ist immer ein rechter Winkel:
(Die Endpunkte sind beide Enden des Kreisdurchmessers,
Der Scheitelpunkt kann sich überall auf dem Umfang befinden.)
|
Warum? Da: Der eingeschriebene Winkel 90° ist die Hälfte des zentralen Winkels 180° (Mit „Winkel im Mittelpunkt Theorem“ oben) |
 |
Ein weiterer guter Grund, warum es funktioniert
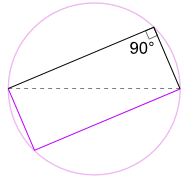
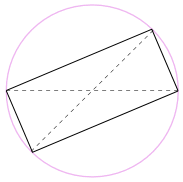
Wir könnten die Form auch um 180 ° drehen, um ein Rechteck zu erhalten!
Es ist ein Rechteck, weil alle Seiten parallel sind und beide Diagonalen gleich sind.
Und so sind seine Innenwinkel alle rechten Winkel (90 °).
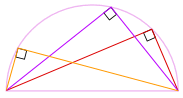
Also los geht’s! Egal wo dieser Winkel ist
auf dem Umfang ist es immer 90°
Beispiel: Wie groß ist der Winkel BAC?
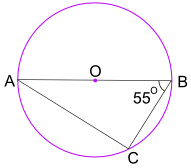
Der Winkel im Halbkreissatz sagt uns, dass der Winkel ACB = 90 ° ist
Verwenden Sie nun die Winkel eines Dreiecks addieren Sie zu 180 °, um den Winkel BAC zu finden:
Den Mittelpunkt eines Kreises finden
Mit dieser Idee können wir den Mittelpunkt eines Kreises finden:
- Zeichnen Sie einen rechten Winkel von einer beliebigen Stelle am Kreisumfang und dann den Durchmesser, an dem die beiden Beine auftreffen der Kreis
- mach das nochmal, aber für einen anderen Durchmesser
Wo sich die Durchmesser kreuzen, ist der Mittelpunkt!
Zyklisches Viereck
|
Ein „zyklisches“ Viereck hat jeden Scheitelpunkt auf dem Umfang eines Kreises: |
 |
|
Die entgegengesetzten Winkel eines zyklischen Vierecks 180 °:
|
 |
Beispiel: Wie groß ist der Winkel WXY?
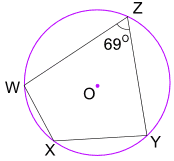
Opposite angles of a cyclic quadrilateral add to 180°

