Nach dem Verständnis der Exponentialfunktion ist unser nächstes Ziel der natürliche Logarithmus.

Wenn man bedenkt, wie das natürliche Log in mathematischen Büchern beschrieben wird, gibt es wenig „Natürliches“ daran: Es ist definiert als die Umkehrung von $ e ^ x $, ein seltsamer Exponent.

Aber es gibt eine neue, intuitive Erklärung: Das natürliche Protokoll gibt Ihnen die Zeit, die Sie benötigen, um ein bestimmtes Wachstumsniveau zu erreichen.

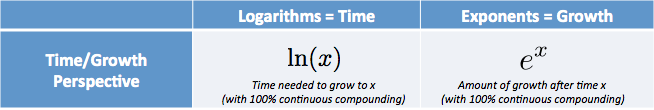
Angenommen, Sie haben eine Investition in Gummibärchen (wer nicht?) mit einem Zinssatz von 100% pro Jahr, der kontinuierlich wächst. Wenn Sie 10x Wachstum wollen, unter der Annahme einer kontinuierlichen Compoundierung, würden Sie nur $ \ ln (10) $ oder 2.302 Jahre warten. Verstehen Sie nicht, warum es nur ein paar Jahre dauert, um das 10-fache Wachstum zu erzielen? Verstehe nicht, warum das Muster nicht 1, 2, 4, 8 ist? Lesen Sie mehr über e.

e und das natürliche Protokoll sind Zwillinge:

• $ e ^ x $ ist der Betrag, den wir nach dem Start bei 1 haben.0 und wächst kontinuierlich für $ x $ Zeiteinheiten
• $\ln(x)$ (Natürlicher Logarithmus) ist die Zeit, um den Betrag $x $ zu erreichen, vorausgesetzt, wir sind kontinuierlich von 1.0 gewachsen

Nicht so schlimm, oder? Während die Mathematiker sich bemühen, Ihnen die lange, technische Erklärung zu geben, tauchen wir in die intuitive ein.

E steht für Wachstum

Die Zahl e steht für kontinuierliches Wachstum. Wie wir letztes Mal gesehen haben, können wir mit $ e ^ x $ Rate und Zeit zusammenführen: 3 Jahre bei 100% Wachstum sind dasselbe wie 1 Jahr bei 300% Wachstum, wenn es kontinuierlich zusammengesetzt wird.

Wir können eine beliebige Kombination aus Rate und Zeit (50% für 4 Jahre) verwenden und die Rate der Einfachheit halber in 100% umrechnen (was uns 100% für 2 Jahre gibt). Wenn wir auf eine Rate von 100% umrechnen, müssen wir nur an die Zeitkomponente denken:

Intuitiv bedeutet $e^x$:

• Wie wie viel Wachstum bekomme ich nach x Zeiteinheiten (und 100% kontinuierlichem Wachstum)
• Zum Beispiel: Nach 3 Zeiträumen habe ich $ e ^ 3 $ = 20,08 mal die Menge an „Zeug“.

$ e ^ x$ ist ein Skalierungsfaktor, der uns zeigt, wie viel Wachstum wir nach $ x $ Zeiteinheiten erhalten würden.

Natürlicher Logarithmus ist ungefähr Zeit

Der natürliche Logarithmus ist die Umkehrung von $ e ^ x $, ein ausgefallener Begriff für das Gegenteil. Apropos Phantasie, der lateinische Name ist Logarithmus naturali und gibt die Abkürzung ln.

Was bedeutet nun dieses umgekehrte oder entgegengesetzte Zeug?

• $ e ^x$ lässt uns die Zeit einstecken und Wachstum bekommen.
• $\ln(x)$ lässt uns das Wachstum einstecken und die Zeit bekommen, die es dauern würde.

Zum Beispiel:

• $e^3$ ist 20.08. Nach 3 Zeiteinheiten haben wir 20.08 mal was wir angefangen haben.
• $\ln(20.08)$ ist ungefähr 3. Wenn wir ein Wachstum von 20,08 wollen, würden wir 3 Zeiteinheiten warten (wiederum unter der Annahme einer kontinuierlichen Wachstumsrate von 100%).

Mit mir? Das natürliche Protokoll gibt uns die Zeit, um unser gewünschtes Wachstum zu erreichen.

Logarithmische Arithmetik ist nicht normal

Sie haben schon einmal Protokolle studiert, und sie waren seltsame Bestien. Wie wandelt man Multiplikation in Addition um? Division in Subtraktion? Mal sehen.

Was ist $\ln(1)$? Intuitiv ist die Frage: Wie lange warte ich, um 1x meinen aktuellen Betrag zu erhalten?

Null. Zip. Nada. Sie sind bereits bei 1x Ihrem aktuellen Betrag! Es braucht keine Zeit, um von 1 zu 1 zu wachsen.

• $\ln(1) = 0$

Ok, wie wäre es mit einem Bruchwert? Wie lange bekomme ich 1/2 meines aktuellen Betrags? Angenommen, Sie wachsen kontinuierlich bei 100%, wissen wir, dass $ \ ln (2) $ die Zeit ist, die verdoppelt werden muss. Wenn wir es umkehren (dh die negative Zeit nehmen), hätten wir die Hälfte unseres aktuellen Wertes.

• $\ln(.5) = – \ln(2) = -.693$

Macht Sinn, oder? Wenn wir rückwärts gehen .693 Einheiten (negative Sekunden, sagen wir) hätten wir die Hälfte unseres aktuellen Betrags. Im Allgemeinen können Sie den Bruch umdrehen und das Negativ nehmen: $ \ ln(1/3) = – \ ln(3) = -1,09 $. Das heißt, wenn wir 1,09 Zeiteinheiten zurückgehen, hätten wir ein Drittel von dem, was wir jetzt haben.

Ok, wie wäre es mit dem natürlichen Logarithmus einer negativen Zahl? Wie viel Zeit braucht es, um Ihre Bakterienkolonie von 1 auf -3 zu „wachsen“?

Es ist unmöglich! Sie können keine „negative“ Menge an Bakterien haben, oder? Am wenigsten) können Sie Null haben, aber es gibt keine Möglichkeit, eine negative Menge der kleinen Lebewesen zu haben. Negative Bakterien machen einfach keinen Sinn.

• $\ln(\text{negative number}) = \text{undefined}$

Undefined bedeutet nur „Es gibt keine Zeit, die Sie warten können“, um einen negativen Betrag zu erhalten. (Nun, wenn wir imaginäre Exponentiale verwenden, gibt es eine Lösung. Aber heute halten wir es real.)

Logarithmische Multiplikation macht mächtig Spaß

Wie lange dauert es, bis Sie das 9-fache Ihres aktuellen Betrags erreicht haben? Sicher, wir könnten einfach ln (9) verwenden. Aber das ist zu einfach, lass uns anders sein.

Wir können 9x Wachstum als Verdreifachen ($ \ ln (3) $ Zeiteinheiten) und dann wieder verdreifachen (weitere $ \ ln (3) $ Zeiteinheiten):

• Zeit zu wachsen 9x = $\ln(9)$ = Zeit zu verdreifachen und wieder zu verdreifachen = $\ln(3) + \ln(3)$

Interessant. Jede Wachstumszahl, wie 20, kann als 2x Wachstum gefolgt von 10x Wachstum betrachtet werden. Oder 4x Wachstum gefolgt von 5x Wachstum. Oder 3x Wachstum gefolgt von 6.666x Wachstum. Sehen Sie das Muster?

• $\ln(a*b) = \ln(a) + \ln(b)$

Das Protokoll von a mal b = log(a) + log(b). Diese Beziehung macht Sinn, wenn Sie in Bezug auf die Zeit denken zu wachsen.

Wenn wir 30x wachsen wollen, können wir $ \ ln (30) $ auf einmal warten oder einfach $ \ ln (3) $ warten, um zu verdreifachen, und dann $ \ ln (10) $ warten, um wieder 10x zu wachsen. Der Nettoeffekt ist der gleiche, also sollte auch die Nettozeit gleich sein (und das ist es).

Wie wäre es mit Teilung? $ \ ln (5/3) $ bedeutet: Wie lange dauert es, 5 mal zu wachsen und dann 1/3 davon zu nehmen?

Nun, 5 mal zu wachsen ist $\ln(5)$. Das Wachsen von 1/3 ist $ – \ ln (3) $ Zeiteinheiten. Also

• $\ln(5/3) = \ln(5) – \ln(3)$

Was sagt: Wachsen Sie 5 mal und „gehen Sie zurück in der Zeit“, bis Sie ein Drittel dieser Menge haben, so dass Sie mit 5/3 Wachstum übrig sind. Im Allgemeinen haben wir

• $\ln(a/b) = \ln(a) – \ln(b)$

Ich hoffe, dass die seltsame Mathematik der Logarithmen Sinn macht: multiplikation des Wachstums wird Addition der Zeit, Division des Wachstums wird Subtraktion der Zeit. Merken Sie sich die Regeln nicht, verstehen Sie sie.

Natürliche Protokolle mit jeder Rate verwenden

„Sicher“, sagen Sie, „dieses Protokollmaterial funktioniert für 100% Wachstum, aber was ist mit den 5%, die ich normalerweise bekomme?“

Es ist kein Problem. Die „Zeit“, die wir von $ \ ln () $ zurückbekommen, ist eigentlich eine Kombination aus Rate und Zeit, das „x“ aus unserer $ e ^ x $ -Gleichung. Wir nehmen nur 100% an, um es einfach zu machen, aber wir können andere Zahlen verwenden.Angenommen, wir wollen das 30-fache Wachstum: Stecken Sie $ \ ln (30) $ ein und erhalten Sie 3,4. Das bedeutet:

• $e^x = \text{growth}$
• $e^{3.4} = 30$

Und intuitiv bedeutet diese Gleichung „100% Rendite für 3.4 Jahre ist 30x Wachstum“. Wir können die Gleichung folgendermaßen betrachten:

Wir können „rate“ und „time“ ändern, solange rate * time = 3.4 . Angenommen, wir möchten das 30-fache Wachstum – wie lange warten wir unter der Annahme einer Rendite von 5%?

• $\ln(30) = 3,4$
• $\text{rate} * \text{Zeit} = 3.4$
• $.05 * \text{Zeit} = 3.4$
• $\text{Zeit} = 3.4 / .05 = 68 \text{Jahre}$

Intuitiv denke ich „$\ ln(30) = 3,4 $, also wird es bei 100% Wachstum 3,4 Jahre dauern. Wenn ich die Wachstumsrate verdopple, halbiere ich die benötigte Zeit.“

• 100% für 3,4 Jahre = 1,0 * 3,4 = 3,4
• 200% für 1,7 Jahre = 2,0 * 1,7 = 3,4
• 50% für 6,8 Jahre = 0,5 * 6,8 = 3,4
• 5% für 68 Jahre = .05 * 68 = 3,4

Cool, was? Das natürliche Protokoll kann mit jedem Zinssatz oder jeder Zeit verwendet werden, solange das Produkt gleich ist. Sie können die Variablen beliebig wackeln lassen.

Tolles Beispiel: Die Regel von 72

Die Regel von 72 ist eine mentale mathematische Abkürzung, um die Zeit zu schätzen, die benötigt wird, um Ihr Geld zu verdoppeln. Wir werden es ableiten (yay!) und noch besser, wir werden es intuitiv verstehen.

Wie lange dauert es, Ihr Geld bei 100% Zinsen zu verdoppeln, jedes Jahr zusammengesetzt?

Uh oh. Wir haben Natural Log für kontinuierliche Raten verwendet, aber jetzt fragen Sie nach jährlichen Zinsen? Wird das nicht unsere Formel durcheinander bringen? Ja, das wird es, aber bei vernünftigen Zinssätzen wie 5%, 6% oder sogar 15% gibt es keinen großen Unterschied zwischen jährlich verzinsten und vollständig kontinuierlichen Zinsen. Also die grobe Formel funktioniert, äh, grob und wir werden so tun, als ob wir völlig kontinuierliches Interesse bekommen.

Nun ist die Frage einfach: Wie lange bei 100% Zinsen verdoppeln? ln(2) = .693. Es dauert .693 Zeiteinheiten (in diesem Fall Jahre), um Ihr Geld durch kontinuierliche Aufzinsung mit einer Rate von 100% zu verdoppeln.

Ok, was ist, wenn unser Interesse nicht 100% ist, was ist, wenn es 5% oder 10% ist?

Einfach. Solange Rate * Zeit = .693, wir verdoppeln unser Geld:

• rate * time = .693
• Zeit = .693/rate

Wenn wir also nur 10% Wachstum hätten, würde es dauern .693 / .10 oder 6,93 Jahre zu verdoppeln.

Um die Dinge zu vereinfachen, multiplizieren wir mit 100, damit wir über 10 sprechen können.10:

• Zeit bis double = 69.3/rate, wobei Rate in Prozent angenommen wird.

Jetzt ist die Zeit, sich bei 5% Wachstum zu verdoppeln, 69,3 / 5 oder 13,86 Jahre. 69,3 ist jedoch nicht die am besten teilbare Zahl. Wählen wir einen nahen Nachbarn, 72, der durch 2, 3, 4, 6, 8 und viele weitere Zahlen geteilt werden kann.

• Zeit zu verdoppeln = 72/rate

das ist die Regel von 72! Leicht luftig.

Wenn Sie die Zeit zum Verdreifachen finden möchten, verwenden Sie ln(3) ~ 109.8 und erhalten

• time to triple = 110 / rate

Was eine weitere nützliche Faustregel ist. Die Regel von 72 ist nützlich für Zinssätze, Bevölkerungswachstum, Bakterienkulturen und alles, was exponentiell wächst.

Wohin von hier?

Ich hoffe, dass das natürliche Protokoll sinnvoller ist — es zeigt Ihnen die Zeit an, die für ein exponentielles Wachstum benötigt wird. Ich halte es für „natürlich“, weil e die universelle Wachstumsrate ist, also könnte ln als der „universelle“ Weg angesehen werden, um herauszufinden, wie lange es dauert, bis die Dinge wachsen.

Wenn Sie $ \ ln(x) $ sehen, denken Sie nur an „die Zeit, um auf x zu wachsen“. Im nächsten Artikel werden wir e und ln zusammenbringen, und das süße Aroma von Mathe wird die Luft füllen.

Anhang: Der natürliche Logarithmus von E

Schnelles Quiz: Was ist $\ln(e)$?

• Der mathematische Roboter sagt: Weil sie als inverse Funktionen definiert sind, eindeutig $\ln(e) = 1$
• Der intuitive Mensch: ln (e) ist die Zeit, die benötigt wird, um „e“ -Wachstumseinheiten zu erhalten (etwa 2,718). Aber e ist die Höhe des Wachstums nach 1 Zeiteinheit, also $ \ ln (e) = 1 $.

Denken Sie intuitiv.

Weitere Beiträge in dieser Serie

1. Ein intuitiver Leitfaden für Exponentialfunktionen & e
2. Entmystifizierung des natürlichen Logarithmus (ln)
3. Ein visueller Leitfaden für einfache, zusammengesetzte und kontinuierliche Zinssätze
4. Gemeinsame Definitionen von e (eingefärbt)
5. Exponenten verstehen (Warum ist 0 ^ 0 = 1?)
6. Verwendung von Logarithmen in der realen Welt
7. Wie man mit Exponenten und Logarithmen denkt
8. Diskretes vs. kontinuierliches Wachstum verstehen
9. Was bedeutet ein Exponent wirklich?
10. F: Warum ist e etwas Besonderes? (2.718…, nicht 2, 3.7 oder eine andere Zahl?)