Königsberg ist eine Stadt am Fluss Preger, die im 18. Innerhalb der Stadt befinden sich zweiwasserinseln, die mit sieben Brücken mit den Ufern verbunden sind(siehe unten).
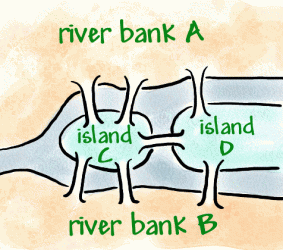
Es wurde zur Tradition, so durch die Stadt zu laufen, dass jede Brücke nur einmal überquert wurde, aber es erwies sich als schwieriges Problem. Leonhard Euler, ein Schweizer Mathematiker im Dienst vondie russische Kaiserin Katharina die Große hörte von dem Problem.1736 bewies Euler, dass der Spaziergang nicht möglich war. Erbewies dies, indem er eine Art Diagramm erfand, das als Netzwerk bezeichnet wird und aus Eckpunkten (Punkten, an denen sich Linien treffen) und Bögen (Linien) besteht.
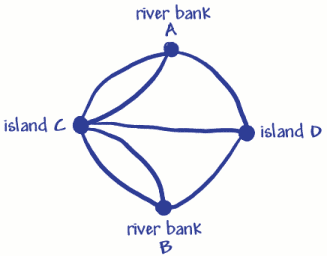
Er verwendete vier Punkte (Eckpunkte) für die beiden Flussufer und die beiden Feuchtgebiete. Diese wurden markiert A, B und C, D. Die sieben Linien(Bögen) sind die sieben Brücken. Sie können sehen, dass 3 Brücken (Bögen) mit dem Flussufer A und 3 mit dem Flussufer B verbunden sind. 5 Brücken (Bögen) verbinden sich mit Insel C und 3 verbinden sich mit Insel D. Dies bedeutet, dass alle Ecken eine ungerade Anzahl von Bögen haben, daher werden sie oddvertices genannt. (Ein gerader Scheitelpunkt müsste eine gerade Anzahl von Bögen haben).
Denken Sie daran, dass das Problem war, in der Stadt zu reisen und jede zu überquerenbrücke nur einmal. In Eulers Netzwerk bedeutete dies, jedes Zeichen nur einmal zu verfolgen und alle Scheitelpunkte zu besuchen. Euler bewies, dass es nicht möglich war, weil er herausfand, dass man, um einen ungeraden Scheitelpunkt zu haben, die Reise an diesem Scheitelpunkt beginnen oder beenden müsste. (Nachdenken).Da es nur einen Anfang und ein Ende geben kann, kann es nur zwei ungerade Eckpunkte geben, wenn Sie in der Lage sind, jedes Zeichen nur einmal zu verfolgen. Da das Brückenproblem 4 ungerade Eckpunkte hat, ist dies einfach nicht möglich! Was passiert, wenn es überhaupt keine ungeraden Eckpunkte gibt? Kann dieses Netzwerk verfolgt werden?
Die Erfindung von Netzwerken begann eine ganz neue Art von Geometrie genannttopologie. Topologie wird jetzt auf viele Arten verwendet, einschließlich für die Planungund Kartierung von Eisenbahnnetzen. (Ahhh! Züge mussten kommen….)