In anderen Abschnitten wurde erwähnt, dass viele der Eigenschaften von Feststoffen, Flüssigkeiten und Gasen erklärt werden könnten, wenn wir davon ausgehen, dass Substanzen aus Atomen oder Molekülen bestehen, die ständig in Bewegung sind. Boyles Gesetz und die anderen Gasgesetze haben uns jetzt viel mehr quantitative Informationen über Gase gegeben, und es lohnt sich zu fragen, ob wir mit dem vorherigen Modell quantitative Vorhersagen in Übereinstimmung mit diesen Gesetzen treffen können. Bei der Beantwortung dieser Frage werden wir auch wichtige Erkenntnisse über die Natur der Temperatur und der Wärmeenergie gewinnen.

Die auf Molekularbewegung basierende mikroskopische Theorie des Gasverhaltens wird als kinetische Theorie der Gase bezeichnet. Seine grundlegenden Postulate sind in Tabelle 1 aufgeführt:

TABELLE \(\pageIndex{1}\) Postulate der Kinetischen Theorie von Gasen.

1 Die Moleküle in einem Gas sind klein und sehr weit voneinander entfernt. Der größte Teil des Volumens, das ein Gas einnimmt, ist leerer Raum.

2 Gasmoleküle sind in ständiger zufälliger Bewegung. Genauso viele Moleküle bewegen sich in eine Richtung wie in jede andere.

3 Moleküle können miteinander und mit den Wänden des Behälters kollidieren. Kollisionen mit den Wänden erklären den Druck des Gases.

4 Wenn Kollisionen auftreten, verlieren die Moleküle keine kinetische Energie; das heißt, die Kollisionen sollen perfekt elastisch sein. Die gesamte kinetische Energie aller Moleküle bleibt konstant, es sei denn, es gibt eine äußere Störung der

5 Die Moleküle üben keine anziehenden oder abstoßenden Kräfte aufeinander aus, außer während des Kollisionsprozesses. Zwischen Kollisionen bewegen sie sich in geraden Linien.

Daraus kann der folgende Ausdruck für den Druck eines Gases in Bezug auf die Eigenschaften seiner Moleküle abgeleitet werden:

\ Wobei P, V = Druck und Volumen des Gases

N = Anzahl der Moleküle

m = Masse jedes Moleküls

(u2)ave = Durchschnitt (oder Mittelwert) der Quadrate aller einzelnen Molekülgeschwindigkeiten. Diese mittlere quadratische Geschwindigkeit muss verwendet werden, da der Druck proportional zum Quadrat der Molekülgeschwindigkeit ist und Molekülkollisionen dazu führen, dass verschiedene Moleküle ganz unterschiedliche Geschwindigkeiten haben.

Anstatt uns mit dem Verfahren zur Ableitung von Gl. \(\ref{1}\), lassen Sie uns die Gleichung untersuchen und sehen, dass ihre allgemeinen Merkmale so sind, wie wir es erwarten würden. In gewisser Weise ist die Fähigkeit, dies mit einer Formel zu tun, nützlicher als die Fähigkeit, sie abzuleiten. Abbildung \(\pageIndex{1}\)

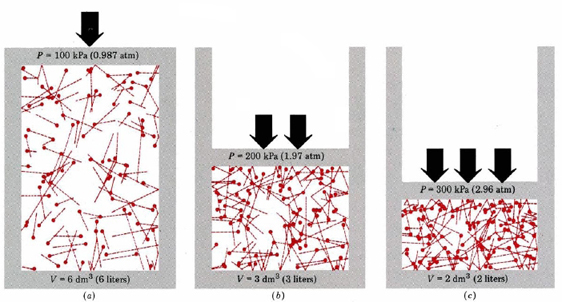Zunächst sagt uns die Gleichung, dass der Druck eines Gases proportional zur Anzahl der Moleküle geteilt durch das Volumen ist. Dies wird grafisch in Abbildung \(\pageIndex {1}\) dargestellt, wo ein Computer die gleiche Anzahl von Gasmolekülen gezeichnet hat, die jeweils drei verschiedene Volumina einnehmen. Der „Schwanz“ auf jedem Molekül zeigt den genauen Weg, dem dieses Molekül in der vorherigen Mikrosekunde gefolgt ist — je länger der Schwanz, desto schneller ging das Molekül. Der Mittelwert der Quadrate der Schwanzlängen ist proportional zu (u2)ave und in allen drei Diagrammen gleich. Es wird auch angenommen, dass alle Moleküle gleiche Massen haben.

Wie Sie sehen, erhöht die Verringerung des Gasvolumens die Anzahl der Kollisionen pro Flächeneinheit an den Wänden des Behälters. Jede Kollision übt Kraft auf die Wand aus; Kraft pro Flächeneinheit ist Druck, und so ist die Anzahl der Kollisionen pro Flächeneinheit proportional zum Druck. Die Halbierung des Volumens verdoppelt den Druck, eine Vorhersage, die mit den experimentellen Fakten übereinstimmt, die in Boyles Gesetz zusammengefasst sind. Gleichung \(\ref{1}\) besagt auch, dass der Druck proportional zur Masse jedes Gasmoleküls ist. Auch dies ist, was wir erwarten würden. Schwere Moleküle geben einen größeren „Stoß“(der Fachbegriff dafür ist Impuls) gegen die Wand als leichte mit der gleichen Geschwindigkeit.

Schließlich sagt uns die Gleichung, dass der Druck proportional zum Durchschnitt der Quadrate der Molekülgeschwindigkeiten ist. Diese Abhängigkeit vom Quadrat der Geschwindigkeit ist vernünftig, wenn wir erkennen, dass die Verdoppelung der Geschwindigkeit eines Moleküls zwei Effekte hat.

Erstens kann sich das Molekül in einer bestimmten Zeit weiter bewegen und die Anzahl der Kollisionen mit den Wänden verdoppeln. Das würde den Druck verdoppeln. Zweitens verdoppelt die Verdoppelung der Geschwindigkeit eines Moleküls den Stoß oder Impuls jeder Kollision. Dadurch verdoppelt sich der Druck wieder. Die Verdoppelung der Geschwindigkeit eines Moleküls vervierfacht daher den Druck, und für eine große Anzahl von Molekülen ist P proportional zur mittleren quadratischen Geschwindigkeit.