Boyles Gesetz
Robert Boyle (1627 – 1691), ein englischer Chemiker, gilt weithin als einer der Begründer der modernen experimentellen Wissenschaft der Chemie. Er entdeckte, dass die Verdoppelung des Drucks einer eingeschlossenen Gasprobe bei konstanter Temperatur dazu führte, dass das Volumen des Gases um die Hälfte reduziert wurde. Boyles Gesetz besagt, dass das Volumen einer gegebenen Gasmasse umgekehrt mit dem Druck variiert, wenn die Temperatur konstant gehalten wird. Eine umgekehrte Beziehung wird auf diese Weise beschrieben. Wenn eine Variable an Wert zunimmt, nimmt die andere Variable ab.
Was passiert physisch? Die Gasmoleküle bewegen sich und sind einen gewissen Abstand voneinander entfernt. Ein Druckanstieg drückt die Moleküle näher zusammen und reduziert das Volumen. Wenn der Druck verringert wird, können sich die Gase in einem größeren Volumen frei bewegen.

Mathematisch kann das Boyle-Gesetz durch die Gleichung ausgedrückt werden:
\
Das \(k\) ist eine Konstante für eine gegebene Gasprobe und hängt nur von der Masse des Gases und der Temperatur ab. Die folgende Tabelle zeigt Druck- und Volumendaten für eine eingestellte Gasmenge bei konstanter Temperatur. Die dritte Spalte stellt den Wert der Konstante \(\left( k \right)\) für diese Daten dar und ist immer gleich dem Druck multipliziert mit dem Volumen. Wenn sich eine der Variablen ändert, ändert sich die andere so, dass das Produkt aus \(P \ mal V\) immer gleich bleibt. In diesem speziellen Fall ist diese Konstante \(500 \: \text{atm} \cdot \text{mL}\).
| Pressure \(\left( \text{atm} \right)\) | Volume \(\left( \text{mL} \right)\) | \(P \times V = k\) \(\left( \text{atm} \cdot \text{mL} \right)\) |
|---|---|---|
| 0.5 | 1000 | 500 |
| 0.625 | 800 | 500 |
| 1.0 | 500 | 500 |
| 2.0 | 250 | 500 |
| 5.0 | 100 | 500 |
| 8.0 | 62.5 | 500 |
| 10.0 | 50 | 500 |
Ein Diagramm der Daten in der Tabelle veranschaulicht die inverse Beziehung des Boyle-Gesetzes (siehe Abbildung unten). Das Volumen ist auf der \(x\)-Achse aufgetragen, der entsprechende Druck auf der \(y\)-Achse.
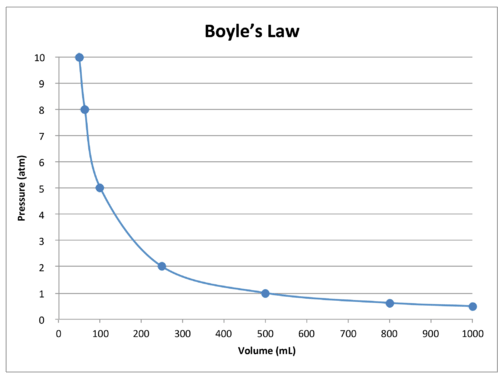
Das Boyle-Gesetz kann verwendet werden, um sich ändernde Bedingungen für ein Gas zu vergleichen. Wir verwenden \(P_1\) und \(V_1\), um für den Anfangsdruck und das Anfangsvolumen eines Gases zu stehen. Nach einer Änderung stehen \(P_2\) und \(V_2\) für den Enddruck und das Endvolumen. Die mathematische Beziehung des Boyle’schen Gesetzes lautet:
\
Diese Gleichung kann verwendet werden, um eine der vier Größen zu berechnen, wenn die anderen drei bekannt sind.
Beispiel \(\pageIndex{1}\)
Eine Probe von Sauerstoffgas hat ein Volumen von \(425 \: \text{mL}\), wenn der Druck gleich \(387 \: \text{kPa}\) ist. Das Gas wird in einen \(1,75 \: \text{L}\) Behälter expandieren gelassen. Berechnen Sie den neuen Druck des Gases.
Lösung
Schritt 1: Listen Sie die bekannten Mengen auf und planen Sie das Problem.
Bekannt
- \(P_1 = 387 \: \Text{kPa}\)
- \(V_1 = 425 \: \text{mL}\)
- \(V_2 = 1,75 \: \text{L} = 1750 \: \text{mL}\)
Unbekannt
- \( P_2 = ? \: \text{kPa}\)
Lösen Sie mit dem Boyle’schen Gesetz den unbekannten Druck \(\left( P_2 \right)\). Es ist wichtig, dass die beiden Volumina (\(V_1\) und \(V_2\)) in denselben Einheiten ausgedrückt werden, sodass \(V_2\) in \(\text{mL}\) konvertiert wurde.
Schritt 2: Lösen.
Ordnen Sie zuerst die Gleichung algebraisch neu an, um sie nach \(P_2\) zu lösen.
\
Setzen Sie nun die bekannten Größen in die Gleichung ein und lösen Sie.
\
Schritt 3: Denken Sie über Ihr Ergebnis nach.
Das Volumen hat sich auf etwas mehr als das 4-fache seines ursprünglichen Wertes erhöht und so wird der Druck um etwa ein Viertel verringert. Der Druck ist in \(\ text {kPa}\) und der Wert hat drei signifikante Zahlen. Beachten Sie, dass alle Druck- oder Volumeneinheiten verwendet werden können, solange sie während des gesamten Problems konsistent sind.