Atomic Orbitals

Ein Orbital ist die quantenmechanische Verfeinerung der Bohrschen Umlaufbahn. Im Gegensatz zu seinem Konzept einer einfachen Kreisbahn mit festem Radius sind Orbitale mathematisch abgeleitete Raumregionen mit unterschiedlichen Wahrscheinlichkeiten für ein Elektron.

Eine Möglichkeit, Elektronenwahrscheinlichkeitsverteilungen darzustellen, wurde in Abbildung 6.5.2 für das 1s-Orbital von Wasserstoff veranschaulicht. Da Ψ2 die Wahrscheinlichkeit angibt, ein Elektron in einem bestimmten Raumvolumen (z. B. einem kubischen Pikometer) zu finden, ist ein Diagramm von Ψ2 versus Entfernung vom Kern (r) ein Diagramm der Wahrscheinlichkeitsdichte. Das 1s-Orbital ist kugelsymmetrisch, so dass die Wahrscheinlichkeit, ein 1s-Elektron an einem bestimmten Punkt zu finden, nur von seiner Entfernung vom Kern abhängt. Die Wahrscheinlichkeitsdichte ist bei r = 0 (am Kern) am größten und nimmt mit zunehmender Entfernung stetig ab. Bei sehr großen Werten von r ist die Elektronenwahrscheinlichkeitsdichte sehr klein, aber nicht Null.

Im Gegensatz dazu können wir die radiale Wahrscheinlichkeit (die Wahrscheinlichkeit, ein 1s−Elektron in einem Abstand r vom Kern zu finden) berechnen, indem wir die Wahrscheinlichkeiten addieren, dass sich ein Elektron an allen Punkten auf einer Reihe von x Kugelschalen mit dem Radius r1, r2, r3, …, rx – 1, rx . Tatsächlich teilen wir das Atom in sehr dünne konzentrische Schalen, ähnlich wie die Schichten einer Zwiebel (Teil (a) in Abbildung \(\pageIndex {1}\)), und berechnen die Wahrscheinlichkeit, auf jeder Kugelschale ein Elektron zu finden. Denken Sie daran, dass die Elektronenwahrscheinlichkeitsdichte bei r = 0 am größten ist (Teil (b) in Abbildung \(\pageIndex{1}\)), so dass die Dichte der Punkte für die kleinsten Kugelschalen in Teil (a) in Abbildung \(\pageIndex{1}\) am größten ist. Im Gegensatz dazu ist die Oberfläche jeder Kugelschale gleich 4nr2, was mit zunehmendem r sehr schnell zunimmt (Teil (c) in Abbildung \(\pageIndex {1}\)). Da die Oberfläche der Kugelschalen mit zunehmendem r schneller zunimmt als die Elektronenwahrscheinlichkeitsdichte abnimmt, hat das Diagramm der Radialwahrscheinlichkeit in einem bestimmten Abstand ein Maximum (Teil (d) in Abbildung \(\pageIndex{1}\)). Am wichtigsten ist, wenn r sehr klein ist, ist die Oberfläche einer Kugelschale so klein, dass die Gesamtwahrscheinlichkeit, ein Elektron in der Nähe des Kerns zu finden, sehr gering ist; Am Kern verschwindet die Elektronenwahrscheinlichkeit (Teil (d) in Abbildung \(\ pageIndex {1}\)).

Für das Wasserstoffatom tritt der Peak im radialen Wahrscheinlichkeitsdiagramm bei r = 0,529 Å (52,9 pm) auf, was genau dem von Bohr für die n = 1-Umlaufbahn berechneten Radius entspricht. Somit ist der wahrscheinlichste Radius, der aus der Quantenmechanik erhalten wird, identisch mit dem von der klassischen Mechanik berechneten Radius. In Bohrs Modell wurde jedoch angenommen, dass sich das Elektron zu 100% in dieser Entfernung befindet, während es im quantenmechanischen Schrödinger-Modell nur einen Teil der Zeit in dieser Entfernung ist. Der Unterschied zwischen den beiden Modellen ist auf das wellenartige Verhalten des Elektrons und die Heisenbergsche Unschärferelation zurückzuführen.

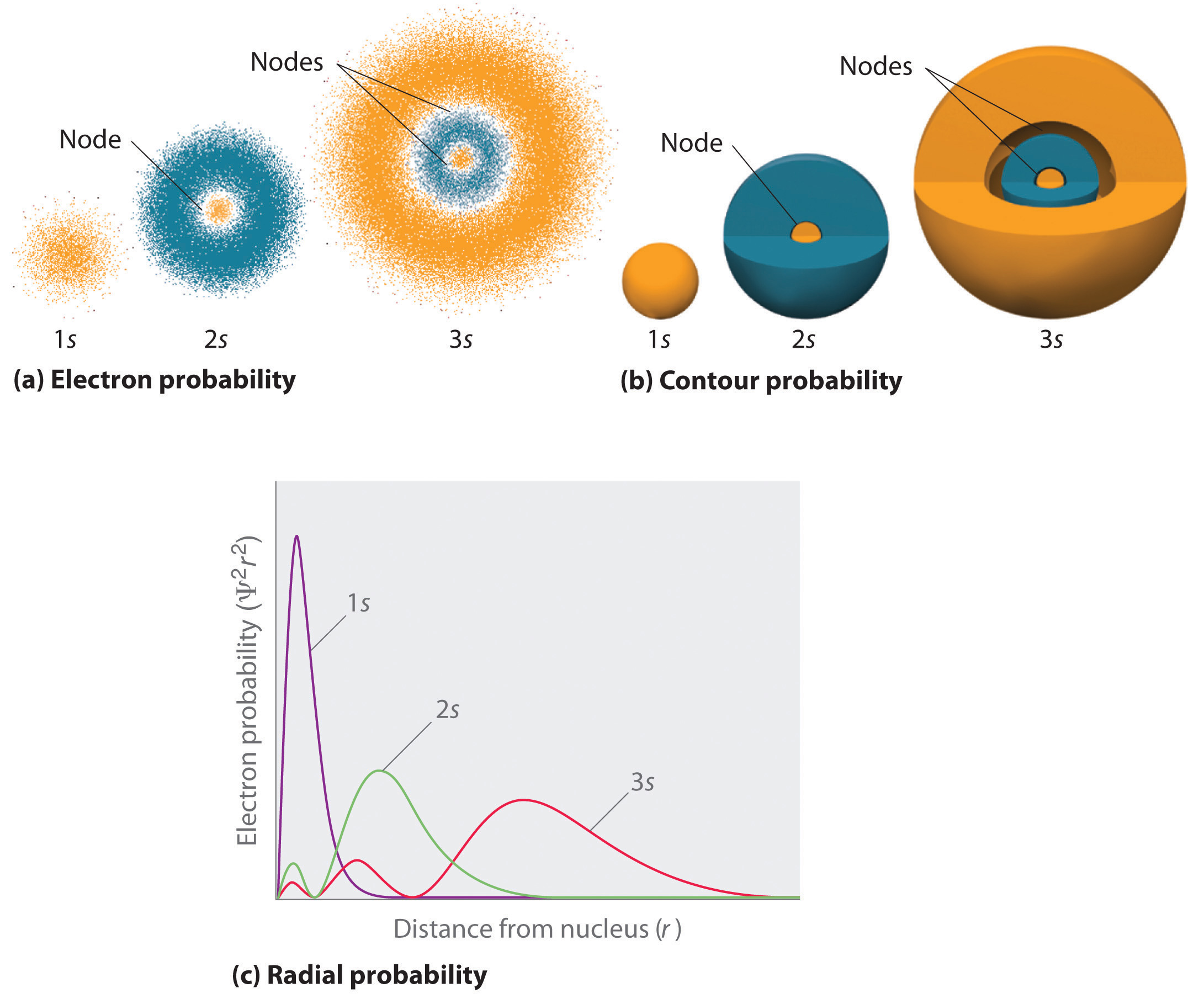
Abbildung \(\pageIndex{2}\) vergleicht die Elektronenwahrscheinlichkeitsdichten für die Wasserstofforbitale 1s, 2s und 3s. Beachten Sie, dass alle drei kugelsymmetrisch sind. Für die 2s- und 3s-Orbitale (und auch für alle anderen s-Orbitale) fällt die Elektronenwahrscheinlichkeitsdichte jedoch nicht glatt mit zunehmendem r ab. Stattdessen wird eine Reihe von Minima und Maxima in den radialen Wahrscheinlichkeitsdiagrammen beobachtet (Teil (c) in Abbildung \(\ pageIndex {2}\)). Die Minima entsprechen sphärischen Knoten (Regionen mit einer Elektronenwahrscheinlichkeit von Null), die sich mit sphärischen Regionen mit einer Elektronenwahrscheinlichkeit ungleich Null abwechseln.