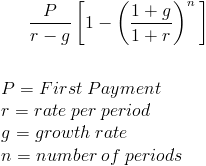
nutidsværdien af en voksende annuitetsformel beregner nutidsværdien af en række fremtidige periodiske betalinger, der vokser med en forholdsmæssig hastighed. En voksende livrente kan undertiden betegnes som en stigende livrente. Et simpelt eksempel på en voksende livrente ville være en person, der modtager $100 det første år, og successive betalinger stiger med 10% om året i alt tre år. Dette ville være en kvittering på henholdsvis $100, $110 og $121.
nutidsværdien af en voksende annuitetsformel er afhængig af begrebet tidsværdi af penge. Forudsætningen for dette koncept er, at en bestemt mængde penge er mere værd i dag end på et fremtidigt tidspunkt.
ligesom alle finansielle formler, der involverer en sats, er det vigtigt at korrelere satsen pr.periode med antallet af perioder i nutidsværdien af en voksende annuitetsformel. Hvis betalingerne er månedlige, skal satsen være den månedlige sats.
Hvordan er nutidsværdien af en voksende livrente afledt?
nutidsværdien af en voksende livrente er summen af fremtidige pengestrømme. For en voksende livrente øges hver pengestrøm med en bestemt sats. Formlen for nutidsværdien af en voksende livrente kan skrives som
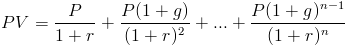
denne formel er den generelle formel til opsummering af de diskonterede fremtidige pengestrømme sammen med brug af 1 + g til faktor, idet hver fremtidig pengestrøm vil stige med en bestemt sats.
denne nutidsværdi af en voksende livrenteformel kan derefter omskrives som
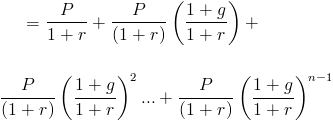
Dette ville blive betragtet som en geometrisk serie, hvor (1+g) / (1+r) er det fælles forhold. Ved at bruge den geometriske serieformel vises nutidsværdien af en voksende livrente som
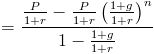
denne formel kan forenkles ved at multiplicere den med (1+r)/(1+r), som skal multiplicere den med 1. Dette annullerer mange af disse i hele formlen, hvilket efterlader
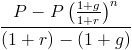
i nævneren, (1+r) – (1+g) returnerer r-G. på dette tidspunkt kan P og r-g indregnes, hvilket vil føre til nutidsværdien af en voksende livrenteformel vist øverst på siden.
vend tilbage til toppen
- formler relateret til PV af en voksende livrente
- PV af livrente
- PV af voksende Evighed
- voksende livrente-betaling (PV)
- FV af voksende livrente