några intressanta saker om vinklar och cirklar.
- inskriven vinkel
- inskrivna Vinkelsatser
- exempel: Vad är storleken på Angle POQ? (O är cirkelns centrum)
- exempel: Vad är storleken på vinkel CBX?
- vinkel i en halvcirkel (Thales ’ Theorem)
- en annan bra anledning till att det fungerar
- exempel: Vad är storleken på vinkel BAC?
- hitta en cirkels centrum
- cyklisk Fyrkant
- exempel: Vad är storleken på vinkel WXY?
inskriven vinkel
först en definition:
inskriven vinkel: en vinkel gjord av punkter som sitter på cirkelns omkrets.
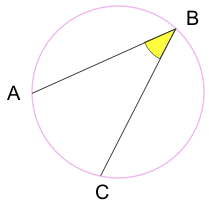
A och C är”slutpunkter ”
B är”apex point ”
spela med det här:
När du flyttar punkt” B”, Vad händer med vinkeln?
inskrivna Vinkelsatser
en inskriven vinkel a kubi är hälften av den centrala vinkeln 2a c / p >
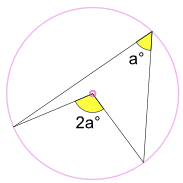
(kallad vinkeln vid Mittsatsen)
och (håller slutpunkterna fasta) …
… vinkeln a kubi är alltid densamma,
oavsett var den är på samma båge mellan slutpunkter:
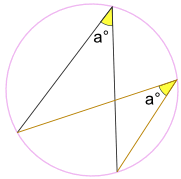
vinkel a kub är densamma.
(kallas vinklarna Subtended av samma Arc Theorem)
exempel: Vad är storleken på Angle POQ? (O är cirkelns centrum)
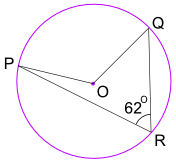
vinkel POQ = 2= 2 × 62° = 124°
exempel: Vad är storleken på vinkel CBX?
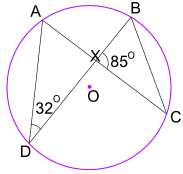
vinkel ADB = 32 kg motsvarar också vinkel ACB.
och vinkel ACB är också lika med vinkel XCB.
så i triangel BXC vet vi vinkel BXC = 85 kg, och vinkel XCB = 32 kg
använd nu vinklar av en triangel Lägg till 180 kg :
vinkel i en halvcirkel (Thales ’ Theorem)
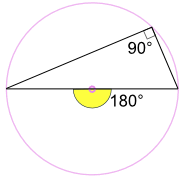
en vinkel inskriven över en cirkels diameter är alltid en rät vinkel:
(ändpunkterna är vardera änden av en cirkels diameter,
spetsen punkten kan vara var som helst på vänster sida omkrets.)
|
varför? Eftersom: den inskrivna vinkeln 90 kg är hälften av den centrala vinkeln 180 kg (med hjälp av ”vinkel vid Mittsatsen” ovan) |
 |
en annan bra anledning till att det fungerar
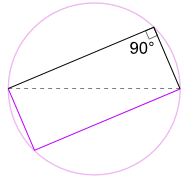
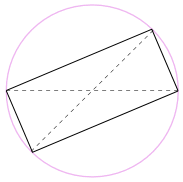
vi kan också rotera formen runt 180 kg för att göra en rektangel!
det är en rektangel, eftersom alla sidor är parallella och båda diagonalerna är lika.
och så är dess inre vinklar alla rätvinklar (90 kg).
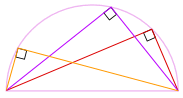
så där går vi! Oavsett var den vinkeln är
på omkretsen, är det alltid 90 kg
exempel: Vad är storleken på vinkel BAC?
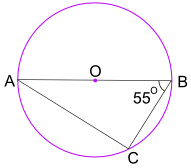
vinkeln i Halvcirkelsatsen berättar att vinkeln ACB = 90:
hitta en cirkels centrum
Vi kan använda den här tanken för att hitta en cirkels centrum:
- rita en rät vinkel var som helst på cirkelns omkrets, dra sedan diametern där de två benen träffar cirkeln
- gör det igen men för en annan diameter
där diametrarna korsar är mitten!
cyklisk Fyrkant
|
en ”cyklisk” Fyrkant har varje toppunkt på en cirkels omkrets: |
 |
|
en cyklisk quadrilateral motsatta vinklar Lägg till 180 kg:
|
exempel: Vad är storleken på vinkel WXY?
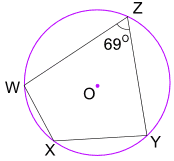
Opposite angles of a cyclic quadrilateral add to 180°


