detta avsnitt täcker:
- introduktion till bitvis funktioner
- utvärdera bitvis funktioner
- grafera bitvis funktioner
- hur man berättar om en bitvis funktion är kontinuerlig eller icke-kontinuerlig
- erhålla ekvationer från bitvis funktionsgrafer
- absolut värde som en bitvis funktion
- transformationer av bitvis funktioner
- bitvis funktion ordproblem
- mer övning

bitvis funktioner (eller bitvisa funktioner) är precis vad de heter: delar av olika funktioner (underfunktioner) allt på en graf. Det enklaste sättet att tänka på dem är om du ritade mer än en funktion på en graf och du bara raderade delar av funktionerna där de inte ska vara (längs \(x\)’s); de definieras annorlunda för olika intervall på \(x\). \(y\) definieras annorlunda för olika värden på \(x\); vi använder \(x\) för att leta upp vilket intervall det är i, så vi kan ta reda på vad \(y\) ska vara.
Observera att det finns ett exempel på en bitvis funktion inverse här i avsnittet Inverses of Functions.
Here’s an example and graph:
|
Piecewise Function |
Graph |
|
\(\displaystyle f\left( x \right)=\left\{ \begin{align}2x+8\,\,\,\,\,&\text{ if }x\le -2\\{{x}^{2}}\,\,\,\,\,\,\,\text{ }\,&\text{ if }x>-2\end{align} \right.\) (det finns andra sätt att visa detta, till exempel att använda ett ”för” istället för ett ”om”, och använda kommatecken eller halvkolon istället för ”om”.) domän: \(\mathbb{R},\,\,\,\text{eller}\,\,\vänster( {-\infty ,\infty } \höger)\) intervall: \(\mathbb{R},\,\,\,\text{eller}\,\,\vänster( {-\infty ,\infty } \höger)\) |
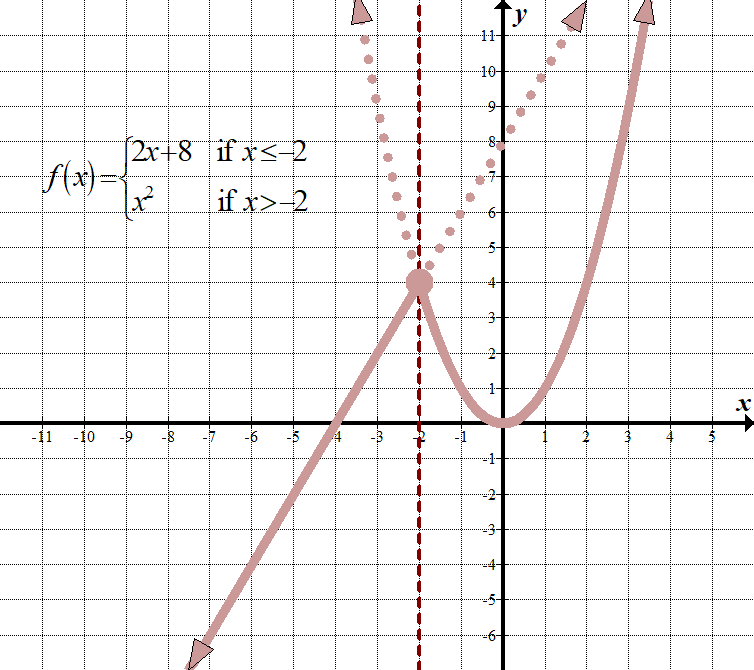 |
vad detta betyder är för varje \(x\) mindre än eller lika med -2, vi måste rita linjen \(2x+8\), som om det var den enda funktionen i diagrammet. För varje\ (x\) värde större än -2 måste vi graf\ ({{x}^{2}}\), som om det var den enda funktionen i diagrammet. Då måste vi ”bli av med” de delar som vi inte behöver. Kom ihåg att vi fortfarande använder ursprunget som referenspunkt för båda graferna!
se hur den vertikala linjen \(x=-2\) fungerar som en ”gräns” linje mellan de två graferna?
Observera att punkten \((-2,4)\) har en sluten cirkel på den. Tekniskt sett bör den bara tillhöra funktionen \(2x+8\), eftersom den funktionen har mindre än eller lika tecken, men eftersom punkten också finns på grafen \({{x}^{2}}\) kan vi bara använda en sluten cirkel som om den visas på båda funktionerna. Inte så illa, eller hur?
utvärdera bitvis funktioner
Ibland får du bitvis funktioner och uppmanas att utvärdera dem; med andra ord, hitta \(y\) – värdena när du får ett \(x\) – värde. Låt oss göra detta för \(x=-6\) och \(x=4\) (utan att använda grafen). Här är funktionen igen:
\(\displaystyle f \ left (x \right)= \ left\ {\begin{align}2x+8\,\,\,\,\,&\text{ if }x \ le -2\ \ {{x}^{2}}\,\,\,\,\,\,\,\text { }\, &\text{ if }x>-2\end{align} \right.\)
vi vill först titta på villkoren till höger först för att se var vår \(x\) är. När \(x=-6\) vet vi att det är mindre än -2, så vi kopplar bara in vår \(x\) till \(2x+8\). \(f (x)\) eller \(y\) är \((2)(-6)+8=-4\). Vi bryr oss inte ens om \(\boldsymbol{{x}^{2}}\)! Det är så enkelt. Du kan också se att vi gjorde detta korrekt genom att använda grafen ovan.
försök nu \(x=4\). Vi tittar först till höger och ser att vår \(x\) är större än -2, så vi ansluter den till \({{x}^{2}}\). (Vi kan bara ignorera \(2x + 8\) den här gången.) \(f(x)\) eller \(y\) är \({{4}^{2}}=16\).
grafera bitvis funktioner
Du kommer förmodligen att bli ombedd att grafera bitvis funktioner. Ibland innehåller graferna funktioner som inte är kontinuerliga eller diskontinuerliga, vilket innebär att du måste plocka upp din penna mitt i grafen när du ritar den (som ett hopp!). Kontinuerliga funktioner innebär att du aldrig behöver plocka upp din penna om du skulle dra dem från vänster till höger.
och kom ihåg att graferna är sanna funktioner endast om de passerar det vertikala linjetestet.
låt oss rita dessa bitvis funktioner och avgöra om de är kontinuerliga eller icke-kontinuerliga. Observera hur vi ritar varje funktion som om den var den enda, och sedan ”radera” de delar som inte behövs. Vi får också domänen och intervallet som vi gjorde här i avsnittet algebraiska funktioner.
| Piecewise Function | Graph |
|
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-2x+8\,\,\,\,\,\,\text{if }x\le 4\\\frac{1}{2}x-2\,\,\,\,\,\,\,\,\,\text{if }x>4\end{array} \right.\) Continuous Domain: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) Range: \(\left( {0,\infty } \right)\) |
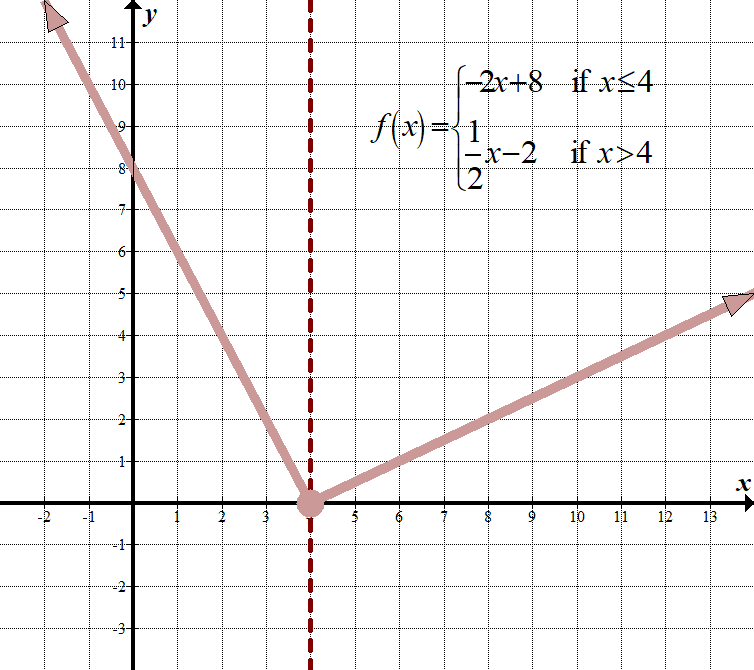 |
|
\(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\,\text{if }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1}\le x<4\\x-5\,\,\,\,\,\,\,\,\,\text{if }x\ge 4\end{array} \right.\) Non-Continuous Domain: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) Range: \(\mathbb{R},\,\,\,\text{or}\,\,\left( {-\infty ,\infty } \right)\) |
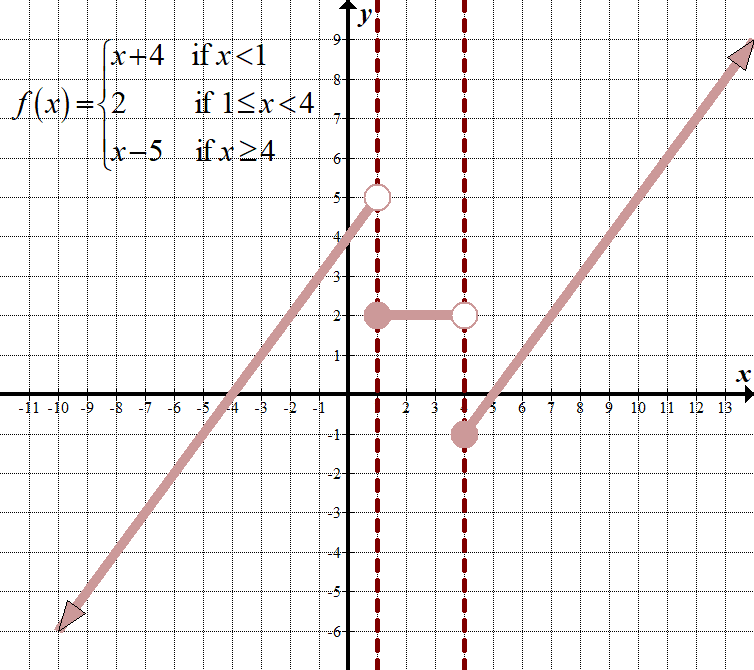 |
We can actually put piecewise functions in the graphing calculator:
| Piecewise Function Screens | Steps and Notes |
| Enter the piecewise function on three lines:
här är grafen:
|
för att sätta bitvis funktionen \(\displaystyle f\left( x \right)=\left\{ \begin{array}{L}x+4\,\,\,\,\,\,\,\,\,\text{if }x <1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1} \ le x < 4\ \ -5 + x\,\,\,\,\,\text{if }x \ ge 4\end{array} \ höger.\ ) i räknaren kan du ange funktionen på tre rader genom att dividera funktionen i varje intervall med en ”test ojämlikhet” av det intervallet (och titta på parenteser!).
anledningen till att vi delar med intervaller eller ojämlikheter är att räknaren returnerar en 1 om ojämlikheten(som \(x<1\)) är sant; till exempel kommer \((x+4)\) bara att hamna \((x+4)/(1)\) När \(x<1\). När \(x \ ge 1\) delar vi med 0, så ingenting kommer att dras. Här är vad vi kan lägga i räknaren: \(\displaystyle \begin{array}{l}{{Y}_{1}}=\vänster( {x+4} \höger)/\vänster( {x<1} \höger)\\{{Y}_{2}}=\vänster( 2 \höger)/\vänster( {X\ge 1\text{ och }X<4} \right)\\{{y}_{3}}=\Left( {-5+x} \right)/\left( {x\ge 4} \right)\end{array}\) (Observera att du också kan ange detta på en rad genom att multiplicera villkoren istället för att dela och använda plustecken mellan var och en av de tre funktionerna/intervallen: \(\displaystyle {{Y}_{1}}=\vänster( {x+4} \höger)\vänster( {x<1} \höger)+\vänster( 2 \höger)\vänster( {x\ge 1\text{ och }x<4} \höger)+\vänster( {-5+x} \höger)\vänster( {x\ge 4} \höger)\).) här är tangenttryckningarna för att använda tre rader. Observera att du använder 2nd MATH (TEST) för att komma till skärmen som har \(\le \), \(\ge\) och så vidare. Till exempel får 2: a MATH 6 dig \(\le \). Använd 2: a matematik (TEST), rätt till logik, sedan 1, för ”och” i \({{Y}_{2}}\).
|
2 kan titta på gränspunkterna och se om \(y\) punkten är densamma vid var och en av dem. (Om \(y\) var annorlunda skulle det finnas ett ”hopp” i grafen!)
låt oss prova detta för de funktioner vi använde ovan:
| Piecewise Function | Check Boundary Points |
| \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}-2x+8\,\,\,\,\,\,\,\text{if }x\le 4\\\frac{1}{2}x-2\,\,\,\,\,\,\,\,\,\,\text{if }x>4\end{array} \right.\) | Let’s check \(x=4\) in both parts of the function, since 4 is the ”boundary point”:
\(\begin{array}{l}-2(4)+8=0\\\,\,\,\frac{1}{2}(4)-2=0\end{array}\) eftersom \(0=0\) är denna bitvis funktion kontinuerlig. |
| \(\displaystyle f\vänster( x \höger)= \ vänster \ {\begin{array}{l}x+4\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if }x <1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1} \ le x < 4\ \ -5 + x\,\,\,\,\,\,\,\,\,\text{if }x \ ge 4\end{array} \ höger.\ ) | låt oss kolla in de två första delarna av funktionen. I den andra delen är \(y\) alltid 2:
\(\begin{array}{l}1+4=5\\\,\,\,\,\,\,\,\,\,2=2\end{array}\) sedan \(5\ne 2\) kan vi stanna här och notera att denna bitvis funktion är icke-kontinuerlig. Om \(y\) var lika, måste vi gå en för att kontrollera nästa Gränspunkt vid \(x=4\). |
hämta ekvationer från bitvis funktionsgrafer
Du kan bli ombedd att skriva en bitvis funktion, givet en graf. Nu när vi vet vilka bitvis funktioner handlar om är det inte så illa!
för att granska hur man får ekvationer från linjära grafer, se erhålla ekvationerna för en linje, och från quadratics, se Hitta en kvadratisk ekvation från punkter eller en graf.
här är graferna, med förklaringar om hur man härleder sina bitvis ekvationer:
| Piecewise Function Graph | Procedure to get Function |
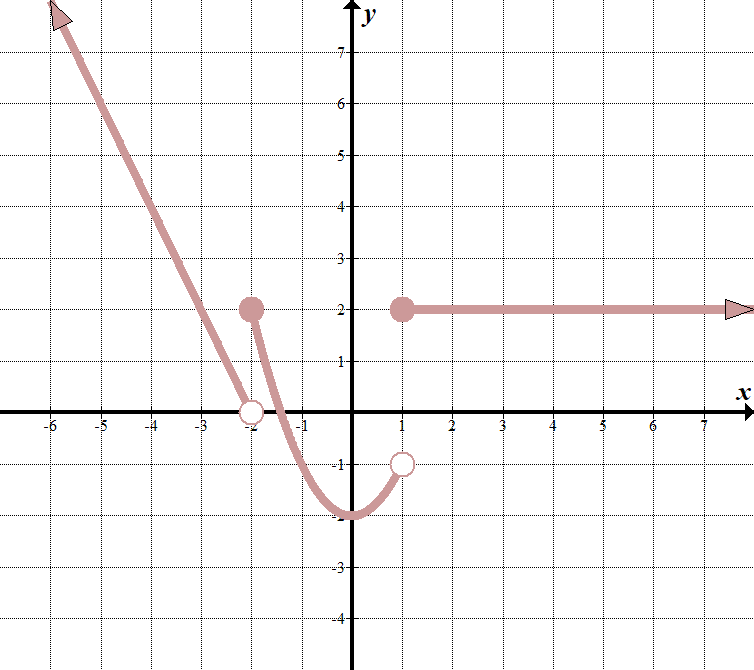 |
We see that our ”boundary lines” are at \(x=-2\) and \(x=1\). We know that our function will look something like this (notice open and closed endpoints):
\(\displaystyle f \ vänster (x \ höger)= \ vänster \ {\begin{array}{l}\text{ }……\,\,\,\,\,\,\,\,\text{if }x < -2 \ \ \ text{ }……\,\,\,\,\,\,\,\,\text{if } – \text{2 } \ Le x < 1 \ \ \ text{ }……\,\,\,\,\,\,\,\,\text{if }x \ ge 1\end{array} \ höger.\ ) Vi kan välja två punkter \((-2,0)\) och \((-3,2)\) på den vänstra raden för att få ekvationen \(y=-2x-4\). mittfunktionen är \(y={{x}^{2}}-2\), och funktionen längst till höger är bara den horisontella linjen \(y=2\). således är den bitvis funktionen: \(\displaystyle f \ vänster (x \ höger)= \ vänster \ {\begin{array}{l} – 2x-4\,\,\,\,\,\,\,\text{if }x < -2\ \ \ text { } {{x}^{2}}-2\,\,\,\,\,\,\,\,\,\,\text{if } – \text{2} \ Le x < 1 \ \ \ text{ 2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if }x \ ge 1\end{array} \ höger.\) |
 |
vi ser att vår ”gränslinje” är vid \(x=5\). Eftersom linjerna möts vid \((5,4)\) spelar det ingen roll var vi sätter tecknet \(\le \) eller \(\ge \) ; vi kan bara inte sätta det båda platserna, annars skulle det inte vara en funktion. Vi har hittills:
\(\displaystyle f \ left (x \right)= \ left \ {\begin{array}{l} \ text{ }……\,\,\,\,\,\,\,\,\,\text{if }x < 5 \ \ \ text{ }……\,\,\,\,\,\,\,\,\,\text{if }x \ ge 5\end{array} \ höger.\ ) återigen måste vi titta på varje rad separat för att bestämma deras ekvationer. Vi kan antingen ta 2 poäng från varje rad för att få dessa, eller härleda från backar och\(y\)–avlyssningar; den bitvis funktionen är: \(\displaystyle f \ vänster (x \ höger)= \ vänster \ {\begin{array}{l} \ frac {6}{5}x-2\,\,\,\,\,\,\,\text{if }x < 5\ \ \ frac{2}{5}x+2\,\,\,\,\,\,\,\text{if }x \ ge 5\end{array} \ höger.\) |
absolutvärde som en bitvis funktion
Vi kan skriva absolutvärdefunktioner som bitvis funktioner – det är riktigt coolt! Du kanske vill granska lösningen av absoluta Värdeekvationer och ojämlikheter innan du fortsätter till detta ämne.låt oss säga att vi har funktionen \(f\left (x \right)=\left| x \right|\). Från vad vi lärde oss tidigare vet vi att när \(x\) är positivt, eftersom vi tar det absoluta värdet, kommer det fortfarande bara att vara \(x\). Men när \(x\) är negativt, när vi tar det absoluta värdet, måste vi ta det motsatta (negera det), eftersom det absoluta värdet måste vara positivt. Vettigt? Så, till exempel, om vi hade \(|5|\), tar vi bara vad som finns i det absoluta tecknet, eftersom det är positivt. Men för \(|-5/\) måste vi ta motsatsen (negativ) av vad som finns inom det absoluta värdet för att göra det \(\displaystyle 5\,\,\,(-\,-5=5)\).
det betyder att vi kan skriva denna absoluta värdefunktion som en bitvis funktion. Lägg märke till att vi kan få ”vändpunkten” eller ”gränspunkten” genom att ställa in vad som ligger inom absolutvärdet till 0. Då använder vi antingen den ursprungliga funktionen eller negerar funktionen, beroende på funktionens tecken (utan absolut värde) i det intervallet.
Vi kan till exempel skriva \(\displaystyle \ left / x \ right / \ text { } = \ left \ {\begin{array}{l}x\,\,\,\,\,\,\,\,\,\text{if }x \ ge 0\\ – x\,\,\,\,\,\text{if }x<0\end{array} \right.\). Observera också att om funktionen är kontinuerlig (det finns inget ”hopp”) vid gränspunkten spelar det ingen roll var vi sätter ”mindre än eller lika med” (eller ”större än eller lika med”) tecken, så länge vi inte upprepar dem! Vi kan inte upprepa dem eftersom vi teoretiskt sett inte kan ha två värden på \(y\) för samma \(x\), eller vi skulle inte ha en funktion.
Here are more examples, with explanations. (You might want to review Quadratic Inequalities for the second example below):
| Absolute Value Function | Method to get Piecewise Function |
| \(g\left( x \right)=\left| {2x+3} \right|\) | Let’s first find the ”boundary line”. Vi gör detta genom att ställa in vad som finns inom det absoluta värdet till 0 och sedan lösa för \(\boldsymbol{x}\).
När \(2x+3\ge 0\) får vi \(\displaystyle x\ge -\frac{3}{2}\) (faktiskt kan vi behålla \(\ge \) när vi löser). När \(2x+3\) är positivt tar vi det bara ”som det är”, men om det är negativt måste vi negera hela saken. därför är funktionen bitvis: \(\displaystyle \ vänster / {2x + 3} \ höger / =\vänster \ {\begin{array}{l}2x+3\,\,\,\,\,\,\,\,\,\text{if }x \ ge – \ frac{3}{2} \ text { } \\ – 2x-3\,\,\,\,\,\text{if }x<-\frac{3}{2}\end{array} \right.\) prova det-det fungerar! |
| \(f\left( x \right)=\left| {{{x}^{2}}-4} \right|\) | låt oss först hitta” gränslinjen(er)”; vi ställer in vad som finns inuti det absoluta värdet till 0.
När \({{x}^{2}}-4 \ ge 0\) får vi \(x\le -2\) eller \(x\ge 2\) (prova några siffror!). När \({{x}^{2}}-4\) är positivt tar vi det bara ”som det är”, men om det är negativt måste vi negera det. funktionen bitvis är: \(\displaystyle \ left / {{{x}^{2}}-4} \ right / =\left \ {\begin{array}{l}{{x}^{2}}-4\,\,\,\,\,\text{if }x \ le -2\ \ 4 – {{x}^{2}}\,\,\,\,\,\text{if }-2< x < 2\ \ {{x}^{2}}-4\,\,\,\,\,\text{if }x \ ge 2\text { } \ end{array} \ right.\ ) eller \(\displaystyle \ vänster / {{{x}^{2}}-4} \ höger / = \ vänster\ {\begin{array}{l}{{x}^{2}}-4\,\,\,\,\,\,\text{if }x \ le -2\text { }\,\, \ text{eller}\,\, \ text{ }x \ ge 2 \ \ 4 – {{x}^{2}}\,\,\,\,\,\,\,\text{if }-2<x<2\end{array} \höger.\) igen (eftersom funktionen är kontinuerlig) spelar det ingen roll var vi har \(\le\) och \(\ge\) (i motsats till \(<\) och \(>\)), så länge vi inte upprepar dem. |
| \(f\left( x \right)=2x+\left| {x+2} \right|\) | den här är lite svårare, eftersom vi har en \(x\) inuti och utanför det absoluta värdet. För ”gränslinjen” använder vi bara det som ligger inom det absoluta värdet.
När \(x + 2\ge 0\) får vi \(x\ge -2\). Men för den bitvis funktionen måste vi använda hela funktionen, inklusive den del som ligger utanför absolutvärdet. Så, den bitvis funktionen är: \(\displaystyle 2x+ \ vänster / {x + 2} \ höger / = \ vänster \ {\begin{array}{l}2x + x+2\,\,\,\,\,\text{if }x \ ge -2\ \ 2x-x-2\,\,\,\,\,\text{if }x <-2\end{array} \höger.\) låt oss förenkla: \(\displaystyle 2x+\vänster|{x+2} \höger / =\vänster \ {\begin{array}{l}3x+2\,\,\,\,\,\,\,\text{if }x \ ge -2\ \ x-2\,\,\,\,\,\,\,\,\,\,\text{if }x <-2\end{array} \höger.\ ) prova några värden mindre än och bra då -2; de borde fungera! |
| \(g \ left (x \ right)= \ left| {{{x}^{2}}-4x-5} \ right/\) | den här löses bäst med ett teckendiagram eftersom vi har en kvadratisk och vi behöver veta var funktionen är positiv och negativt.
först, faktor kvadratiska inuti absolutvärdet funktionen till \(\vänster ({x-5}\höger) \vänster ({x+1}\höger)\). Använd sedan ett teckendiagram för att se var faktorerna är positiva och negativa, och kom ihåg att där faktorerna är positiva använder vi funktionen ”som den är” och där faktorerna är negativa negerar vi funktionen: \(\displaystyle \ vänster / {{{x}^{2}} – 4x-5} \höger / =\vänster \ {\begin{array}{l}{{x}^{2}} – 4x-5\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if }x \ le -1\,\,\,\,\text{eller}\,\,\,\, x\ge 5\ \ – \ vänster ({{{x}^{2}} – 4x-5} \höger)\,\,\,\,\text{if }-1<x<5\text{ }\end{array} \right.\) |
| \(\displaystyle g\vänster( x \höger)=\frac{{\vänster| {x+2} \höger|}}{{x+2}}\) | detta är en rationell funktion, eftersom det finns en variabel i nämnaren.
När \(x + 2\ge 0\) får vi \(\displaystyle x\ge -2\). När \(x + 2\) är positivt tar vi det bara ”som det är”, men om det är negativt måste vi negera vad som finns i det absoluta värdet: \(\displaystyle \ frac {{\left / {x + 2} \ right/}} {{x + 2}}= \ left\ {\begin{array}{l} \ frac {{x + 2}}{{x+2}}\,\,\,\,\,\,\,\,\,\text{if }x \ ge -2\\\frac {{- x-2}}{{x+2}}\,\,\,\,\,\,\text{if }x <-2\end{array} \höger.\). Men vi måste vara försiktiga, eftersom \(x\ne 2\) (domänbegränsning: nämnaren skulle vara 0). därför är funktionen bitvis: \(\displaystyle \ frac {{\left / {x + 2} \ right/}} {{x + 2}}= \ left\ {\begin{array}{l}1\,\,\,\,\,\,\,\,\,\,\text{if }x >-2\\-1\,\,\,\,\,\,\text{if }x <-2\end{array} \höger.\). |
Du kan också bli ombedd att ta ett absolut värdegraf och skriva det som en bitvis funktion:
| Absolute Value Graph | Method to get Piecewise Function |
 |
We see that our ”boundary line” is at \(x=0\), so what’s inside the absolute value sign must be \(x\) or a factor of \(x\). (Detta beror på att för att få gränslinjen med en absolut värdefunktion ställer vi in vad som finns inom absolutvärdet till 0 och löser för \(x\)).
När \(x >0\) kan vi se att ekvationen för linjen är \(y=2x-2\). När \(x<0\) är ekvationen \(y=2x-2\). Vi kan skriva detta som en bitvis funktion: \(\displaystyle f\left (x \ right)= \ left \ {\begin{array}{l}2x-2\,\,\,\,\,\,\,\text{if }x>0\\-2x-2\,\,\,\text{if }x\le 0\end{array} \right.\) Vi kan också skriva detta som en transformerad absolutvärdesfunktion: \(y=2\left| x \right|-2\) eller \(y=\left| {2x} \right|-2\) (eftersom 2 är positivt kan det vara inuti eller utanför \(\left| { \ ,\,} \right|\)). (Det här är meningsfullt eftersom när det som finns inuti \(\left| {\,\,} \right|\) är \(> 0\) använder vi den vanliga funktionen \(y=2x-2\), och när det som finns inuti är \(< 0\), negerar vi den absoluta värdedelen för att göra den \(y=-\left ({2x} \höger)-2\)). |
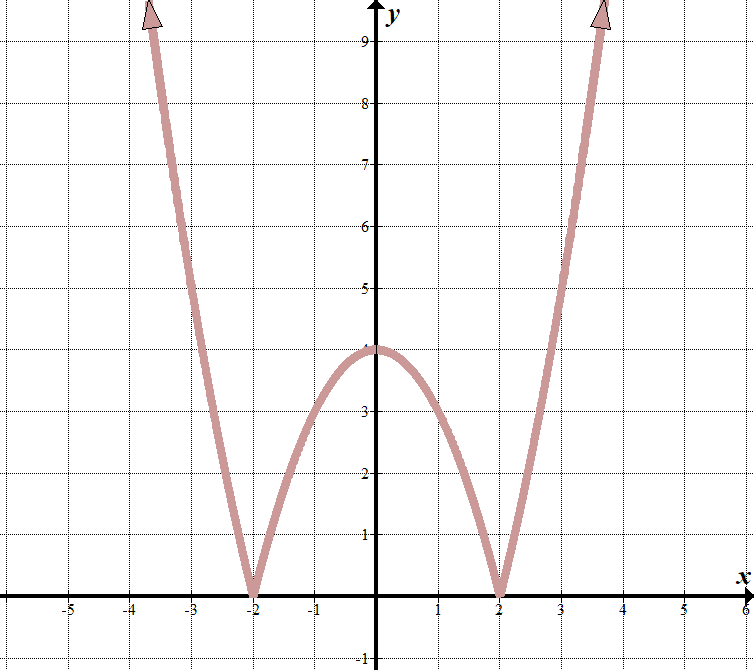 |
vi ser att våra ”gränslinjer” är på \(x=2\) och \(x=-2\), så vad är inne i absolutvärdet tecknet måste ha faktorer av \(x-2\) och \(x+2\).
När \(x< -2\) eller \(x > 2\) kan vi se att grafen ser ut som den normala delen av grafen \(y={{x}^{2}}-4\). (Jag räknade ut detta genom att känna till faktorerna och ta en bra gissning!) När \(-2<x<2\) vänds ekvationen eller negeras (vänds över \(x\)-axeln). Vi kan skriva detta som en bitvis funktion: \(\displaystyle f\left (x \ right)= \ left \ {\begin{array}{l}{{x}^{2}}-4\,\,\,\,\,\,\,\,\,\text{if }x < -2 \ text{ or }x > 2\ \ – {{x}^{2}} \ text{+ 4}\,\,\,\,\,\,\text{if }-2\le x \ le 2\end{array} \ höger.\) Vi kan se att detta startade en transformerad kvadratisk funktion \(y={{x}^{2}}-4\) med ett absolut värde runt det, eftersom alla \(y\) värden är positiva: \(y=\vänster| {{{x}^{2}}-4} \höger|\). |
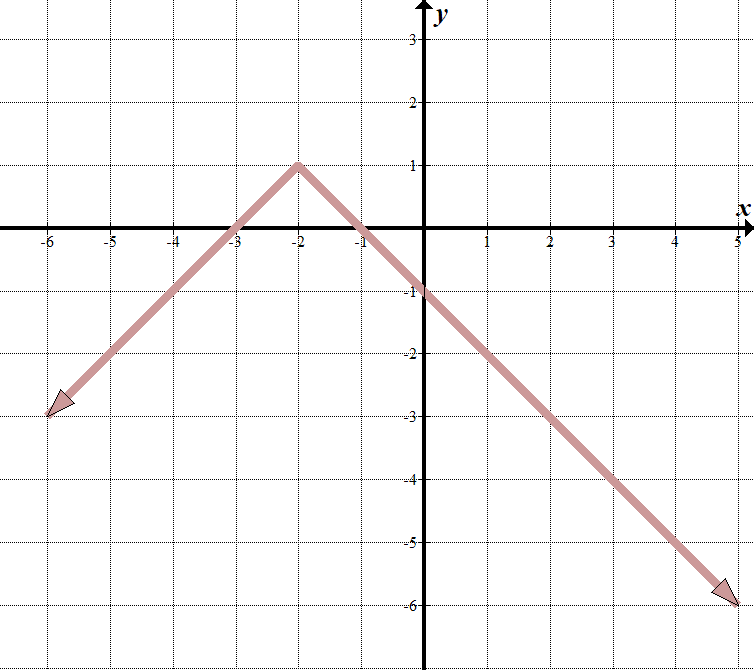 |
vi ser att vår” gränslinje ” är vid \(x=-2\), så vad som finns inuti absolutvärdet måste vara \(x+2\).
När \(x >-2\) kan vi se att ekvationen för linjen är \(y=-x-1\). När \(x<-2\) är raden \(y=x+3\). Vi kan skriva detta som en bitvis funktion: \(\displaystyle f\left (x \ right)= \ left \ {\begin{array}{l} – x-1\,\,\,\,\,\,\text{if }x > -2\ \ x+3\,\,\,\,\,\,\,\,\,\,\text{if }x \ le -2\end{array} \ höger.\ ) det är förmodligen lättare att skriva detta som en transformerad absolutvärdesfunktion. Vi kan se att den överordnade absoluta värdefunktionen vänds vertikalt, flytta till vänster 2 och upp 1. Vår absoluta värdeekvation är \(y= – \ left / {x + 2} \ right|\,\,+\,\,1\). Detta är detsamma som den bitvis funktionen ovan. Prova det-det fungerar! |
transformationer av bitvis funktioner
låt oss göra en omvandling av en bitvis funktion. Vi lärde oss om Föräldrafunktioner och deras transformationer här i avsnittet överordnade grafer och transformationer. Du kommer förmodligen vill läsa detta avsnitt först, innan du försöker en bitvis omvandling.
låt oss omvandla följande bitvis funktion vänd runt\(x\)-axeln, vertikalt sträckt med en faktor på 2 enheter, 1 enhet till höger och 3 enheter uppåt.
vi ritar \(- 2F \ vänster (x – 1 \ höger) + 3\), där:
\(\displaystyle f\vänster( x \höger)=\vänster\{ \begin{align}x+4\,\,\,\,\,\,\,\,& \ text{ if }x<& \ text{ if 1} \ le x <4 \ \ x-5\,\,\,\,\,\,\,\,& \text{ if }x\ge 4\end{align} \right.\ )
Låt oss se till att vi använder ”gränspunkterna” när vi fyller i t-diagrammet för transformationen. Kom ihåg att transformationerna inom parenteserna görs till \(x\) (gör motsatt matematik) och utanför görs till \(y\). För att komma med ett t-diagram, som visas i tabellen nedan, kan vi använda nyckelpunkter, inklusive två punkter på var och en av ”gränslinjerna”.
Observera att eftersom denna omvandling är komplicerad kan vi komma med en ny bitvis funktion genom att omvandla de 3 ”bitarna” och även omvandla ”\(x\)”s där gränspunkterna är (lägger till 1 eller går till höger 1), eftersom vi gör motsatt matematik för ”\(x\)”s. För att få de nya funktionerna i varje intervall kan vi bara ersätta ”\(x-1\)” för ”\(x\)” i den ursprungliga ekvationen, multiplicera med -2 och lägg sedan till 3. Till exempel \(\displaystyle-2F\vänster( {x-1} \höger)+3=-2\vänster+3=-2\vänster( {x+3} \höger)+3=-2x-3\).
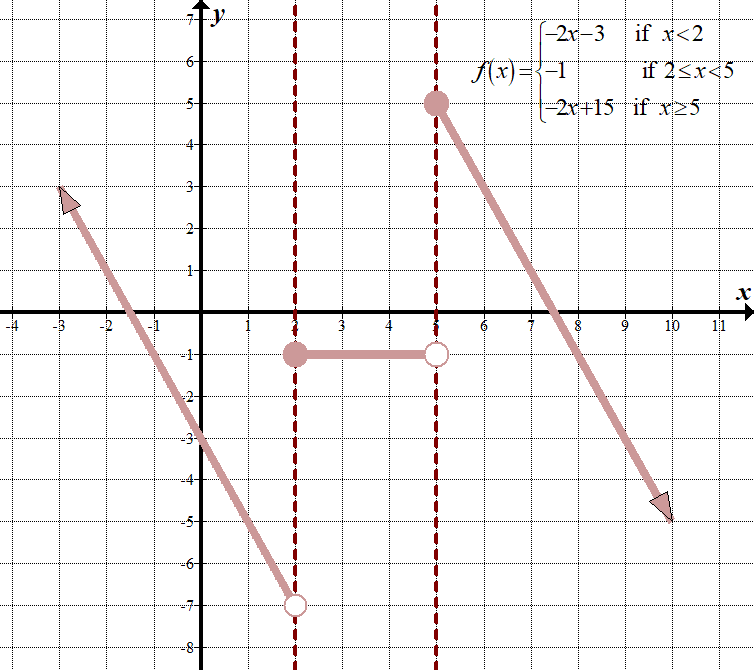
\(\displaystyle-2F \ vänster ({x-1} \ höger) + 3= \ vänster \{\begin{array}{l}-2\vänster( {\vänster ({x-1} \höger) + 4} \ Höger) + 3 = – 2x-3,\,\,\,\,\text{ if }x-1<1\,\,\,\vänster( {x< 2} \ höger)\\-2 \ vänster (2 \ höger)+3=-1,\,\,\,\,\text{ if }\, \ text{ 2 } \ Le x < 5\ \ -2 \ vänster ({\vänster ({x-1} \ höger)-5} \ höger)+3=-2x+15,\,\,\,\,\text{ if }x \ ge 5\end{array} \ höger.\ )
här är graferna” före ”och” efter”, inklusive t-diagrammet:
| Piecewise Parent Function | T-chart | Transformation of Function | ||||||||||||||||||||||||||||||||||||||||
| \(\displaystyle f\left( x \right)=\left\{ \begin{array}{l}x+4\,\,\,\,\,\,\,\,\text{if }x<1\\2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 1 }\le x<4\\x-5\,\,\,\,\,\,\,\,\text{if }x\ge 4\end{array} \right.\)
|
|
\(\displaystyle -2f\left( {x-1} \right)+3=\left\{ \begin{array}{l}-2x-3\,\,\,\,\,\,\,\,\,\text{if }x<2\\-1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if 2}\le x<5\\-2x+15\,\,\,\,\,\,\text{if }x\ge 5\end{array} \right.\)
|
||||||||||||||||||||||||||||||||||||||||
Piecewise Function Word Problems
 Problem:
Problem:
din favorit hund groomer avgifter enligt din hunds vikt. Om din hund är 15 pund och under, groomer avgifter $35. Om din hund är mellan 15 och 40 pounds, hon avgifter $40. Om din hund är över 40 pounds, hon avgifter $40, plus ytterligare $2 för varje pund.
(a) Skriv en bitvis funktion som beskriver vad din hund groomer laddar.
(b) Graf funktionen.
(c) Vad skulle groomer laddning om din söta hund väger 60 pounds?
lösning:
(A) Vi ser att ”gränspunkterna” är 15 och 40, eftersom det här är vikterna där priserna ändras. Eftersom vi har två gränspunkter har vi tre ekvationer i vår bitvis funktion. Vi måste börja vid 0, eftersom hundar måste väga över 0 Pund:
\(\displaystyle f \ vänster (x \ höger)= \ vänster \ {\begin{array}{l}\text{ }……\,\,\,\,\,\,\,\,\,\text{if }0 < X\le 15\\ \ text{ }……\,\,\,\,\,\,\,\,\,\text{if }15 < X\le 40\\ \ text{ }……\,\,\,\,\,\,\,\,\,\text{if }x>40\end{array} \right.\)
vi letar efter ”svaren” (hur mycket grooming kostar) på ”frågorna” (hur mycket hunden väger) för de tre prisintervallen. De två första är bara platta avgifter ($35 respektive $40). Den sista ekvationen är lite svårare; groomer debiterar $40 plus $2 för varje pund över 40. Låt oss prova reella tal: om din hund väger 60 pund, debiterar hon $40 plus $2 gånger \(20(60-40)\). Vi förvandlar detta till en ekvation: \(40+2(x–40)\), vilket förenklar till \(2x–40\) (se hur 2 är lutningen?).
hela bitvis funktionen är:
\(\displaystyle f \ vänster (x \ höger)= \ vänster \ {\begin{array}{l}\text{ }35\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if }0 < X\le 15\\ \ text{ }40\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if }15< x \ le 40 \ \ \ text{ }40 + 2 \ vänster ({x-40} \ höger)\,\,\,\,\,\,\text{if }x>40\end{array} \right.\ ) eller \(\displaystyle f \ left (x \right)= \ left\ {\begin{array}{l}\text{ }35\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if }0 < X\le 15\\ \ text{ }40\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if }15 < x \ le 40 \ \ \ text{ }2x-40\,\,\,\,\,\,\,\text{if }x>40\end{array} \right.\)
(b) låt oss graf: Observera att denna bitvis ekvation är icke-kontinuerlig. Observera också att en rimlig domän för detta problem kan vara \(\left ({0,200}\ right]\) (givna hundar väger inte över 200 pund!) och ett rimligt intervall kan vara \(\left \cup\left\).
Observera att denna bitvis ekvation är icke-kontinuerlig. Observera också att en rimlig domän för detta problem kan vara \(\left ({0,200}\ right]\) (givna hundar väger inte över 200 pund!) och ett rimligt intervall kan vara \(\left \cup\left\).
(c) om din hund väger 60 pund kan vi antingen använda grafen eller funktionen för att se att du måste betala $80. Whoa! Det kostar mer än en mänsklig frisyr (åtminstone mina hårklippningar)!
Problem:
du planerar att sälja hon älskar Math T-shirts som en fundraiser. Wholesale T-shirt company debiterar dig $10 en skjorta för de första 75 skjortorna. Efter de första 75 skjortorna du köper upp till 150 skjortor kommer företaget att sänka priset till $7,50 per skjorta. När du har köpt 150 skjortor kommer priset att minska till $ 5 per skjorta. Skriv en funktion som modellerar denna situation.
lösning:
vi ser att ”gränspunkterna” är 75 och 150, eftersom det här är antalet T-shirts som köps där priserna ändras. Eftersom vi har två gränspunkter har vi tre ekvationer i vår bitvis funktion. Vi börjar med \(x \ ge 1\), eftersom vi antar att minst en skjorta är köpt. I det här problemet måste antalet köpta T-shirts (\(x\)) eller domänen vara ett heltal, men denna begränsning bör inte påverka resultatet av problemet.
\(\displaystyle f\vänster( x \höger)=\vänster\{ \begin{array}{l}\text{ }……\text{ if }1\le x\le 75\\\text{ }……\text{ if }75<x\le 150\\\text{ }……\text{ if }x>150\end{array} \right.\)
vi letar efter ”svar” (total kostnad för t-shirts) till ”frågor” (hur många köps) för de tre prisintervallen.
för upp till och med 75 skjortor är priset $10, så det totala priset skulle \(10x\). För mer än 75 skjortor men upp till 100 skjortor är kostnaden $7,50, men de första 75 t-tröjorna kostar fortfarande $10 per skjorta. Den andra funktionen inkluderar $750 som spenderas på de första 75 skjortorna (75 gånger $10) och inkluderar också $7,50 gånger antalet skjortor över 75, vilket skulle vara \((x-75)\). Om du till exempel köpte 80 skjortor måste du spendera \(\$10 \ gånger 75= \ $750\), plus \(\$7.50\gånger 5\,\) (80 – 75) för skjortorna efter den 75: e skjortan.
på samma sätt, för över 150 skjortor, skulle vi fortfarande betala $10-priset upp genom 75-skjortor, $7.50 pris för 76 till 150 skjortor (75 fler skjortor), och sedan $5 per skjorta för antalet skjortor köpte över 150. Vi betalar \(10(75)+7.50(75)+5(x-150)\) för\ (x\) skjortor. Sätt i siffror och prova det!
hela bitvis funktionen är:
\(\displaystyle f \ left (x \right)= \ left \ {\begin{array}{l} \ text{ }10x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if }1 \ le x \ le 75 \ \ \ text{ }7,5 x \ text { } + \ text{ }187.5\,\,\,\,\,\text{if 7}5<x\le 150\\\text{ }5x+562.5\,\,\,\,\,\,\,\,\,\,\text{ if }x>150\end{array} \right.\ ) eller \(\displaystyle f \ left (x \right)= \ left\ {\begin{array}{l} \ text{ }10x\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if }1 \ le x \ le 75 \ \ \ text{ }7,5 x \ text { } + \ text{ }187.5\,\,\,\,\,\text{if 7}5< x \ le 150 \ \ \ text{ }5x+562.5\,\,\,\,\,\,\,\,\,\,\,\text{if }x>150\end{array} \right.\ )
Problem:
en buss kostar $50 för de första 400 milen, och varje ytterligare 300 miles (eller en bråkdel därav) lägger till $10 till priset.
använd en bitvis funktion för att representera busspriset när det gäller avståndet i miles.
lösning:
detta är faktiskt ett knepigt problem, men låt oss först tänka först om ”gränspunkten”, som är 400. Det är ganska enkelt när resan är mindre än 400 miles; kostnaden är $50.
för större än 400 miles måste vi subtrahera de första 400 milen (men kom ihåg att inkludera de första $50), dela antalet mil kvar med 300 miles (och runda upp, om det finns ett bråkbelopp) och multiplicera det med $10.
den knepiga delen är när vi ”runda upp” för en del av de närmaste 300 milen. Vi kan använda en” tak ” – funktion (betecknad med \(\left \lceil {}\right \ rceil\)); denna funktion ger det minsta heltalet som är större än eller lika med dess ingång; till exempel är taket på både 3,5 och 4 4.
det här är vad vi har:
\(\displaystyle f \ vänster (x \ höger)= \ vänster \ {\begin{array}{l} \ text{ }50 \ text{ }\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\text{if }0 \ le x \ le 400 \ \ \ text{ }50+10\gånger \ vänster \ lceil {\frac {{x-400}}{{300}}} \höger \ rceil \ text{ }\,\,\,\,\,\,\text{ if }x>400\end{array} \right.\ )
låt oss prova det! Om vi har en 1500 mil lång resa skulle kostnaden vara \(\displaystyle 50+10 \times\left\lceil {\frac{{1500-400}}{{300}}} \höger\rceil \ text { } = 50+10 \ gånger 4= \ $90\).
Problem:
vilket värde av \(\boldsymbol{a}\) skulle göra denna bitvis funktion kontinuerlig?
\(\displaystyle f \ vänster (x \ höger)= \ vänster \ {\begin{array}{l}3{{x}^{2}}+4\,\,\,\,\,\text{ if }x < -2\ \ 5x + \ boldsymbol{a}\,\,\,\,\,\,\,\,\text{if }x \ ge -2\end{array} \höger.\)
lösning:
för att funktionen ska vara kontinuerlig måste de två\ (y\) värdena vara desamma vid gränspunkten(där funktionen ändras). Vi kan ansluta -2 för \(x\) i båda funktionerna och se till att \(y\) är samma
\(\begin{align}3{{x}^{2}}+4&=5x+a\\3{{\left ({-2} \ right)}^{2}}+4&=5\vänster( {-2} \höger)+a\\12+4&=-10+a\\a&=26\end{align}\)
Om \(a=26\) är funktionen bitvis fortlöpande!
lär dig dessa Regler och öva, öva, öva!
mer övning: använd Mathway-widgeten nedan för att försöka skriva en bitvis funktion. Klicka på skicka (den blå pilen till höger om problemet) och klicka på Skriv det absoluta värdet som bitvis för att se svaret.
Du kan också skriva in ditt eget problem, eller klicka på de tre punkterna i det övre högra hörnet och klicka på ”exempel” för att borra ner efter ämne.
Om du klickar på tryck för att visa steg, eller klicka här, kan du registrera dig på Mathway för en gratis provperiod, och sedan uppgradera till en betald prenumeration när som helst (för att få någon typ av matematik problem löst!).
vidare till matriser och Lösningssystem med matriser – du är redo!