Efter att ha förstått den exponentiella funktionen är vårt nästa mål den naturliga logaritmen.

Med tanke på hur den naturliga loggen beskrivs i matematiska böcker finns det lite ”naturligt” om det: det definieras som inversen av $e^x$, en konstig nog exponent redan.

men det finns en ny, intuitiv förklaring: den naturliga loggen ger dig den tid som behövs för att nå en viss tillväxtnivå.

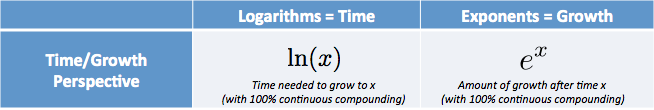
Antag att du har en investering i gummy bears (vem gör det inte?) med en ränta på 100% per år, växer kontinuerligt. Om du vill ha 10x tillväxt, förutsatt kontinuerlig sammansättning, väntar du bara $ \ ln (10)$ eller 2.302 år. Förstår du inte varför det bara tar några år att få 10x tillväxt? Ser du inte varför mönstret inte är 1, 2, 4, 8? Läs mer om e.

e och den naturliga loggen är tvillingar:

• $e^x$ är det belopp Vi har efter att ha startat vid 1.0 och växer kontinuerligt för $x$ tidsenheter
• $\ln (x)$ (naturlig logaritm) är tiden att nå belopp $x$, förutsatt att vi växte kontinuerligt från 1.0

inte så illa, eller hur? Medan matematikerna scramble för att ge dig den långa, tekniska förklaringen, låt oss dyka in i den intuitiva.

E handlar om tillväxt

antalet e handlar om kontinuerlig tillväxt. Som vi såg förra gången låter $E^x$ oss sammanfoga takt och tid: 3 år vid 100% tillväxt är densamma som 1 år vid 300% tillväxt, när den kontinuerligt förvärras.

Vi kan ta en kombination av hastighet och tid (50% i 4 år) och konvertera kursen till 100% för bekvämlighet (ger oss 100% i 2 år). Genom att konvertera till en hastighet på 100% behöver vi bara tänka på tidskomponenten:

intuitivt betyder $e^x$:

• hur mycket tillväxt får jag efter efter X tidsenheter (och 100% kontinuerlig tillväxt)
• till exempel: efter 3 tidsperioder har jag $e^3$ = 20.08 gånger mängden ”saker”.

$e^x$ är en skalningsfaktor som visar oss hur mycket tillväxt vi skulle få efter $x$ tidsenheter.

naturlig logg handlar om tiden

den naturliga loggen är inversen av $e^x$, en snygg term för motsatt. På tal om fantasi är det latinska namnet logarithmus naturali, vilket ger förkortningen ln.

vad betyder detta omvända eller motsatta saker?

• $e^x$ låter oss koppla in tid och få tillväxt.
• $\ln (x)$ låter oss koppla in tillväxt och få den tid det skulle ta.

till exempel:

• $e^3$ är 20,08. Efter 3 tidsenheter slutar vi med 20.08 gånger vad vi började med.
• $\ln (20.08)$ handlar om 3. Om vi vill ha tillväxt på 20.08, skulle vi vänta 3 tidsenheter (igen, förutsatt en 100% kontinuerlig tillväxttakt).

med mig? Den naturliga loggen ger oss den tid som behövs för att nå vår önskade tillväxt.

logaritmisk aritmetik är inte normalt

Du har studerat loggar tidigare, och de var konstiga djur. Hur gjorde de multiplikation till Tillägg? Uppdelning i subtraktion? Låt oss se.

vad är $ \ ln (1)$? Intuitivt är frågan: Hur länge väntar jag på att få 1x mitt nuvarande belopp?

noll. Zip. Nada. Du är redan på 1x ditt nuvarande belopp! Det tar ingen tid att växa från 1 till 1.

• $\ln(1) = 0$

Ok, vad sägs om ett fraktionsvärde? Hur länge får jag 1/2 mitt nuvarande belopp? Förutsatt att du växer kontinuerligt med 100% vet vi att $\ln(2)$ är tiden att fördubbla. Om vi vänder det (dvs tar den negativa tiden) skulle vi ha hälften av vårt nuvarande värde.

• $\ln(.5) = – \ln(2)= -.693$

är vettigt, eller hur? Om vi går bakåt .693 enheter (negativa sekunder, låt oss säga) vi skulle ha hälften av vårt nuvarande belopp. I allmänhet kan du vända fraktionen och ta det negativa: $\ln(1/3) = – \ln(3) = -1.09$. Det betyder att om vi går tillbaka 1,09 tidsenheter, skulle vi ha en tredjedel av vad vi har nu.

Ok, vad sägs om den naturliga loggen för ett negativt tal? Hur mycket tid tar det att ”växa” din bakteriekoloni från 1 till -3?

det är omöjligt! Du kan inte ha en ”negativ” mängd bakterier, eller hur? Högst (er… minst) kan du ha noll, men det finns inget sätt att ha en negativ mängd små critters. Negativa bakterier är bara inte meningsfulla.

• $\ln(\text{negative number}) = \text{undefined}$

Undefined betyder bara ”det finns ingen tid du kan vänta” för att få ett negativt belopp. (Tja, om vi använder imaginära exponentialer finns det en lösning. Men idag ska vi hålla det riktigt.)

logaritmisk multiplikation är mäktig kul

hur lång tid tar det att växa 9x ditt nuvarande belopp? Visst, vi kan bara använda ln (9). Men det är för lätt, låt oss vara annorlunda.

Vi kan överväga 9x tillväxt som tredubbling (tar $ \ ln (3)$ tidsenheter) och sedan tredubbla igen(tar en annan $\ln (3)$ tidsenheter):

• tid att växa 9x = $\ln (9)$ = tid att trippel och trippel igen = $\ln(3) + \ln(3)$

intressant. Varje tillväxtnummer, som 20, kan betraktas som 2x tillväxt följt av 10X tillväxt. Eller 4x tillväxt följt av 5x tillväxt. Eller 3x tillväxt följt av 6.666 X tillväxt. Ser du mönstret?

• $\ln (a * b) = \ln(a) + \ln(b)$

loggen för a gånger b = log(a) + log(b). Detta förhållande är vettigt när du tänker när det gäller tid att växa.

Om vi vill växa 30x kan vi vänta $ \ ln(30)$ på en gång, eller helt enkelt vänta $\ln(3)$, till trippel, vänta sedan $\ln(10)$, för att växa 10x igen. Nettoeffekten är densamma, så nettotiden bör också vara densamma (och det är).

vad sägs om division? $ \ ln (5/3)$ betyder: hur lång tid tar det att växa 5 gånger och sedan ta 1/3 av det?

Tja, växer 5 gånger är $ \ ln (5)$. Växande 1/3 är $ – \ln (3)$ tidsenheter. Så

• $\ln (5/3) = \ln(5) – \ln(3)$

som säger: växa 5 gånger och ”gå tillbaka i tiden” tills du har en tredjedel av det beloppet, så du är kvar med 5/3 tillväxt. I allmänhet har vi

• $\ln (a / b) = \ln (a) – \ln (b)$

Jag hoppas att logaritmernas konstiga matematik börjar vara meningsfull: multiplikation av tillväxt blir tillägg av tid, uppdelning av tillväxt blir subtraktion av tid. Memorera inte reglerna, förstå dem.

använda naturliga loggar med någon hastighet

”visst,” säger du, ” det här loggmaterialet fungerar för 100% tillväxt men hur är det med de 5% jag normalt får?”

det är inget problem. Den ” tid ” vi kommer tillbaka från $\ln ()$ är faktiskt en kombination av hastighet och tid, ”x” från vår $e^x$ ekvation. Vi antar bara 100% för att göra det enkelt, men vi kan använda andra nummer.

Antag att vi vill ha 30x tillväxt: Anslut $\ln(30)$ och få 3.4. Detta innebär:

• $e^x = \ text{tillväxt}$
• $e^{3.4} = 30$

och intuitivt betyder denna ekvation ”100% avkastning för 3.4 år är 30x tillväxt”. Vi kan betrakta ekvationen som:

vi kan ändra ”rate” och ”time”, så länge som rate * time = 3.4. Anta till exempel att vi vill ha 30x tillväxt — hur länge väntar vi på 5% avkastning?

• $\ln (30) = 3,4$
• $\text{rate} * \text{time} = 3.4$
• $.05 * \text{time} = 3.4$
• $ \ text{time} = 3.4/.05 = 68 \text{years}$

intuitivt tror jag ” $\ln(30) = 3.4$, så vid 100% tillväxt tar det 3.4 år. Om jag fördubblar tillväxttakten halverar jag den tid som behövs.”

• 100% för 3,4 år = 1,0 * 3,4 = 3,4
• 200% för 1,7 år = 2,0 * 1,7 = 3,4
• 50% för 6,8 år = 0,5 * 6,8 = 3,4
• 5% för 68 år = .05 * 68 = 3.4

Cool, va? Den naturliga loggen kan användas med någon ränta eller tid så länge deras produkt är densamma. Du kan vinkla variablerna allt du vill.

fantastiskt exempel: regeln om 72

regeln om 72 är en mental matematisk genväg för att uppskatta den tid som behövs för att fördubbla dina pengar. Vi kommer att härleda det (yay!) och ännu bättre, vi kommer att förstå det intuitivt.

hur lång tid tar det att dubbla dina pengar till 100% ränta, förvärras varje år?

Uh oh. Vi har använt natural log för kontinuerliga priser, men nu ber du om årlig ränta? Kommer det inte att förstöra vår formel? Ja, det kommer, men till rimliga räntor som 5%, 6% eller till och med 15% är det inte mycket skillnad mellan årlig sammansatt och helt kontinuerlig ränta. Så den grova formeln fungerar, uh, grovt och vi låtsas att vi får helt kontinuerligt intresse.

nu är frågan lätt: Hur lång tid att dubbla med 100% ränta? ln (2)=.693. Det krävs .693 tidsenheter (år, i detta fall) för att fördubbla dina pengar med kontinuerlig sammansättning med en hastighet på 100%.

Ok, vad händer om vårt intresse inte är 100% Vad händer om det är 5% eller 10%?

enkelt. Så länge som hastighet * tid = .693, vi fördubblar våra pengar:

• rate * time = .693
• tid = .693 / rate

Så, om vi bara hade 10% tillväxt, skulle det ta .693 / .10 eller 6,93 år att fördubbla.

för att förenkla saker, låt oss multiplicera med 100 så att vi kan prata om 10 snarare än .10:

• tid till dubbel = 69,3/hastighet, där hastigheten antas vara i procent.

nu är tiden att fördubbla vid 5% tillväxt 69,3 / 5 eller 13,86 år. 69,3 är dock inte det mest delbara numret. Låt oss välja en nära granne, 72, som kan delas med 2, 3, 4, 6, 8 och många fler nummer.

• time to double = 72/rate

vilket är regeln om 72! Lätt breezy.

Om du vill hitta tiden att tredubbla, skulle du använda ln (3) ~ 109.8 och få

• tid att trippel = 110 / rate

vilket är en annan användbar tumregel. Regeln om 72 är användbar för räntor, befolkningstillväxt, bakteriekulturer och allt som växer exponentiellt.

var ska man härifrån?

Jag hoppas att den naturliga loggen är mer meningsfull – den berättar den tid som behövs för någon mängd exponentiell tillväxt. Jag anser att det är ”naturligt” eftersom e är den universella tillväxttakten, så ln kan betraktas som det ”universella” sättet att ta reda på hur lång tid det tar att växa.

När du ser $\ln (x)$, tänk bara ”hur mycket tid att växa till x”. I nästa artikel kommer vi att föra e och ln tillsammans, och den söta doften av matematik kommer att fylla luften.

bilaga: den naturliga loggen för e

Snabbquiz: Vad är $\ln(e)$?

• matematikroboten säger: eftersom de definieras som inversa funktioner, klart $\ln(e) = 1$
• den intuitiva människan: ln (e) är den tid det tar att få ”e” tillväxtenheter (ca 2.718). Men e är mängden tillväxt efter 1 tidsenhet, så $\ln (e) = 1$.

Tänk intuitivt.

andra inlägg i denna serie

1. en intuitiv Guide till exponentiella funktioner & e
2. avmystifiera den naturliga logaritmen (ln)
3. en visuell Guide till enkla, sammansatta och kontinuerliga räntor
4. gemensamma definitioner av e (Colorized)
5. förstå exponenter (Varför gör 0^0 = 1?)
6. använda logaritmer i den verkliga världen
7. hur man tänker med exponenter och logaritmer
8. förstå diskret vs kontinuerlig tillväxt
9. Vad betyder en exponent egentligen?
10. Q: Varför är e speciell? (2.718…, inte 2, 3.7 eller ett annat nummer?)