i andra avsnitt nämndes att många av egenskaperna hos fasta ämnen, vätskor och gaser kunde redovisas om vi antog att ämnen är gjorda av atomer eller molekyler som ständigt är i rörelse. Boyles lag och de andra gaslagarna har nu gett oss mycket mer kvantitativ information om gaser, och det är värt att fråga om vi med den tidigare modellen kan göra kvantitativa förutsägelser i överensstämmelse med dessa lagar. När vi besvarar denna fråga kommer vi också att få viktiga insikter i temperaturens och värmeenergins natur.

den mikroskopiska teorin om gasbeteende baserat på molekylär rörelse kallas kinetisk teori om gaser. Dess grundläggande postulat listas i Tabell 1:

tabell \(\PageIndex{1}\) postulat av kinetisk teori om gaser.

1 molekylerna i en gas är små och mycket långt ifrån varandra. Det mesta av volymen som en gas upptar är tomt utrymme.

2 gasmolekyler är i konstant slumpmässig rörelse. Lika många molekyler rör sig i en riktning som i någon annan.

3 molekyler kan kollidera med varandra och med behållarens väggar. Kollisioner med väggarna står för gasens tryck.

4 när kollisioner inträffar förlorar molekylerna ingen kinetisk energi; det vill säga kollisionerna sägs vara helt elastiska. Den totala kinetiska energin hos alla molekyler förblir konstant om det inte finns någon yttre störning med

5 molekylerna utövar inga attraktiva eller repulsiva krafter på varandra utom under kollisionsprocessen. Mellan kollisioner rör de sig i raka linjer.

från dem är det möjligt att härleda följande uttryck för trycket hos en gas i termer av egenskaperna hos dess molekyler:

\ där P, V = tryck och volym av gasen

N = antal molekyler

M = massa av varje molekyl

(u2)ave = medelvärde (eller medelvärde) av kvadraterna för alla individuella molekylhastigheter. Denna genomsnittliga kvadrathastighet måste användas eftersom trycket är proportionellt mot kvadraten av molekylhastighet, och molekylära kollisioner orsakar olika molekyler att ha helt olika hastigheter.

snarare än om oss själva med förfarandet för att härleda Eq. \(\ref{1}\), Låt oss inspektera ekvationen och se att dess allmänna egenskaper är mycket som vi förväntar oss. På vissa sätt är förmågan att göra detta med en formel Mer användbar än förmågan att härleda den. Figur \(\PageIndex{1}\)

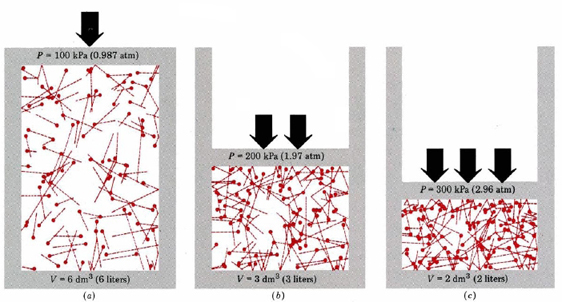först och främst berättar ekvationen att trycket på en gas är proportionellt mot antalet molekyler dividerat med volymen. Detta visas grafiskt i Figur \(\PageIndex{1}\), där en dator har ritat samma antal gasmolekyler som upptar var och en av tre olika volymer. ”Svansen” på varje molekyl visar den exakta vägen följt av den molekylen i föregående mikrosekund—ju längre svansen desto snabbare gick molekylen. Medelvärdet av kvadraterna på svanslängderna är proportionellt mot (u2)Ave och är detsamma i alla tre diagrammen. Det antas också att alla molekyler har lika massor.

som du kan se ökar gasvolymen antalet kollisioner per enhetsarea på behållarens väggar. Varje kollision utövar kraft på väggen; kraft per ytenhet är tryck, och så är antalet kollisioner per ytenhet proportionellt mot tryck. Att halvera volymen fördubblar trycket, en förutsägelse som överensstämmer med de experimentella fakta som sammanfattas i Boyles lag. Ekvation \(\ref{1}\) säger också att trycket är proportionellt mot massan för varje gasmolekyl. Återigen är det vad vi förväntar oss. Tunga molekyler ger en större ”push”(den tekniska termen för detta är impuls) mot väggen än lätta med samma hastighet.

slutligen berättar ekvationen att trycket är proportionellt mot medelvärdet av kvadraterna för molekylhastigheterna. Detta beroende av hastighetstorget är rimligt om vi inser att fördubbling av hastigheten hos en molekyl har två effekter.

först kan molekylen röra sig längre under en viss tid, vilket fördubblar antalet kollisioner med väggarna. Detta skulle fördubbla trycket. För det andra fördubblar hastigheten hos en molekyl trycket eller impulsen för varje kollision. Detta fördubblar trycket igen. Därför fördubblas en molekyls hastighet fyrdubblar trycket, och för ett stort antal molekyler är P proportionell mot medelkvadrathastigheten.