Boyles lag
Robert Boyle (1627 – 1691), en engelsk kemist, anses allmänt vara en av grundarna av den moderna experimentella vetenskapen om kemi. Han upptäckte att fördubbling av trycket i ett slutet gasprov samtidigt som temperaturen var konstant orsakade att gasvolymen minskade med hälften. Boyles lag säger att volymen av en given gasmassa varierar omvänt med trycket när temperaturen hålls konstant. Ett omvänt förhållande beskrivs på detta sätt. När en variabel ökar i värde minskar den andra variabeln.
fysiskt, vad händer? Gasmolekylerna rör sig och är ett visst avstånd från varandra. En ökning av trycket pressar molekylerna närmare varandra, vilket minskar volymen. Om trycket minskar är gaserna fria att röra sig i en större volym.

matematiskt kan Boyles lag uttryckas med ekvationen:
\
\(k\) är en konstant för ett givet gasprov och beror endast på gasens massa och temperaturen. Tabellen nedan visar tryck-och volymdata för en viss mängd gas vid en konstant temperatur. Den tredje kolumnen representerar värdet på konstanten \(\vänster (k \höger)\) för dessa data och är alltid lika med trycket multiplicerat med volymen. När en av variablerna ändras ändras den andra på ett sådant sätt att produkten av \(P \times V\) alltid förblir densamma. I det här fallet är den konstanten \(500 \: \text{atm} \cdot \text{mL}\).
| Pressure \(\left( \text{atm} \right)\) | Volume \(\left( \text{mL} \right)\) | \(P \times V = k\) \(\left( \text{atm} \cdot \text{mL} \right)\) |
|---|---|---|
| 0.5 | 1000 | 500 |
| 0.625 | 800 | 500 |
| 1.0 | 500 | 500 |
| 2.0 | 250 | 500 |
| 5.0 | 100 | 500 |
| 8.0 | 62.5 | 500 |
| 10.0 | 50 | 500 |
en graf över data i tabellen ytterligare illustrerar den omvända relationen karaktären av Boyles lag (se figur nedan). Volymen är ritad på\(x\)-axeln, med motsvarande tryck på\(y\)-axeln.
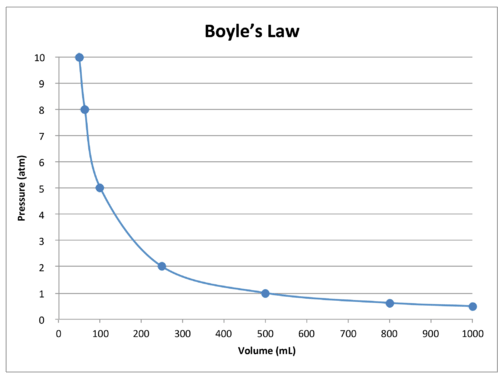
Boyles lag kan användas för att jämföra förändrade förhållanden för en gas. Vi använder \(P_1\) och \(V_1\) för att stå för initialtrycket och initialvolymen för en gas. När en ändring har gjorts står \(P_2\) och \(V_2\) för det slutliga trycket och volymen. Det matematiska förhållandet mellan Boyles lag blir:
\
denna ekvation kan användas för att beräkna någon av de fyra kvantiteterna om de andra tre är kända.
exempel \(\PageIndex{1}\)
ett prov av syrgas har en volym av \(425 \: \text{mL}\) när trycket är lika med \(387 \: \text{kPa}\). Gasen får expandera till en \ (1.75\:\ text{L}\) Behållare. Beräkna det nya trycket på gasen.
lösning
Steg 1: Lista de kända kvantiteterna och planera problemet.
känd
- \(P_1 = 387 \: \text{kPa}\)
- \(V_1 = 425 \: \text{mL}\)
- \(V_2 = 1.75 \: \text{L} = 1750 \: \text{mL}\)
okänd
- \(p_2 = ? \ : \ text{kPa}\)
använd Boyles lag för att lösa för det okända trycket \(\vänster (P_2\höger)\). Det är viktigt att de två volymerna (\(V_1\) och \(V_2\)) uttrycks i samma enheter, så \(V_2\) har konverterats till \(\text{mL}\).
steg 2: Lös.
ordna först ekvationen algebraiskt för att lösa för \(P_2\).
\
ersätt nu de kända kvantiteterna i ekvationen och lösa.
\
steg 3: Tänk på ditt resultat.
volymen har ökat till något över 4 gånger sitt ursprungliga värde och så minskar trycket med ungefär en fjärdedel. Trycket är i \(\text{kPa}\) och värdet har tre signifikanta siffror. Observera att alla tryck-eller volymenheter kan användas så länge de är konsekventa under hela problemet.